基于ALCE⁃SSA优化的三维无人机低空突防

doi:10.13232/j.cnki.jnju.2022.03.009

基于ALCE⁃SSA优化的三维无人机低空突防

黄鹤¹^,², 李文龙¹^,², 吴琨¹^,², 王会峰¹, 茹锋¹^,², 王珺^,¹

1.西安市智慧高速公路信息融合与控制重点实验室, 长安大学, 西安, 710064

2.长安大学电子与控制工程学院, 西安, 710064

3D UAV low altitude penetration optimization based on ALCE⁃SSA

Huang He¹^,², Li Wenlong¹^,², Wu Kun¹^,², Wang Huifeng¹, Ru Feng¹^,², Wang Jun^,¹

1.School of Electronics and Control Engineering, Chang'an University，Xi'an，710064，China

2.Xi'an Key Laboratory of Intelligent Expressway Information Fusion and Control，Xi'an，710064，China

通讯作者: E⁃mail：jwang@nwu.edu.cn

收稿日期: 2022-01-22

基金资助:

国家自然科学基金.  52172324
国家重点研发计划.  2021YF2501200
陕西省重点研发计划.  2021SF⁃483
陕西省自然科学基础研究计划.  2021JM⁃184
西安市智慧高速公路信息融合与控制重点实验室（长安大学）开放基金.  300102321502

Received: 2022-01-22

摘要

针对无人机在三维低空突防时存在环境复杂、路径规划计算量大等问题以及现有的麻雀搜索算法算法路径搜索能力不足、易陷入局部最优等缺陷，提出一种基于改进麻雀搜索算法（ALCE⁃SSA）的三维无人机低空突防的航迹规划方法.首先，建立三维地形模型、威胁源模型和无人机物理约束模型，确定代价函数；其次，设计随机Tent映射初始化种群，提高初始化种群的质量；然后针对麻雀搜索算法算法中发现者位置更新的不足，设计一种自适应领头雀引导策略，减小依靠单一父代更新的不利影响，能够同时提升前期全局探索和后期局部寻优的能力；最后，针对种群多样性不足、易陷入局部最优的问题，设计一种中心变异⁃进化因子，扩大搜索空间，进一步提升全局寻优能力.和灰狼算法、飞蛾扑火算法和麻雀搜索算法相比，ALCE⁃SSA的能耗更优，路径更平滑，收敛速度更快，可使无人机有效地利用地形优势来躲避威胁源，表现出较好的寻优能力.

关键词： 无人机 ; 低空突防 ; 全局最优 ; 群智能算法 ; 改进麻雀搜索算法

Abstract

Aiming at the problems of complex environment and large amount of calculation in the three⁃dimensional low altitude penetration of UAV，as well as the insufficient path search ability of the existing Sparrow Search Algorithm (SSA) and easy to fall into local optimization，a path planning method for low altitude penetration of three⁃dimensional UAV based on improved SSA (ALCE⁃SSA) is proposed. Firstly，three⁃dimensional terrain model，threat source model and UAV physical constraint model are established，and the cost function is determined combined with the above model. Secondly，using random tent mapping to initialize the population，the quality of the initialized population is improved. Then，aiming at the shortcomings of the location update of the discoverer in SSA algorithm，an adaptive leader guide strategy is designed to reduce the adverse effect of relying on a single parent update，which can improve the ability of global exploration in early stage and local optimization in the later stage. Finally，aiming at the problem of insufficient population diversity and easy to fall into local optimization，a central mutation⁃evolution factor is designed to expand the search space，which furtherly improves the ability of global optimization. Compared with the Grey Wolf Optimization (GWO)，Moth⁃Flame Optimization (MFO) and SSA，ALCE⁃SSA has better energy consumption，smoother path and faster convergence speed，which enables UAV to effectively use terrain advantages to avoid threat sources and show excellent optimization ability.

Keywords： UAV ; low altitude penetration ; global optimum ; swarm intelligence algorithm ; ALCE⁃SSA

PDF (1671KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

黄鹤, 李文龙, 吴琨, 王会峰, 茹锋, 王珺. 基于ALCE⁃SSA优化的三维无人机低空突防. 南京大学学报（自然科学）[J], 2022, 58(3): 448-459 doi:10.13232/j.cnki.jnju.2022.03.009

Huang He, Li Wenlong, Wu Kun, Wang Huifeng, Ru Feng, Wang Jun. 3D UAV low altitude penetration optimization based on ALCE⁃SSA. Journal of nanjing University[J], 2022, 58(3): 448-459 doi:10.13232/j.cnki.jnju.2022.03.009

低空突防是无人机作战中的重要环节^［1-2］，也是目前的研究热点.为了找出一条从起点到终点的可以避开威胁源的安全路径，突防目标以有效的规划路线方法为基础，在约束问题下找出最优解，其关键在于寻优算法的优劣.近年来学者们展开深入研究，提出了多种低空突防路径规划算法，主要分为两大类：（1）常规算法，如人工势场法^［3］、A*算法^［4］等；（2）智能算法，如遗传算法（Genetic Algorithms，GA）^［5］、粒子群算法（Particle Swarm Optimization，PSO）^［6］、灰狼算法（Grey Wolf Optimization，GWO）^［7］、飞蛾扑火算法（Moth⁃Flame Optimization，MFO）^［8］等.和常规算法相比，智能算法收敛速度快，鲁棒性强^［9］，而采用群体智能优化算法求解无人机突防路径的问题更是目前的研究热点.张宏宏等^［10］为了解决无人机低空突防的问题，利用改进蚁群算法生成一条风险较低的路径，提升了寻优效率，但路径精确度不高.宋宇和王志明^［11］提出一种基于三维规划的改进粒子群优化方法，提升了搜索性能，但威胁场考虑得比较简单，也没有考虑地形等因素，实际应用效果不理想.许江波和刘琳岚^［12］通过自适应策略改进鱼群算法，利用其全局寻优能力解决路径规划问题，但搜索时间过长.以上研究虽然实现了无人机的航迹规划，但路径规划效果和迭代收敛速度仍有进一步改进空间.麻雀搜索算法（Sparrow Search Algorithm，SSA）是2020年由Xue and Shen^［13］提出的一种新的群智能优化算法，模拟麻雀觅食的过程，具有收敛速度快、适应性强、模型易修改等特点，适用于无人机路径规划.汤安迪等^［14］提出一种基于混沌麻雀搜索算法的航迹规划法，能够快速地得到一条安全的可行航迹，但该算法仅仅针对二维场景的应用，存在一定的局限性.SSA本身还存在易陷入局部最优、种群多样性快速减少等问题，需要进一步改进.

基于以上研究，提出一种自适应领头雀引导和中心变异⁃进化因子的麻雀搜索算法（Adaptive Leading Sparrow Guide and Center Mutation⁃evolution Factor Sparrow Search Algorithm，ALCE⁃SSA），在保证快速寻优的前提下，获得无人机突防的最优路径.

1 无人机三维突防环境建模

在处理三维环境的无人机突防问题时，为了达到快速寻优的目的，假设已通过测绘得到所有的静态环境，需要根据已知的参数将地形、威胁源构造建模，然后根据建模以及无人机自身约束求出代价总和.

1.1　地形约束

将无人机的突防环境^［15-16］分为平原和山地两种地形，其中山峰影响最大.三维环境下的山峰建模如下：

z (x, y) = h \cdot e^{{(- \frac{{(x - x_{0})}^{2}}{λ_{1}} - \frac{{(y - y_{0})}^{2}}{λ_{2}})}^{2}}

(1)

其中， $(x, y)$ 为地形的坐标， $(x_{0}, y_{0})$ 为山峰地形的中心点坐标，h为高度参数，λ₁和λ₂反映山峰的陡峭程度.在飞行中，离地面0.05~2.5 km高度处适于飞行，航迹点的地形威胁代价如下：

f_{Z, j} = \{\begin{matrix} \begin{matrix} K_{Z}^{}, & h_{j} - Z_{j} \leq 0 \end{matrix} \\ \begin{matrix} K_{Z}^{'}, & 0 \leq h_{j} - Z_{j} \leq 0.05 \end{matrix} \\ \begin{matrix} 0, & 0.05 \leq h_{j} - Z_{j} \leq 2.5 \end{matrix} \\ \begin{matrix} K_{Z}^{'}, & 2.5 \leq h_{j} - Z_{j} \end{matrix} \end{matrix}

(2)

其中 $, K_{Z}, K_{Z}^{'}$ 为地形威胁系数，h_j 为第j个航迹点的海拔高度，Z_j 为第j个航迹点的地形高度，f_Z，j 为第j个航迹点对应的威胁代价.此外，低空突防需考虑高程代价，航迹点j的高程代价如下所示：

f_{H, j} = h_{j}

(3)

地形约束还需考虑飞行边界范围和最大飞行高度，保证无人机的可控性.设定飞行水平范围为 $(x_{m i n}, y_{m i n}) = (0,0)$ 和 $(x_{m a x}, y_{m a x}) = (100,100)$ ，最大飞行高度为 $z_{m a x} = 5$ .

1.2　威胁模型约束

雷达探测、防空火炮、地空导弹等是无人机突防的主要威胁来源.地形中的威胁源建模原理是根据威胁的性质计算威胁的作用半径和作用空间形状，以等效地形来代替^［17］.具体建模如下：

(1)雷达威胁：在雷达区内，简化的雷达探测概率模型如下：

P_{0} = 1 / r^{4}

(4)

其中，r为航迹点到威胁源中心的距离.

(2)防空火炮威胁：在防空火炮区内，毁伤概率可表示为：

P_{G} = 1 / r

(5)

(3)地空导弹威胁：无人机在导弹区半径内被击中的可能性为：

P_{M} = \frac{R_{m a x}^{4}}{r^{4} + R_{m a x}^{4}}

(6)

其中， $R_{m a x}$ 为威胁源的最大半径.

(4)禁飞区威胁：现实中存在一些气候和环境非常恶劣的区域，称为禁飞区.禁飞区的约束为：

P_{J} = K_{J}

(7)

其中，K_J为禁飞区威胁代价.

将威胁源等效为地形模型，假设距离威胁源中心越近，威胁代价越大，地形越高，反之则越低.因此，可以将威胁源等效为：

\begin{array}{l} Δ h (x, y) = \\ \{\begin{array}{l} 0, R \geq R_{m a x, p} \\ K_{t h r} \times \sqrt[]{R_{m a x, p}^{2} - [{(x - x_{p})}^{2} + {(y - y_{p})}^{2}]} \\ e l s e \end{array} \end{array}

(8)

其中， $K_{t h r}$ 为威胁源修正系数，第p个威胁源中心的水平坐标为 $(x_{p}, y_{p})$ ，第p个威胁源的最大半径为 $R_{m a x, p}$ ，R为坐标点到威胁源中心的距离.定义每个航迹点在威胁区域的计算代价如下：

f_{T, j p} = \{\begin{array}{l} P_{0} / P_{G} / P_{M} / P_{J}, r_{j, p} \leq R_{m a x, p} \\ 0, e l s e \end{array}

(9)

其中，r_j，p 为第j个航迹点到威胁源p中心的直线距离，P₀，P_G，P_M和P_J分别为雷达、火炮、导弹、禁飞区的代价函数，f_T，jp 为航迹点j到威胁源p中心的代价.

1.3　无人机约束

无人机在飞行过程中受自身的物理约束，主要包括转弯角α、下滑及爬升角β以及燃油代价（路程）.各物理约束分别为：

J_{α_a n g l e, j} = \{\begin{matrix} \begin{matrix} 0, & α \leq α_{m a x} \end{matrix} \\ \begin{matrix} K_{α}, & α > α_{m a x} \end{matrix} \end{matrix}

(10)

J_{β_a n g l e, j} = \{\begin{matrix} \begin{matrix} 0, & β \leq β_{m a x} \end{matrix} \\ \begin{matrix} K_{β}, & β > β_{m a x} \end{matrix} \end{matrix}

(11)

J_{L, j} = \{\begin{matrix} l_{j}, j > 1 \\ 0, j = 1 \end{matrix}

(12)

其中， $K_{α}$ 和 $K_{β}$ 分别为转弯角和俯仰角威胁系数， $J_{α_a n g e l, j}$ 和 $J_{β_a n g e l, j}$ 为第j个航迹点对应α和β的代价函数， $J_{L, j}$ 为第j个航迹点对应的航程.综合各代价函数，可得出第j个航迹点的无人机自身约束代价函数为：

f_{J, j} = J_{α_a n g l e, j} + J_{β_a n g l e, j} + J_{L, j}

(13)

1.4　航迹代价函数

将地形约束、高程代价、威胁模型约束及无人机自身物理约束的代价加权综合起来就构成最终的无人机代价函数，如下所示：

F = \sum_{j = 1}^{d} (σ_{1} f_{Z, j} + σ_{2} f_{H, j} + σ_{3} \sum_{p = 1}^{w} f_{T, j p} + σ_{4} f_{J, j})

(14)

其中，F为整条航迹的代价，σ₁，σ₂，σ₃和σ₄为各代价的权重，d为航迹点的总数，w为威胁源的总数.

2 改进的SSA算法

2.1　SSA算法

麻雀是一种聪明、记忆力较好的鸟类，喜欢群居活动.SSA^［13］中的麻雀种群分为觅食发现者和抢食物的加入者，两者角色可以互换；同时，还选择了一定比例的麻雀作为侦察的警戒者，一有危险便飞向别处.整个麻雀种群的位置矩阵以及适应度表示如下：

X = [\begin{matrix} x_{11} & x_{12} & \dots & x_{1 d} \\ x_{21} & x_{22} & \dots & x_{2 d} \\ ⋮ & ⋮ & ⋱ & ⋮ \\ x_{n 1} & x_{n 2} & \dots & x_{n d} \end{matrix}]

(15)

F_{X} = [\begin{array}{l} f ([x_{11}, x_{12}, \dots, x_{1 d}]) \\ f ([x_{21}, x_{22}, \dots, x_{2 d}]) \\ ⋮ \\ f ([x_{n 1}, x_{n 2}, \dots, x_{n d}]) \end{array}]

(16)

其中，x_ij 为j维空间内第i只麻雀的位置，矩阵F_X 表示麻雀种群的适应度值.

迭代寻优过程中，麻雀种群中的发现者负责觅食和指导整个种群移动，发现者位置更新如下：

x_{i, j}^{t + 1} = \{\begin{array}{l} x_{i, j}^{t} \cdot e x p (\frac{- i}{ζ \times i t e r_{m a x}}), R_{2} < S T \\ x_{i, j}^{t} + Q \times L, R_{2} \geq S T \end{array}

(17)

其中， $x_{i, j}^{t}$ 表示种群中第t代中第i个个体的第j维位置，ζ为 $(0,1]$ 中的均匀随机数，Q为一个标准正态分布随机数，L是一行多维的全一矩阵， $R_{2}$ 为 $[0,1]$ 中的均匀随机数，ST为警戒阈值，取0.6.可以看出，当 $R_{2}$ ≥ST时，当代发现者按正态分布随机移动到父代位置附近；当 $R_{2}$ 小于ST，麻雀向原点收敛，并且随着迭代次数t的变大，步长取值范围逐渐由 $(0,1)$ 慢慢缩小为 $(0,0.4)$ ，取值范围逐渐变得均匀.加入者为除去发现者外适应度较差的一些个体，位置更新公式如下：

x_{i, j}^{t + 1} = \{\begin{array}{l} Q \cdot e x p (\frac{x_{w o r s t}^{t} - x_{i, j}^{t}}{i^{2}}), i > \frac{n}{2} \\ x_{p}^{t} + |x_{i, j}^{t} - x_{p}^{t}| \cdot A^{+} \cdot L, i \leq \frac{n}{2} \end{array}

(18)

其中， $X_{p}^{t}$ 是第t代种群发现者占据的最佳位置， $x_{w o r s t}^{t}$ 表示当前全局最差位置，A为只含1或-1元素的1×d的矩阵，定义矩阵运算 $A^{+}$ 的计算方式如下：

A^{+} = A^{T} {(A A^{T})}^{- 1}

(19)

在麻雀种群中随机选取20%的个体作为警戒者，则这些个体对全体的影响如下：

x_{i, j}^{t + 1} = \{\begin{array}{l} x_{b e s t}^{t} + δ \cdot |x_{i, j}^{t} - x_{b e s t}^{t}|, f_{i} \neq f_{g} \\ x_{i, j}^{t} + k \cdot (\frac{x_{i, j}^{t} - x_{b e s t}^{t}}{|f_{i} - f_{w}| + ε}), f_{i} = f_{g} \end{array}

(20)

其中， $x_{b e s t}^{t}$ 表示当前全局最优位置；δ是符合正态分布的步长控制参数，均值为0，方差为1；k是 $[- 1,1]$ 的随机数； $f_{i}$ 表示麻雀当前位置的适应度； $f_{g}$ 与 $f_{w}$ 分别为全局最优和最差适应度；ε为不为零的极小值，设置为 $1^{- 8}$ ，防止分母为0.

综合SSA发现者、加入者、警戒者的更新方式可知，SSA在求解原点附近解时寻优性能较好，一旦解离原点较远，性能就不如差分进化算法、遗传算法等一些经典智能算法.同时，由于SSA的收敛方式是跳跃式的，容易陷入局部最优，因此必须进一步改进.

2.2　基于改进的麻雀搜索算法的无人机三维路径规划

2.2.1　航迹编码

在航迹的仿真三维图中，路径为一条可视化的实线.本文算法中每条路径由每只麻雀代表，代价最小的麻雀代表最优路径.定义种群中的一只麻雀X_i 为一条路径， $X_{i} = [x_{i 1},$

$x_{i 2}, \dots, x_{i d}]$ ，共有d个航迹点，每个航迹点x_ij 具有空间三维的属性 $(x, y, z)$ .利用SSA规划三维的无人机突防路径时，首先确定路径总数n和航迹点数d，即麻雀种群数量n和麻雀个体维度d，然后将三维的坐标变化等效为二维的坐标变化，即将x坐标等距离固定，y和z进行迭代更新.

2.2.2　基于随机Tent映射的种群初始化

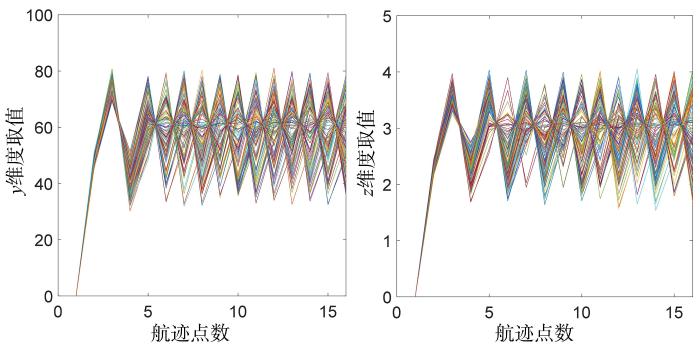
由于SSA的初始种群是随机产生的，可能会导致种群多样性不足，对迭代影响很大，采用混沌映射^［18-19］对于初始化质量有不错的效果.本文采用Tent映射来提高初始种群质量，y，z维度取值变化曲线如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 Tent混沌映射变化曲线

Fig.1 Variation curve of Tent chaotic map

现有Tent映射生成的混沌序列分布y维度集中在 $(30,80)$ ，z维度集中在 $(1.5,4)$ .因此，本文设计了一种随机Tent映射方法，公式如下：

v_{i, j + 1} = \{\begin{array}{l} ψ \times v_{i, j} + s \times c o s (v_{i, j}), v_{i, j} < 0.5 \\ ψ \times (1 - v_{i, j}) + s \times c o s (v_{i, j}), v_{i, j} \geq 0.5 \end{array}

(21)

其中，i为种群规模（ $i = 1,2, \dots, n$ ），j为个体维数（ $j = 1,2, \dots, d$ ），s为 $(0,1)$ 的随机数，ψ为混沌参数.对该式取初值后，可以得到n×d个混沌序列.将混沌序列代入个体位置公式求出种群的个体位置，公式如下：

x_{i, j} = L_{b_{j}} + v_{i, j} (U_{b_{j}} - L_{b_{j}})

(22)

其中， $U_{b_{j}}$ 和 $L_{b_{j}}$ 分别为j维搜索空间的上、下边界.如图2所示，随机Tent映射生成的混沌序列分布y维度和z维度分布更均匀.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 随机Tent混沌映射变化曲线

Fig.2 Variation curve of random Tent chaotic map

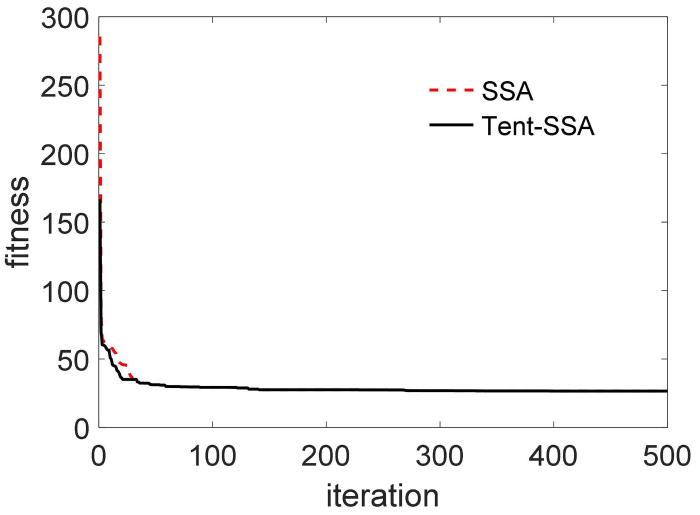
对改进初始化算法进行实验验证，使用改进Tent映射初始化种群的SSA算法并和原始SSA进行对比实验，结果如图3所示.由图可知，改进算法有效降低了初始化种群的代价，加快了迭代速度.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 代价变化曲线图

Fig.3 Cost variation curve

2.2.3　自适应领头雀引导策略

更新式（17）可知，发现者位置的更新是在父代的基础上寻优，此策略没有考虑父代的不利影响.而本文作者观察到，自然界中的麻雀群在觅食时通常由一个体型稍大、基因更优秀的个体充当领头雀.鉴于此，本文设计了一种新的自适应领头雀引导策略来完善SSA算法，使迭代更新不仅受父代的影响，还受领头雀的影响.加入领头雀引导在前期会不利于种群全局探索能力的提升，所以，为了同时增加算法的前期全局探索和后期局部寻优的能力，在上述最优个体（领头雀）引导策略的基础上再添加自适应权重，这里新的发现者的更新公式修订为：

\begin{array}{l} x_{i}^{t + 1} = \\ \{\begin{array}{l} \frac{1}{2} \times [(ω \cdot x_{i}^{t} + (1 - ω) \cdot x_{1}^{t}) \cdot e x p (\frac{- i}{α \times i t e r_{m a x}}), \\ R_{2} < S T \\ x_{i}^{t} + Q \times L, R_{2} \geq S T \end{array} \end{array}

(23)

其中， $x_{1}^{t}$ 表示种群中第t代中最优个体，ω为权重因子.更新公式如下：

ω (t) = ω_{m a x} - (ω_{m a x} - ω_{m i n}) \times \frac{2}{π} \times a r c s i n \frac{t}{T_{m a x}}

(24)

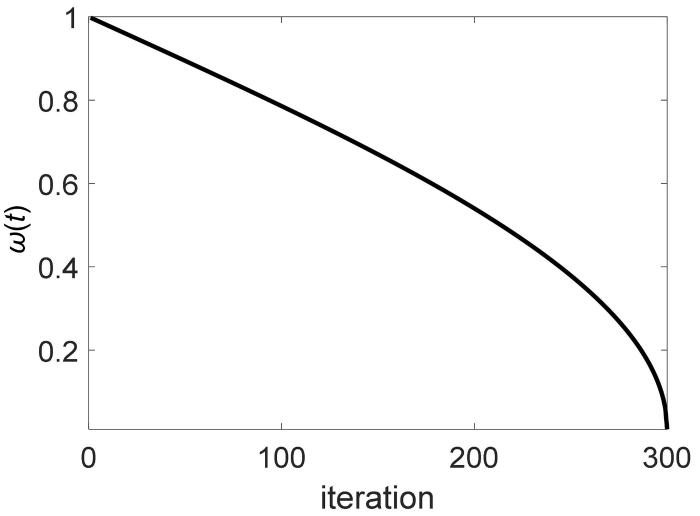
其中， $ω_{m a x}, ω_{m i n}$ 分别为最大值和最小值.针对种群个体y维度更新 $ω$ ， $ω_{m a x} 和 ω_{m i n}$ 取1和0.01，z维度的更新取0.1和0.005.y维度的ω系数变化曲线如图4所示，z维度变化趋势相似，不再放图.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 ω系数变化曲线图

Fig.4 Variation curves of ω

迭代前期快速减小的权重可能会导致陷入局部最优.本文中ω的改变在前中期减小较为缓慢，使得发现者的更新受父代的影响较大，降低算法早熟的可能性；后期的减小很迅速，受领头雀的影响较大，提高了算法的精度，使寻找到的路径适应度更好.

对自适应领头雀引导策略进行实验验证，发现者更新公式采用式（23），并和原始SSA进行对比实验，结果如图5所示.可知，改进算法可以有效加快迭代速度.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 自适应领头雀引导策略与原始SSA收敛曲线对比

Fig.5 Convergence curves of Adaptive Leading Sparrow Guide strategy and original SSA

2.2.4　中心变异⁃进化因子的设计

SSA在迭代过程中容易陷入局部最优，导致寻优路径停滞不变，所以，本文提出一种基于个体中心的变异方法，效果如图6所示.红色虚线为初始路径点连成的线，利用初始点计算其中心位置；黑色实线中的每个点由初始点与中心点的连线上随机取一个点得来，将每个点连接起来就又是一条路径.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 中心变异效果图

Fig.6 Central variation effect diagram

为加快迭代速度，只选取最优个体进行中心变异，设 $X_{m} = [x_{1}, x_{2}, \dots, x_{d}]$ 是带有单位质量的d个点，则一个离散均匀的整体中心G为：

G = \frac{x_{1} + x_{2} + \dots + x_{d}}{d}

(25)

则该整体中某一点x_j 的中心变异点定义为：

g_{1} (x) = {\bar{x}}_{j} = r a n d (x_{j}, G), j = 1,2, \dots, d

(26)

采用弱肉强食的原则来设计进化部分，通过适应度值的好坏来对种群进行排序，按照顺序进化.可以看出，适应度好的个体有大概率保留下来，较差的个体大概率选择进化，公式如下：

g_{2} (x) = x_{i}^{} = \{\begin{matrix} x_{i}^{}, s < P (i) \\ x_{1} - r a n d \cdot (x_{t_{1}} - x_{t_{2}}), e l s e \end{matrix}

(27)

其中， $t_{1}, t_{2}$ 为种群n个个体中的随机个体，且互不相同； $x_{1}$ 为最优个体；rand和s为0~1的随机数； $P (i)$ 为种群中第i个个体对应的适应度级别，计算公式为：

P (i) = \frac{n - i + 1}{n}

(28)

中心变异与进化过程都可以增加种群的多样性，扩大搜索范围.中心变异产生的解相对固定，而进化的解随机性大.本文融合了这两种策略：在算法前期，大概率选择中心变异；在算法后期，种群趋于稳定，此时较大概率采用进化，可以增大种群的随机性.通过中心变异⁃进化因子产生新解的计算公式可以表示为：

x_{i}^{n e w} = \{\begin{array}{l} g_{1} (x), s < τ \\ g_{2} (x), e l s e \end{array}

(29)

其中， $g_{1} (x)$ 为中心变异； $g_{2} (x)$ 为进化； $τ$ 为选择中心变异或进化的概率，计算公式如下：

τ = 1 - \frac{t}{T_{m a x}}

(30)

采用中心变异⁃进化因子求取新解之后，根据贪婪原则更新得到的新种群.

对中心变异⁃进化因子增加种群多样性进行实验验证，并和原始SSA进行对比实验，实验结果如图7所示.由图可知，改进算法可以有效地加强全局勘探能力.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 中心变异⁃进化因子策略和原始SSA收敛曲线对比

Fig.7 Convergence curves of center Mutation⁃evolution Factor strategy and orginial SSA

2.2.5　三次样条插值平滑路径

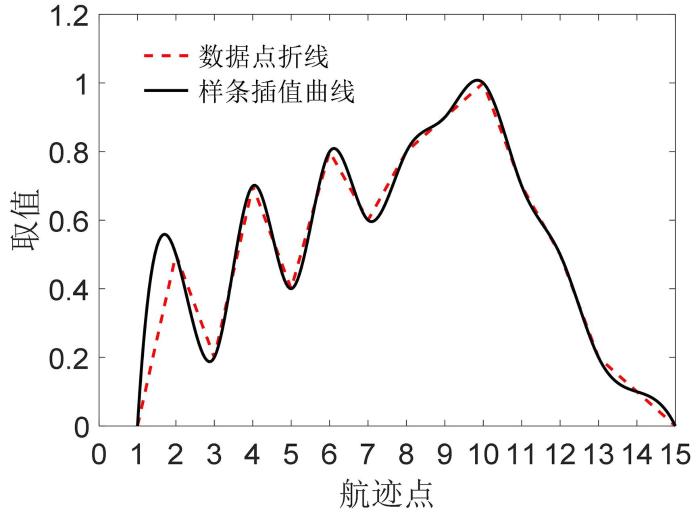
在无人机实际飞行中，通过算法寻优获得路径点，采用三次样条平滑路径.设最终无人机突防路径为L=（l₁，l₂，…，l_d ），做三次样条插值，最终形成一条光滑路径，三次样条插值效果如图8所示.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 三次样条插值优化效果图

Fig.8 Optimization results of cubic spline interpolation

算法的具体流程如下所示.

步骤1.随机Tent映射初始化种群

确定地形及威胁环境，确定航迹点数目d与种群数目n，根据式(21)与式(22)随机Tent映射初始化种群，计算种群的适应度并排序，选出最优个体与最差个体.

步骤2.种群减少

SSA在路径搜索上迭代速度较慢，借鉴麻雀种群秋冬季的种群大小不同，算法前期（秋季）使用大种群，后期（冬季）变为小种群，即种群大小变为原来的1/2.

步骤3.迭代更新

选取适应度高的前PD只个体作为发现者，根据自适应领头雀引导策略，即式(23)和式(24)来更新发现者；余下个体作为跟随者，根据式(18)和式(19)更新坐标位置；从种群中随机选取SD只个体作为警戒者，根据式(20)更新坐标位置.

步骤4.边界限定

根据三维空间的大小限定航迹点的范围，若航迹点某一维超出边界，则用航迹点此维的边界值代替.

步骤5.中心变异⁃进化因子计算新种群

通过比较随机数与选择中心变异还是进化的概率的大小来选择对于种群是进行中心变异还是进化.中心变异是基于原最优个体的中心点来随机变异出一个新的个体，进化的原则是对于适应度好的大概率保留，适应度差的大概率淘汰.根据式（25）至式（30）来计算中心变异⁃进化后的种群，然后根据贪婪原则选择是否代替原种群.

步骤6.判断终止条件

判断是否达到迭代次数，未达到则跳回步骤2，达到则结束，输出最终的路径点并进行三次样条插值平滑路径.

算法的流程图如图9所示.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 本文算法流程图

Fig.9 Flow chart of this algorithm

3 算法测试

为了验证改进算法的性能，将本文算法与SSA^［13］，GWO^［7］，MFO^［8］进行比较，测试函数如

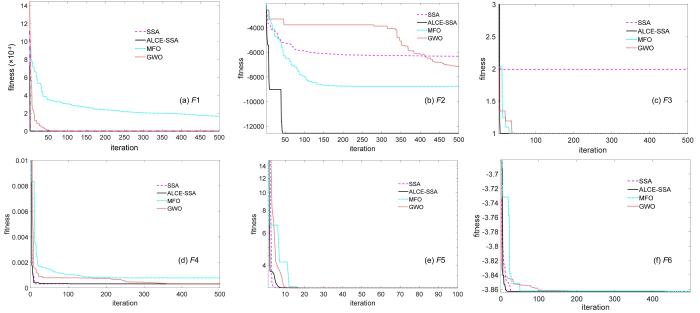
表1所示.每个算法对各个测试函数运行30次，得到测试的平均值与标准差，如表2所示.测试函数的收敛曲线如图10所示.设置种群的规模为50，迭代次数为500.

表1 测试函数

Table 1 Test functions

ID	函数	维度	定义域	极小值	类型
F1	$f (x) = \sum_{i = 1}^{n} {(\sum_{j = 1}^{i} x_{j})}^{2}$	30	$[- 100,100]$	0	单峰
F2	$f (x) = \sum_{i = 1}^{n} - x_{i} s i n (\sqrt[]{\|x_{i}\|})$	30	$[- 500,500]$	$- 418.98 \times 30$	多峰
F3	$f (x) = {[\frac{1}{500} + \sum_{j = 1}^{25} \frac{1}{j + \sum_{i = 1}^{2} {(x_{i} - a_{i j})}^{6}}]}^{- 1}$	2	$[- 65,65]$	1	多峰
F4	$f (x) = {\sum_{i - 1}^{11} [a_{i} - \frac{x_{1} (b_{i}^{2} + b_{1} x_{2})}{b_{i}^{2} + b_{1} x_{3} + x_{4}}]}^{2}$	2	$[- 5,5]$	0.0003	多峰
F5	$\begin{array}{l} f (x) = [1 + {(x_{1} + x_{2} + 1)}^{2} \times (19 - 14 x_{1} + 3 x_{1}^{2} - 14 x_{2} + 6 x_{1} x_{2} + 3 x_{2}^{2})] \times \\ [30 + {(2 x_{1} - 3 x_{2})}^{2} \times (18 - 32 x_{1} + 12 x_{1}^{2} - 48 x_{2} - 36 x_{1} x_{2} + 27 x_{2}^{2})] \end{array}$	2	$[- 2,2]$	3	多峰
F6	$f (x) = - \sum_{i = 1}^{4} c_{i} e x p [- \sum_{j = 1}^{3} a_{i j} {(x_{j} - p_{i j})}^{2}]$	3	$[1,3]$	$- 3$	多峰

新窗口打开| 下载CSV

表2 本文算法和对比算法在六个测试函数上的测试结果比较

Table 2 Test results of our algorithm and toher algorithms on six test functions

ID	本文算法		SSA		MFO		GWO
ID	Mean	Std	Mean	Std	Mean	Std	Mean	Std
F1	0.00E+00	0.00E+00	0.00E+00	0.00E+00	3.27E+04	3.86E-07	6.11E-10	2.45E-05
F2	-1.26E+04	7.16E-08	-6.32E+03	6.82E-07	-8.68E+03	4.25E-07	-5.34E+03	3.57E-05
F3	1.00E+00	7.21E-10	1.94E+00	3.09E-11	1.00E+00	9.03E-09	1.00E+00	5.69E-12
F4	3.20E-04	2.81E-08	3.08E-04	7.86E-15	3.08E-04	3.45E-05	7.83E-04	2.05E-07
F5	3.00E+00	0.00E+00	3.00E+00	0.00E+00	3.00E+00	0.00E+00	3.00E+00	0.00E+00
F6	-3.86E+00	8.21E-10	-3.86E+00	7.58E-05	-3.86E+00	7.25E-09	-3.86E+00	5.95E-06

新窗口打开| 下载CSV

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 本文算法和对比算法在六个测试函数上的收敛曲线

Fig.10 Function convergence curve of our algorithm and other algorithms on six test functions

表2的平均值、标准差和图10的函数收敛曲线表明，本文算法在求解各函数时都表现出优异性能.对于函数F1，ALCE⁃SSA算法优于GWO和MFO；对于函数F2和F6，ALCE⁃SSA算法优于GWO，MFO和SSA；对于函数F3，ALCE⁃SSA算法优于GWO，MFO和SSA；对于函数F4和F5，ALCE⁃SSA算法次于SSA，但优于GWO和MFO.上述函数中F2是一种较复杂的测试函数，大部分优化算法无法找到最优值，SSA，GWO，MFO三种算法对于求解F2的结果与实际最优解的误差极大，而本文算法在迭代50次左右找到最优值，证明本文算法在求解复杂函数时的优越性.通过六种函数测试对比了本文算法与其他三种算法的性能，证明提出的算法可以很好地改善SSA算法全局寻优的能力，表现较优.

4 无人机突防仿真计算与分析

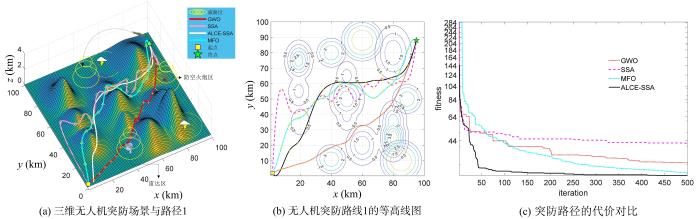
仿真平台的硬件是Intel Core i5⁃7300 HQ CPU 2.60 GHz、内存8 GB的计算机，编译软件为Matlab R2017b.两个测试地形区域为100 km×100 km，测试限高5 km，建立双模型增加算法的可信度.模型1如图11a所示，我方无人机航线起点与敌方目标点分别为 $(2,2, 0.2)$ 及 $(99,88,0.5)$ ，敌方雷达及火炮距离的中心为 $(40,80,0) (89,50,0)$

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 模型1仿真结果图

Fig.11 Simulation results of Model 1

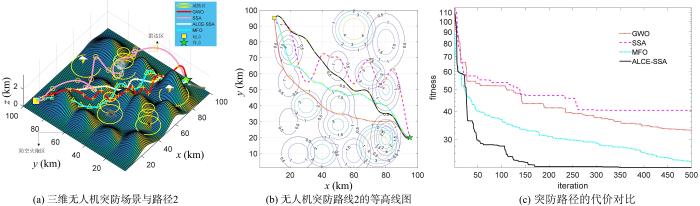
$(40,11,0)$ ，威胁区最大作用半径为11 km；禁飞区中心为 $(85,10,0) (60,88,0)$ ，作用半径为15 km.仿真结果如图11c所示.模型2如图12a所示，起点与目标点分别为 $(10,95,0.2) (95,20,0.5)$ ，敌方雷达及火炮距离的中心为 $(30,40,0) (70,60,0)$ $(40,11,0)$ ，禁飞区中心为 $(75,15,0) (60,88,0)$ ，仿真结果如图12c所示.各算法种群数设为100，最大迭代次数500次.算法参数如表3所示.

图12

新窗口打开| 下载原图ZIP| 生成PPT

图12 模型2仿真结果图

Fig.12 Simulation results of Model 2

表3 算法的相关参数

Table 3 Relevant parameters of the algorithm

参数	符号	参数值
地形威胁系数	$K_{Z}$	100
地形威胁系数	$K_{Z}^{'}$	10
禁飞区威胁系数	$K_{J}$	100
转弯角最大角度	$α_{m a x}$	60°
俯仰角最大角度	$β_{m a x}$	60°
俯仰角威胁系数	$K_{β}$	10
威胁源修正系数	K_thr	$1 / 3 \times R_{m a x, p}$
地形约束权值	$σ_{1}$	0.25
高程约束权值	$σ_{2}$	0.4
威胁源约束权值	$σ_{3}$	0.2
物理约束权值	$σ_{4}$	0.15
航迹点数	d	15
种群数量	n	100

新窗口打开| 下载CSV

图11a由山脉、威胁源（黄色区域）、路径组成.通过本文算法ALCE⁃SSA与SSA^［13］，GWO^［7］和MFO^［8］在无人机突防路线轨迹图中的对比可以看出，GWO的规划路线（红线）普遍飞行高度高，没有避开威胁源；GWO的后期寻优能力差，导致路径点的某些维度误差较大；MFO（蓝线）中飞蛾更新机制使得全局寻优能力较强，三维路径图中的路径规划确实躲开了威胁源，找到了一条相对较优的路径，但是路径总体不够平滑，飞行难度大；SSA（粉线）规划的路径中飞行高度上下起伏，路径不够平滑；本文ALCE⁃SSA算法（白线）可以有效地避开威胁源，近似于沿着地图对角线生成一条较优的路径，较平滑，飞行难度降低，并且能实现低空飞行，完成低空突防目标.

从图11b无人机突防场景与路径的等高线图可以看出，GWO，MFO，ALCE⁃SSA在规划路径转弯角方面较平滑，SSA规划的路径较曲折.

图11c为突防路径的代价曲线，可见SSA的收敛速度比GWO，MFO的更新更快，但迭代30次左右便陷入局部最优；GWO在复杂度较高时收敛较慢，后期局部寻优能力差导致精度较差，代价收敛于35左右；MFO算法在路径搜索方面的全局寻优能力优秀，但搜索速度较慢，迭代500次左右寻找到一条较优的路径；本文算法兼具迭代速度快和全局寻优强的优点，迭代50次左右就可以寻找到一条较优路径，之后开始局部寻优，最终找到一条代价为25左右的路径.证明ALCE⁃SSA在无人机路径规划方面的效果更好.

图12为模型2的仿真结果，验证模型1的结论.由图可见，模型1的SSA算法更新速度快但易陷入局部最优，GWO算法的后期寻优能力差导致某些路径点维度的精度差，MFO算法的全局寻优能力强但更新速度慢.由于路径规划不存在绝对最优解，但存在相对最优解，四种算法的轨迹相比，ALCE⁃SSA是符合条件的相对最优解.

搜索路径50次后对航程、转弯及俯仰角代价、最优代价取平均值，并统计搜索路径的成功率（判断路径是否穿过山脉和威胁区，成功率是50次实验中算法搜索路径成功的次数除以50）以及收敛时间.根据图11c和图12c的迭代曲线选择合适的收敛时间作为收敛代价.统计图11中GWO迭代次数为400次的收敛时间；同理，MFO为500次，SSA为150次，ALCE⁃SSA为100次.图12中GWO为500次，MFO为500次，SSA为250次，ALCE⁃SSA为175次.如表4和表5所示.

表4 本文算法和对比算法在模型1上的实验结果

Table 4 Experimental results of Model 1 by our algorithm and other algorithms

算法	航程 (km)	转弯及俯仰角代价	最优代价	时间代价 (s)	寻优成功率
ALCE⁃SSA	135.87	0	24.62	25.68	98%
GWO	145.95	60	34.35	96.32	82%
MFO	147.95	30	25.53	120.47	90%
SSA	181.84	160	42.61	60.14	62%

新窗口打开| 下载CSV

表5 本文算法和对比算法在模型2上的实验结果

Table 5 Experimental results of Model 2 by our algorithm and other algorithms

算法	航程 (km)	转弯及俯仰角代价	最优代价	时间代价 (s)	寻优成功率
ALCE⁃SSA	130.35	0	22.51	43.56	100%
GWO	166.78	120	32.56	128.12	86%
MFO	147.51	60	24.95	122.44	92%
SSA	197.63	180	40.36	100.36	70%

新窗口打开| 下载CSV

根据表4的数据，ALCE⁃SSA规划的路径比SSA，MFO及GWO算法分别减短45.98，12.09和10.08 km，最优代价比其他三种算法分别降低17.99，0.91和9.91，时间代价比SSA，MFO及GWO减少34.46，94.79和70.64 s，并拥有98%的成功率.

根据表5的数据，ALCE⁃SSA规划的路径比SSA，MFO及GWO算法分别减短67.28，17.16和36.43 km，最优代价比其他三种算法分别降低17.85，2.44和10.05，时间代价比SSA，MFO及GWO降低56.8，78.88和84.56 s，并拥有100%的成功率.

以上结果证明，ALCE⁃SSA算法的航程、转弯及俯仰角代价、最优代价、寻优成功率、时间代价等评价指标均优于其他三种算法.

对图11模型搜索路径50次后航迹点的飞行高度取平均值，绘制各算法航迹的航程⁃高度图，如图13所示.

图13

新窗口打开| 下载原图ZIP| 生成PPT

图13 飞行高度(a)和飞行高度与地形高度差(b)

Fig.13 Flight path altitude (a) and altitude difference (b)

一共选取16个航迹点，经三次样条插值后形成一条低空突防的路径.图13显示了各个算法规划路径的各个航迹点的高度对比曲线，本文算法的高度曲线最低，然后是MFO，GWO，最后是SSA.从图中高度的变化也可看出，本文算法的爬升以及下滑角度的代价最小，GWO和SSA算法在各个航迹点的高度之间有巨大变化，对于无人机的性能有较大的要求.图13b显示了各个航迹点的飞行高度与地形的高度差，主要体现低空突防的性能.可以看出，GWO和SSA的飞行高度差较大，变化较快，表现较差，而本文算法与MFO算法的高度差都有较好的表现.为进一步比较性能，求和各航迹点的高度与高度差，如表6所示.

表6 航迹点高度和与高度差和 (km)

Table 6 Sum of track point altitude and altitude difference

算法	GWO	SSA	MFO	ALCE⁃SSA
航迹点高度和	2.28E+01	2.66E+01	1.21E+01	5.46E+00
航迹点高度差和	9.69E+00	1.94E+01	5.43E+00	4.67E+00

新窗口打开| 下载CSV

统计求和各航迹点的高度与高度差，对于高度和，ALCE⁃SSA规划路径的总高度和比SSA，MFO及GWO降低了21.14，6.64和17.34 km；高度差的和，ALCE⁃SSA规划路径时比SSA，MFO及GWO降低14.73，0.76和5.02 km.本文算法的高度差的和优于MFO，证明本文算法在低空突防的路径规划上有更优的表现.

5 结论

本文提出一种基于改进SSA算法来解决三维无人机低空突防问题.首先建立地形和威胁源模型，根据模型确定威胁代价；设计随机Tent映射初始化种群，提高初始化种群的质量；在发现者位置更新上采用自适应领头雀引导策略，解决鸟群发现者在更新位置上父代带来的不利影响；采用中心变异⁃进化因子提高种群多样性，防止种群陷入局部最优，提高全局搜索能力；采用最优个体样条插值随机取点法，使路径点均匀分布在地图上，解决路径点过于密集的问题.实验结果表明，ALCE⁃SSA可以更精确、快速地使无人机自主避开危险区域选择最优路径，实现低空突防.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Zhang

， Wu

， Dai

J Y

，et al.

A novel real⁃time penetration path planning algorithm for stealth UAV in 3D complex dynamic environment

IEEE Access，2020(8)：122757-122771.