基于反卷积算法的超声图像优化方法

doi:10.13232/j.cnki.jnju.2023.02.007

基于反卷积算法的超声图像优化方法

王岳宁¹, 郭成雯¹, 王育昕¹, 袁杰^,¹, 程茜²

1.南京大学电子科学与工程学院，南京，210023

2.同济大学物理科学与工程学院，上海，200092

Ultrasound image optimization method based on deconvolution algorithm

Wang Yuening¹, Guo Chengwen¹, Wang Yuxin¹, Yuan Jie^,¹, Cheng Qian²

1.School of Electronic Science and Engineering, Nanjing University, Nanjing, 210023, China

2.School of Physics Science and Engineering, Tongji University, Shanghai, 200092, China

通讯作者: E⁃mail：yuanjie@nju.edu.cn

收稿日期: 2022-11-02

基金资助:

科技部重点研发计划项目. 2017YFC0111402

Received: 2022-11-02

摘要

超声成像技术因其无侵入、低成本、快速、可便携化的特性，成为医学成像领域的一大研究热点.然而，受限于声波的传播特性、成像算法的弊端以及硬件发展，超声图像存在成像深度小、大量伪影、分辨率低等问题.针对超声图像中的目标混叠和分辨率低下问题，提出了一种基于信号处理的超声图像优化方法，通过反卷积算法对超声探头采集到的原始信号进行处理，再将处理后的信号按照延时求和成像算法重建为图像.提出的方法可以减轻信号间的混叠，最终减轻图像中的混叠，令图像中原本难以辨认的微小结构和细节信息得以展现.通过仿真和实验证明，经过处理后的信号所重建的图像质量优于原始信号所重建的图像，验证了提出的信号处理方法的有效性.

关键词： 超声图像 ; 图像优化 ; 信号处理 ; 反卷积

Abstract

Ultrasound imaging has become a research hotspot in the field of medical imaging due to its non⁃invasive,low⁃cost,rapid and portable characteristics. However,limited by the propagation characteristics of sound waves,the shortcomings of imaging algorithms and the development of hardware,ultrasound imaging has some problems such as small imaging depth,a large number of artifacts and low resolution. In order to solve the problems of target aliasing and low resolution in ultrasound image,this paper proposes an ultrasound image optimization method which processes the original signals detected by the ultrasonic probe based on the deconvolution algorithm. The method proposed in this paper can reduce the signal alising,and finally reduce the aliasing in the ultrasound image,so that the originally unrecognizable tiny structure and detailed information in the image can be seen. Carried out simulations and experiments for ultrasound imaging,the ultrasound image quality reconstructed by the processed signal is better than that reconstructed by the original signal which verifies the validity of the ultrasound image optimization method proposed here.

Keywords： ultrasound image ; image optimization ; signal processing ; deconvolution

PDF (1074KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王岳宁, 郭成雯, 王育昕, 袁杰, 程茜. 基于反卷积算法的超声图像优化方法. 南京大学学报（自然科学）[J], 2023, 59(2): 247-255 doi:10.13232/j.cnki.jnju.2023.02.007

Wang Yuening, Guo Chengwen, Wang Yuxin, Yuan Jie, Cheng Qian. Ultrasound image optimization method based on deconvolution algorithm. Journal of nanjing University[J], 2023, 59(2): 247-255 doi:10.13232/j.cnki.jnju.2023.02.007

超声重建算法的瓶颈分为两个部分：一是由于声波本身的衍射特性，导致图像中的分辨率受限；二是由于伪影的存在，导致图像信噪比低、模糊、边界不清晰.分辨率受限的问题，是由于声波在介质中传播时会发生衍射，导致图像的分辨率受到瑞利准则的限制.瑞利准则指的是当成像区域中某两个目标之间的距离小于一个确定的阈值时，这两个目标是无法被区分的.阈值与传感器采样频率和声波的波长有关.伪影的问题，则是因为在重建算法延时叠加的时候，非目标区域也会被叠加出一定的幅值，尤其是目标的周围伪影相对更大，所以在图中会呈现出灰色.当目标点相邻很近时，伪影也会在周围出现，呈亮度较高的灰色，从视觉上误将目标点与伪影都看作为目标，进而导致超声图像中模糊、边界不清晰、信噪比低.基于这两个问题，在成像目标距离很近时，图像中会出现目标混叠的问题.

在优化超声图像质量的研究中，利用反卷积算法对超声信号进行处理，减轻信号之间的混叠，减少图像中邻近目标的混叠是研究热点.Jensen et al^［1］于1993年提出了一种基于反卷积的超声重建算法，该算法可以将轴向分辨率提升2.4倍.Michailovich et al^［2］在2007年提出了一种对超声图像进行盲反卷积的方法，用于提升图像分辨率.Morin et al^［3］在2013年提出了一种新颖的基于半盲反卷积和交替方向法的算法，用于对超声图像进行复原，并证明了半盲反卷积相对于常规反卷积方法来说有更好的鲁棒性.Kruger et al^［4］和Gamelin et al^［5］分别在2003年和2009年在研究中将反卷积算法应用于光声图像的重建算法中，获得更好的成像效果.Cai et al^［6］在2016年提出了基于反卷积算法直接应用于三维的光声显微图像，用于提升显微图像的横向与轴向分辨率.孔垂硕等人^［7］于2018年利用盲反卷积信号复原算法重建超声合成孔径信号，提高了超声合成孔径图像分辨率.Hourani et al^［8］于2020年通过最小化损失函数对基波和谐波图像进行联合反卷积，结合了谐波信号的良好空间分辨率和基波信号的良好信噪比.Aetesam et al^［9］于2020年通过构建变分框架对从超声传感器获得的超声图像进行反卷积，优化了超声图像质量.

反卷积算法应用于超声成像时的主要目的是为了提升图像分辨率，本文所提出基于原始信号处理的反卷积超声图像优化方法并不仅仅是单纯提升分辨率，而是减轻图像临近目标之间的混叠，是一种针对原始采集信号的信号处理方法，进而提高超声图像质量.

1 相关理论

1.1　超声图像重建算法

重建算法是将超声传感器采集到的多维信号转变为图像的理论依据.声压信号是通过放置在声源表面的超声传感器采集得到的.在仅仅拥有多维度信号而组织内部的声源情况未知的前提下，重建内部的声源分布，相当于求解一个逆问题，即根据声信号获得声源.延时叠加算法^［10］（反投影算法）是目前最通用、经典的重建算法.

延时叠加算法是一种基于延时求和的合成聚焦方法.将阵元所采集到的信号进行时延再叠加，以补偿从该位置到传感器单元所在位置所需要的不同的声波传输时间.对阵元所采集的信号按照相应的时延进行加窗，窗的宽度等于通过该阵元的声传输时间.然后对加窗后的信号进行求和，根据叠加出的成像空间的幅值的分布来辨认成像空间的源分布.以单个阵元来看，假设介质均匀、声速是固定的，当距离相同时，时延就相同，所以单个阵元采集到的信号会叠加在以阵元为圆心的圆弧上，这就导致了伪影的产生.

1.2　反卷积算法

反卷积算法^［11］是一种常见的信号处理算法，从数学上说，单个特征波形与不同延时的激励信号的卷积结果是多个延时不同的特征波形的线性叠加，每个波的具体大小取决于对应位置的激励信号的幅值大小.超声成像的信号是由超声传感器采集得到，可将这个信号看作一系列脉冲信号与单个特征信号的卷积结果.这个特征信号的形状由这种成像方式本身和采集设备共同决定.所以在此假设下，可以通过反卷积运算得到一系列的正脉冲信号，而这些反卷积得到的正脉冲信号由于包含了振幅和时间信息，在延时叠加的重建算法中是可以替代原始信号来进行图像重建的.

一般地，采集到的信号可以按照公式（1）进行表示：

s (n) = o (n) * h (n) + n (n)

(1)

其中， $*$ 表示卷积运算， $h (n)$ 是这个信号卷积系统中的卷积核，这个概念类似于图像反卷积中的点扩散函数（PSF）， $s (n)$ 为超声探头采集到的原始信号， $o (n)$ 是我们想要获得的反卷积后的信号， $n (n)$ 代表加性噪声.在已知 $s (n)$ ， $h (n)$ 和信噪比时，利用 $h (n)$ 为反卷积核来进行反卷积，获得 $o (n)$ .

关于反卷积核 $h (n)$ ，不同的成像方式具有完全不同形状的反卷积核，可将其视为这种成像方式中的特征信号（用该成像方式采集质点时的信号）.在超声成像中，通常会将理想声波反射质点的超声信号（即超声的特征信号）视为一个与W形状类似的双极信号^［12-13］.不同的采集设备也会对反卷积核造成频率和幅值上的影响.

在本文中，反卷积核是通过实测的方式获取.以一个质点为采集目标时，所采集到的信号即为适用于该采集系统的反卷积核.同时，由于瑞利效应的影响，每个采集系统可采集目标的尺寸是有限制的，所以我们将该系统所能采集到的最小尺寸目标视为质点.以此类推，以系统所能采集的最小尺寸目标为成像目标，接收到的信号就是适用于该系统的反卷积核.计算最小尺寸的公式（2）为：

d = \frac{V}{f}

(2)

其中， $d$ 为该超声探头能采集到的最小尺寸， $V$ 为介质中的声波传输速度， $f$ 为超声探头的中心频率.

维纳滤波是一种常用的反卷积算法.对于超声信号这种低信噪比的信号来说，它能将噪声在反卷积中的影响最小化，使反卷积的结果更加精确.基于式（1），维纳反卷积的原理就是获得 $g (n)$ ， $g (n)$ 是 $o (n)$ 的一个估计，它们之间的均方误差最小.维纳反卷积会将计算映射到频域中，在频域中（公式（3）），

G (f) = \frac{H^{*} (f) S_{f} (f)}{{|H (f)|}^{2} S_{f} (f) + S_{η} (f)} S (f)

(3)

其中， $G (f)$ 是 $g (n)$ 的频域形式， $H (f)$ 是 $h (n)$ 的频域形式， $S (f)$ 是 $s (n)$ 的频域形式， $S_{f} (f)$ 是目标信号 $o (n)$ 的平均功率谱密度， $S_{η} (f)$ 是 $n (n)$ 的功率谱密度， $*$ 表示共轭运算.式（3）可以被重写为公式（4）：

G (f) = \frac{1}{H (f)} [\frac{{|H (f)|}^{2}}{{|H (f)|}^{2} + \frac{1}{S N R (f)}}] S (f)

(4)

其中， $S N R (f) = \frac{S_{f} (f)}{S_{η} (f)}$ 是信噪比，在这里使用原始采集信号的信噪比.所以， $\frac{1}{S N R (f)}$ 即为信号的噪信比.

本文的仿真部分使用的是无噪信号，噪信比为0.为了估计实验部分中信号的信噪比，先选择一帧信号，并给出一个信噪比的初始值（例如10 dB），然后对按照这个信噪比值进行反卷积后的信号进行图像重建.根据重建结果，不断调整信噪比的值，直到图像达到最优质量.这个信噪比可以视为最接近真实的信噪比，将其记录下来，以便在以后的反卷积过程中用于其他情况.

维纳反卷积的仿真效果如图1所示，图1a是反卷积核，图1b是原始信号与反卷积后的信号的对比，蓝色信号是原始信号，红色信号是反卷积后的信号，从图中可以看到，反卷积后的信号由双极信号变成了单极信号，且信号的宽度变窄.图中反卷积后的信号有一些滞后是反卷积导致的，滞后多少则由反卷积核的长度决定，为了与原始信号对齐，在成像前会对信号在横轴上进行平移.

图1

新窗口打开| 下载原图ZIP| 生成PPT

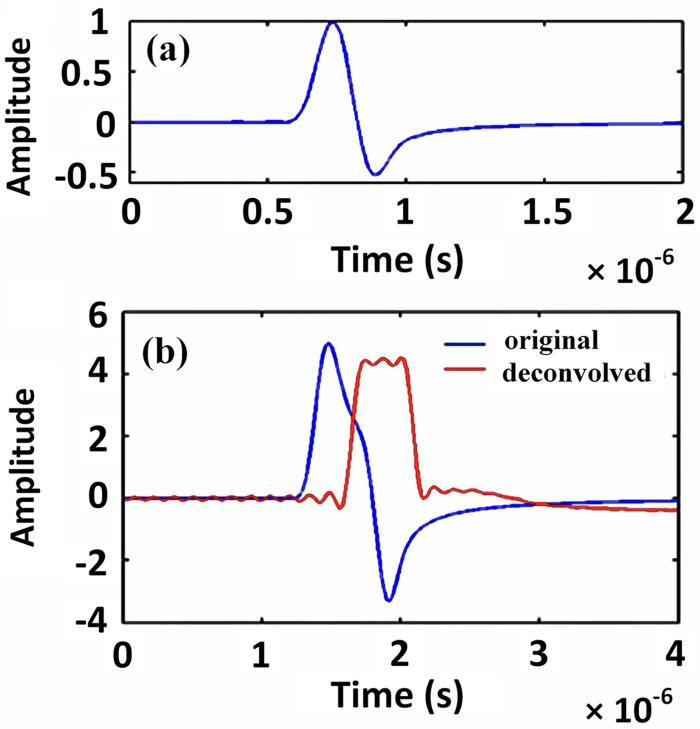
图1 (a)反卷积核;(b)原始信号与反卷积后的信号的对比

Fig.1 (a) The deconvolution kernel, (b) the contrast between the original signal and the signal after deconvolution

1.3　图像熵

在图像中，图像熵表示图像信源的平均信息量，是一种对灰度图像灰度值分布的统计度量指标，可以用来表征图像中灰度分布的聚集特征.图像熵的计算方式见公式（5）：

E n t r o p y = - \sum p_{i} * l o g (p_{i})

(5)

其中， $p_{i}$ 是某个灰度在该图像中出现的概率.在超声图像评价中，图像的灰度分布越均匀，灰度分布在分散的灰度值上，图像表现为混叠程度高，图像的熵变大；图像的灰度分布越密集，灰度分布在集中的灰度值上，图像表现为混叠程度低，图像的熵变小.混叠和伪影会导致图像中灰度更加丰富，灰度分布更均匀，使得图像熵增大^［14-17］，图像熵可作为超声图像抗混叠程度优劣的比较参量.

2 实验与结果

2.1　仿真实验

仿真实验采用基于MATLAB的第三方工具箱k⁃Wave toolbox^［18-19］进行超声仿真.使用k⁃Wave对成像目标建模，预先设置传感器发射的声波特征波形，仿真声波信号传输与反射过程，然后获取传感器采集的原始信号.超声仿真环境是运行在服务器上的64位MATLAB R2013b上的k⁃Wave工具箱，服务器的配置为双核Intel （R） Xeon （R） X5670 的CPU和72.0 GB 的RAM.超声波由放置于成像区域上方的线性128阵元超声传感器发射，然后由同一个传感器进行接收.超声波的发射方式为平面波，即所有阵元同时发射相同形状相同幅值的声波.介质中的声速设定为1540 m·s^-1.

在超声仿真中，反卷积核有两种方法来获取：一是通过在成像区域设置单个直径为1（以仿真的最小网格尺寸为单位）的反射特性近似完美的点作为目标，通过位于成像区域上方的单个传感器阵元来接收该质点的信号，该信号即为该仿真系统的反卷积核；第二个方式就是采用自定义的声源信号作为反卷积核，因为这是该系统中声波的特征信号.在本文中，两种方式都有尝试，且通过这两种方式得到的反卷积核是一样的.

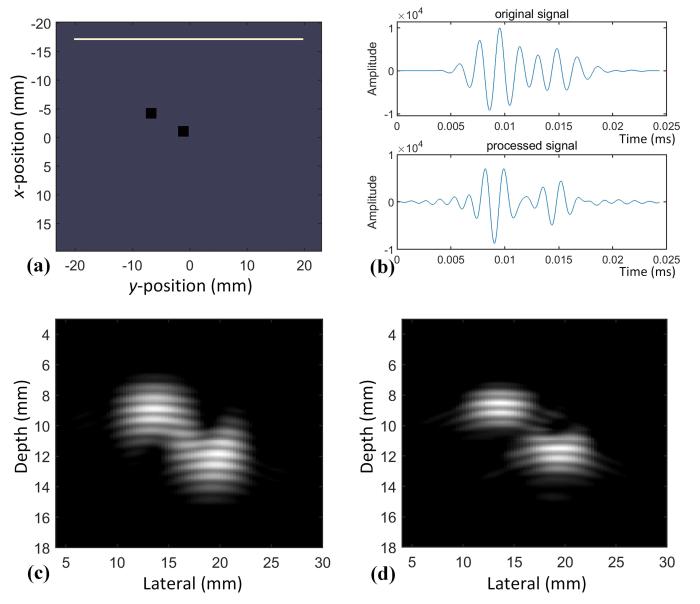
图2是本文反卷积方法应用于超声仿真模型时的信号处理和图像重建结果展示.图2a是本仿真中使用的数值模型的示意图.位于图像上方的一条横线代表传感器的摆放位置，整体背景为灰色是因为我们将整个成像区域（介质）的密度设置为1000 kg·m^-3（即为水的密度），位于介质中间的两个点的密度被设置为10000 kg·m^-3，是本次仿真中的成像目标.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 超声仿真模型的信号处理和图像重建结果对比：(a)成像目标与传感器的位置设定；(b)信号处理过程；

(c)原始信号重建出的图像；(d)反卷积后的信号重建出的图像

Fig.2 The comparison of signal processing and image reconstruction in ultrasonic simulation：(a) the position setting of the imaging target and the sensor，(b) the signal processing process，(c) the image reconstructed from the original signal，(d) the image reconstructed from the deconvolution signal

从图2b中可以看出，反卷积后的信号相较于原始信号来说，信号之间的混叠减少，甚至可以从信号中辨认出该信号是由两个波组成.相应的，图2c和图2d分别对应着由图2b中两个信号重建的图像.原始信号重建出的图像中两个目标点从视觉上是粘连的.经过反卷积处理，在反卷积后的信号重建出的图像中，两个目标点基本被分开，易于辨认.另外，图2d中每个点相比于图2c中的点更小一些，与图2a中设定的尺寸更接近.

2.2　仿体和活体实验

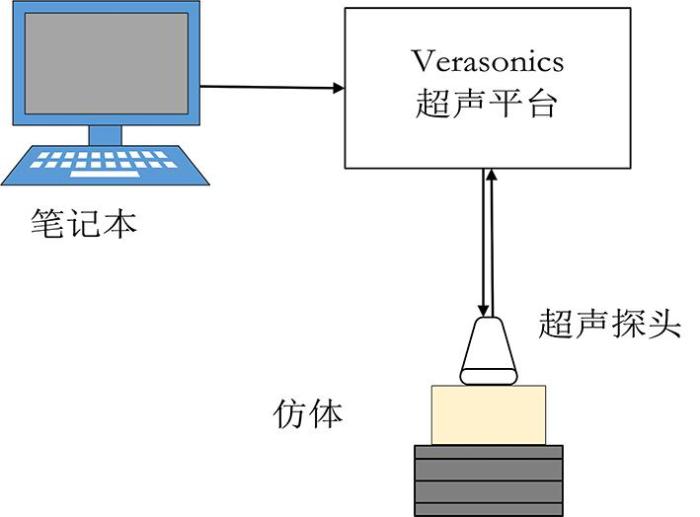
超声实验装置示意图如图3所示.超声实验在Verasonics超声平台上进行.声波发射源有两种发射方式，分别是Flash平面波方式和RyLns方式，其中RyLns方式是一种可调节聚焦深度的宽束方式.本文超声实验使用了两种超声探头，分别是L7⁃4（线性阵列，128个阵元，5.208 MHz中心频率，0.298 mm阵元间隔）和CL15⁃7（线性阵列，128个阵元，9 MHz中心频率，0.178 mm阵元间隔）.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 超声成像实验装置示意图

Fig.3 Diagram of ultrasonic imaging experimental device

超声探头L7⁃4为128个阵元组成的中心频率为5.208 MHz的线性超声相控阵.根据公式计算，该探头可检测的最小尺寸为0.297 mm，实验采用Flash平面波发射接收方式，所有阵元同时发出声波，所有阵元都进行接收.使用直径0.3 mm钨丝为成像目标进行反卷积核的实测.将用L7⁃4对直径0.3 mm钨丝采集的信号归一化后的形状如图4a所示，该信号将作为使用L7⁃4超声探头进行的超声实验的反卷积核.

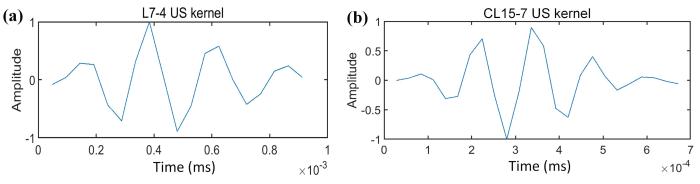
图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 超声实验的归一化的反卷积核：(a) L7⁃4探头；(b) CL15⁃7探头

Fig.4 Normalized deconvolution kernel in ultrasonic experiments：(a) L7⁃4 probe，(b) CL15⁃7 probe

对于实验中的成像目标，本实验将两根直径为2 mm的橡胶条倾斜放置做成模型，两条橡胶条在同一竖直平面上.模型的实拍图如图5a所示.图5a上箭头所指的位置代表采集时探头中心点，基本代表着信号的实际采集位置，可以看到橡胶条之间有一段小于1 mm的间距.采集时是将模型浸没于水中，探头在模型上方与橡胶条平行放置，成像区域为橡胶条所在的竖直平面.

图5

新窗口打开| 下载原图ZIP| 生成PPT

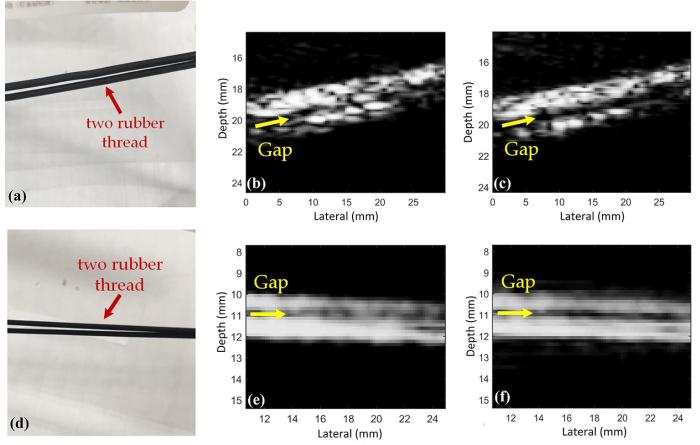
图5 (a) L7⁃4探头成像目标实拍图；(b) L7⁃4探头原始信号重建的图像；(c) L7⁃4探头反卷积后的信号重建的图像；

Fig.5 (a) Real image of imaging target with L7⁃4 probe,(b) reconstructed image of original signals with L7⁃4 probe,(c) reconstructed image of deconvolution signals with L7⁃4 probe,(d) real image of imaging target with CL15⁃7 probe,(e) reconstructed image of original signals with CL15⁃7 probe,(f) reconstructed image of deconvolution signals with CL15⁃7 probe (d) CL15⁃7探头成像目标实拍图；(e) CL15⁃7探头原始信号重建的图像；(f) CL15⁃7探头反卷积后的信号重建的图像

反卷积处理前后的信号重建出的图像对比结果如图5b和图5c所示.图5b是从原始信号重建的图像，由于两根倾斜放置的的橡胶条间距较小，且声信号是从上往下发射，位于上方的橡胶条对于下方的橡胶条有遮挡，图5b中已出现混叠和遮挡，两根线从视觉上看基本没有间隙.如果不预知实验模型的构成，很难从视觉上分辨出结构.但是，在反卷积方法处理后（图5c），处理后的信号重建的图像中两条线之间有了一条明显的间隙，从视觉上是完全分开的，我们可以清晰地识别出这个模型的真实内部结构是两个物体.

超声探头CL15⁃7为128个阵元组成的中心频率为8.929 MHz的线性超声相控阵.根据公式计算，该探头可检测的最小尺寸为0.173 mm.使用CL15⁃7超声探头对直径0.18 mm的铁丝进行信号采集，信号归一化后的形状如图4b所示，该信号将作为使用CL15⁃7超声探头实验的反卷积核.

由于CL15⁃7的中心频率比L7⁃4的中心频率高，可采集到的频带也是更高频的频带，所以适合检测的物体尺寸也更小，所以本节实验采用直径1 mm的两根橡胶条的模型作为采集目标.模型的实拍图如图5d所示.图上箭头所指的位置代表采集时探头中心点所在，基本代表着信号的实际采集位置.

图5e和图5f是用CL15⁃7超声探头以Flash方法采集的原始信号与处理后的反卷积信号分别重建得到的图像的对比.在图5e中，两条线之间有一个模糊的间隙，但并不明显，这是原始信号混叠导致的.图5f在经过反卷积处理后，信号的混叠减轻，相应地图像中的混叠也减少，从视觉上是可以明显看到两条线之间的间隙的.

上述两组仿体实验说明了本文提出的方法对于超声探头具有普适性，并不局限于某种特定型号的超声探头.

在以人体手背为成像目标进行的实验中，使用L7⁃4超声探头，卷积核与图4a一致.采用Flash发射接收方式进行实验，同时以成像效果更好的RyLns发射接收方式所采集的信号重建出的图像作为真值进行验证.

成像目标与采集方式为超声探头与手背垂直放置，成像区域为手背截面，根据解剖学，该成像区域包含多个血管、神经、骨头等.为了给声波提供传输介质，在探头表面与手背接触的位置涂抹了大量的超声耦合剂（透明）作为声传播介质.由于要先按照Flash方式采集一组信号，再按照RyLns方式采集一组信号，两组信号需要采集同一个成像位置，保持成像目标不变，所以在采集过程中要尽量避免成像目标与超声探头的位置移动，因此使用固定架固定住超声探头.

图6a和图6b是本节实验中使用Flash方式采集到的原始信号与反卷积处理后的信号所分别重建出的图像.反卷积后的信号所重建出的图像具有更好的清晰度，且细节信息更清楚，线条边界更明显.图6c~e是图6a和图6b中箭头所指部分的局部放大伪彩图，其中黄色部分为幅值高的部分，蓝色部分为幅值低的部分.

图6

新窗口打开| 下载原图ZIP| 生成PPT

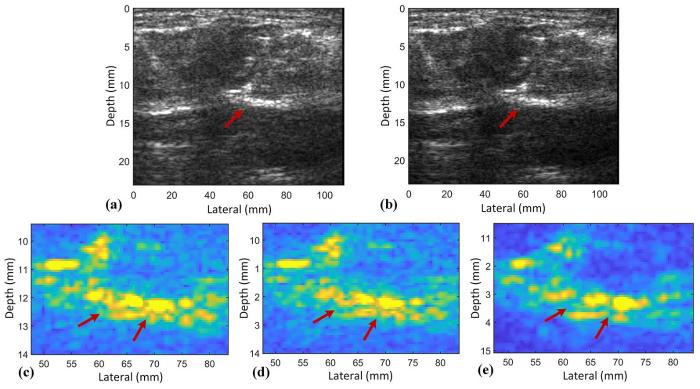
图6 (a) Flash方式采集的原始信号重建的图像；(b) Flash方式采集的反卷积后的信号所重建的图像；(c) Flash方式采集的原始信号重建的局部放大图像；(d) Flash方式采集的反卷积后的信号所重建的局部放大图像；

Fig.6 (a) Image reconstructed by original signals collected by Flash method，(b) image reconstructed by deconvolution signals collected by Flash method，(c) the reconstructed zooming image of original signals collected by Flash，(e) RyLns方式采集的原始信号重建的局部放大图像，(d) the reconstructed zooming image of the deconvolution signals collected by Flash，(e) the reconstructed zooming image of the original signals collected by RyLns

图6e是由RyLns方式进行采集的信号重建出的图像，这种方式的成像效果比Flash好，而且由于聚焦深度可调，所以RyLns发射接收方式对于深度大的成像目标具有更好的成像效果.考虑到该细节位置深度较大，所以采用RyLns方式采集的信号作为一个真值来验证反卷积处理前后的效果.从图6e中可以看出，两个箭头所指位置的成像目标都是有一定间隔的，是相互分开的.在知道这两个组织的结构和相对位置之后，再看图6c和图6d，原始信号重建出的图像中这两个组织之间的间隔不明显，有伪影混叠，但反卷积处理后的信号所重建出的图像中组织之间的间隔变得清晰，可以反映出更加真实的组织结构，所以反卷积后的信号重建出的图像质量更好.

2.3　评价指标量化结果

对于上文中所列出的所有仿真及实验，按照式（5）计算原始信号重建的图像的图像熵与处理后的信号重建的图像的图像熵，对比结果按照之前各个仿真及实验介绍的顺序依次记录在表1中.

表1 仿真与实验中信号处理前后所重建的图像的图像熵对比

Table 1 Image entropy comparison of reconstructed images before and after signal processing in simulation and experiment

组别	原始信号所重建图像的熵	处理后的信号所重建图像的熵
超声仿真	4.5463	4.5097
超声实验1 (L7⁃4，Flash，仿体)	5.3877	5.1408
超声实验2 (CL15⁃7，Flash，仿体)	5.9668	5.5532
超声实验3 (L7⁃4，Flash，活体)	6.1087	5.9886

新窗口打开| 下载CSV

在利用仿体进行的实验中，成像目标为两根倾斜放置的橡胶条，对超声实验1（使用L7⁃4超声探头）和超声实验2（使用CL15⁃7超声探头）视觉可分辨情况进行度量.在平行于橡胶条方向上，逐行统计像素值，并计算每行像素平均值 $P_{i}$ .在超声实验1中，从原始信号重建的超声图像，每行像素平均值 $P_{i}$ 的最小值与重建图像像素最大值比例为25.3%，经过反卷积处理后信号重建的超声图像，每行像素平均值 $P_{i}$ 的最小值与重建图像像素最大值比例为5.2%；在超声实验2中，从原始信号重建的超声图像，每行像素平均值 $P_{i}$ 的最小值与重建图像像素最大值比例为36.9%，经过反卷积处理后的信号重建的超声图像，每行像素平均值 $P_{i}$ 的最小值与重建图像像素最大值比例为17.7%.经过反卷积的超声图像每行像素平均值 $P_{i}$ 均比未处理前有大幅降低，表现在视觉上为两根橡胶条间的间距更清晰.

在选取固定阈值情况下（每行像素平均值 $P_{i}$ 为重建图像像素最大值的40%）统计原始信号重建图像与反卷积处理后信号重建的超声图像中小于阈值的行数之比 $γ$ ，在超声实验1中， $γ_{1} = 1.87$ ；在超声实验2中， $γ_{1} = 1.80$ .在两组实验中，经过反卷积处理的超声图像比原始超声图像可分辨的距离明显提高，表现在视觉上为能够分辨距离更近的目标.

3 结论

超声传感器的激发信号除了受到成像介质的影响，还受到成像方式本身和采集设备不同产生的影响，这种影响是导致超声图像目标混叠和分辨率低的原因之一.针对这个问题，本文提出一种基于反卷积算法的超声图像优化方法，通过实测得到的卷积核对原始采集信号进行处理，利用实测卷积核模拟了信号传递过程中成像方式和采集设备导致的差异性时空传输等效传递函数，实现了超声图像质量优化.通过仿真和实验验证，本文提出的方法可以减轻信号中的混叠，有效减少图像中的遮挡，还原成像目标的真实结构，提高图像分辨率，实现图像优化的目标.实测卷积核的方法具有普适性，对硬件设备无特殊要求.利用卷积核模拟成像中除了成像介质本身对激发信号的影响，同样适用于处理超声图像中影响成像质量的其他问题，具有一定参考价值.本文提出的方法能够有效优化超声图像，使图像结构清楚，利于医生诊断，为超声图像在临床治疗中提供了更广阔的潜在应用前景.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Jensen

J A

, Mathorne

, Gravesen

,et al.

Deconvolution of in⁃vivo ultrasound B⁃mode images

Ultrasonic Imaging,1993,15(2)：122-133. DOI：10.1177/016173469301500204 .