Quantum computers
1
2010
... 量子纠缠作为一种独特的量子资源,其在量子通信、量子计算和量子计量等领域有着重要的作用,可以发挥出经典资源无法比拟的优势[1-3].这种优势近年来越来越多地在实验中被演示和报道[4-8].这种进展得益于量子科技的发展,其中光量子技术起到了关键的作用. ...
Quantum cryptography
0
2002
Advances in quantum metrology
2
2011
... 量子纠缠作为一种独特的量子资源,其在量子通信、量子计算和量子计量等领域有着重要的作用,可以发挥出经典资源无法比拟的优势[1-3].这种优势近年来越来越多地在实验中被演示和报道[4-8].这种进展得益于量子科技的发展,其中光量子技术起到了关键的作用. ...
... 在量子测量和传感领域,可以通过使用纠缠来进一步提高干涉仪和探测设备的灵敏度[3,99].2020年Lu et al[39]利用三维纠缠光量子芯片展示了高维量子纠缠系统出色的相位灵敏度,超过了经典的三路径线性干涉仪和量子二阶非线性干涉仪的极限.2021年,利用Path Identity原理的量子芯片[71]上非区域干涉同样具有相位敏感的特性,结合高维纠缠,可以实现更为灵敏的量子测量和传感器[73].另外,在量子照明原理中[100],维度和纠缠粒子数对灵敏度的增益为,d为纠缠系统的维数,N为纠缠系统粒子数.可以看到,高维纠缠光量子芯片可以在不增加额外光子的情况下实现高集成度和高灵敏度的量子照明雷达光源.随着单光子探测技术的提高,近年来量子照明实验也被报道[101],利用高维纠缠提高增益的演示也有望实现. ...
On the complexity and verification of quantum random circuit sampling
1
2019
... 量子纠缠作为一种独特的量子资源,其在量子通信、量子计算和量子计量等领域有着重要的作用,可以发挥出经典资源无法比拟的优势[1-3].这种优势近年来越来越多地在实验中被演示和报道[4-8].这种进展得益于量子科技的发展,其中光量子技术起到了关键的作用. ...
Quantum supremacy using a programmable superconducting processor
0
2019
Quantum computational advantage using photons
0
2020
Satellite?to?ground quantum key distribution
0
2017
An integrated space?to?ground quantum communication network over 4,600 kilometres
1
2021
... 量子纠缠作为一种独特的量子资源,其在量子通信、量子计算和量子计量等领域有着重要的作用,可以发挥出经典资源无法比拟的优势[1-3].这种优势近年来越来越多地在实验中被演示和报道[4-8].这种进展得益于量子科技的发展,其中光量子技术起到了关键的作用. ...
Precise creation,characterization,and manipulation of single optical qubits
1
2003
... 光子作为量子信息技术的载体有多种优势.它与环境弱耦合,容易实现高保真度的单比特操作[9].另外,光子在传输中有着独特的优势,在需要远距离传输的量子通信网络中发挥重要的作用.同时,多种光量子计算的方法也已经被开发[10-14].然而,不论是量子通信还是各种量子计算策略,产生和操控量子纠缠态都是其中的基础环节. ...
A scheme for efficient quantum computation with linear optics
1
2001
... 光子作为量子信息技术的载体有多种优势.它与环境弱耦合,容易实现高保真度的单比特操作[9].另外,光子在传输中有着独特的优势,在需要远距离传输的量子通信网络中发挥重要的作用.同时,多种光量子计算的方法也已经被开发[10-14].然而,不论是量子通信还是各种量子计算策略,产生和操控量子纠缠态都是其中的基础环节. ...
A one?way quantum computer
0
2001
Measurement?based quantum computation on cluster states
0
2003
Optical quantum computation using cluster states
0
2004
From three?photon Greenberger?Horne?Zeilinger states to ballistic universal quantum computation
1
2015
... 光子作为量子信息技术的载体有多种优势.它与环境弱耦合,容易实现高保真度的单比特操作[9].另外,光子在传输中有着独特的优势,在需要远距离传输的量子通信网络中发挥重要的作用.同时,多种光量子计算的方法也已经被开发[10-14].然而,不论是量子通信还是各种量子计算策略,产生和操控量子纠缠态都是其中的基础环节. ...
Complete experimental toolbox for alignment?free quantum communication
1
... 过去多数被广泛使用的量子协议是基于量子比特的,也就是一个二维量子系统.近年来,人们开始聚焦于高维量子纠缠态.这是因为和二维量子纠缠比较,高维量子纠缠具有独特的优势:首先,高维量子纠缠具有更高的信道容量,能承载更多的信息[15-17];其次,高维量子纠缠有更强的抗噪声能力.这在量子信息的传输过程中尤为重要,主要得益于高维量子纠缠具有更高的纠缠度,具体体现在它对贝尔不等式更大的违反值上[18].另外,基于高维量子纠缠,可以提高许多量子协议的效率和能力,例如实现多用户之间的量子网络[19],提高量子计算和量子模拟的效率[20-22]等. ...
Superdense teleportation using hyperentangled photons
0
Quantum teleportation in high dimensions
1
2019
... 过去多数被广泛使用的量子协议是基于量子比特的,也就是一个二维量子系统.近年来,人们开始聚焦于高维量子纠缠态.这是因为和二维量子纠缠比较,高维量子纠缠具有独特的优势:首先,高维量子纠缠具有更高的信道容量,能承载更多的信息[15-17];其次,高维量子纠缠有更强的抗噪声能力.这在量子信息的传输过程中尤为重要,主要得益于高维量子纠缠具有更高的纠缠度,具体体现在它对贝尔不等式更大的违反值上[18].另外,基于高维量子纠缠,可以提高许多量子协议的效率和能力,例如实现多用户之间的量子网络[19],提高量子计算和量子模拟的效率[20-22]等. ...
Experimental high?dimensional two?photon entanglement and violations of generalized Bell inequalities
1
2011
... 过去多数被广泛使用的量子协议是基于量子比特的,也就是一个二维量子系统.近年来,人们开始聚焦于高维量子纠缠态.这是因为和二维量子纠缠比较,高维量子纠缠具有独特的优势:首先,高维量子纠缠具有更高的信道容量,能承载更多的信息[15-17];其次,高维量子纠缠有更强的抗噪声能力.这在量子信息的传输过程中尤为重要,主要得益于高维量子纠缠具有更高的纠缠度,具体体现在它对贝尔不等式更大的违反值上[18].另外,基于高维量子纠缠,可以提高许多量子协议的效率和能力,例如实现多用户之间的量子网络[19],提高量子计算和量子模拟的效率[20-22]等. ...
Layered quantum key distribution
2
2018
... 过去多数被广泛使用的量子协议是基于量子比特的,也就是一个二维量子系统.近年来,人们开始聚焦于高维量子纠缠态.这是因为和二维量子纠缠比较,高维量子纠缠具有独特的优势:首先,高维量子纠缠具有更高的信道容量,能承载更多的信息[15-17];其次,高维量子纠缠有更强的抗噪声能力.这在量子信息的传输过程中尤为重要,主要得益于高维量子纠缠具有更高的纠缠度,具体体现在它对贝尔不等式更大的违反值上[18].另外,基于高维量子纠缠,可以提高许多量子协议的效率和能力,例如实现多用户之间的量子网络[19],提高量子计算和量子模拟的效率[20-22]等. ...
... 另一方面,在多用户之间建立高维纠缠也是实现多用户之间的量子通信的一种方案[19].同时高维纠缠在量子密钥分发中也可以起到抵御噪声[97]和增强容错率的作用[98],利用集成技术进行高维纠缠产生和调制的芯片也是直接的,可以预见这些量子通信方案的集成化. ...
Simplifying quantum logic using higher?dimensional Hilbert spaces
1
2009
... 过去多数被广泛使用的量子协议是基于量子比特的,也就是一个二维量子系统.近年来,人们开始聚焦于高维量子纠缠态.这是因为和二维量子纠缠比较,高维量子纠缠具有独特的优势:首先,高维量子纠缠具有更高的信道容量,能承载更多的信息[15-17];其次,高维量子纠缠有更强的抗噪声能力.这在量子信息的传输过程中尤为重要,主要得益于高维量子纠缠具有更高的纠缠度,具体体现在它对贝尔不等式更大的违反值上[18].另外,基于高维量子纠缠,可以提高许多量子协议的效率和能力,例如实现多用户之间的量子网络[19],提高量子计算和量子模拟的效率[20-22]等. ...
Large?scale silicon quantum photonics implementing arbitrary two?qubit processing
10
2018
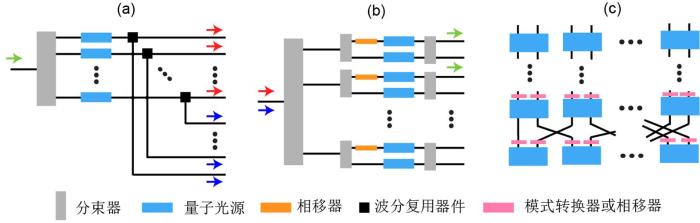
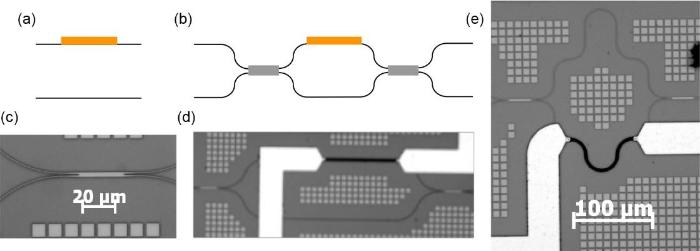
... 在集成量子光学线路中,路径编码因其直接的概念和操作的简易性而颇具吸引力.近年来基于路径编码的二维纠缠光量子芯片[29,36-37]和具有产生和调控高维纠缠光量子态功能的光量子芯片[21,38-39]均已被报道.路径编码和其他编码方式使用的量子光源和调控原理与路径编码是一致的,本综述以发展较为全面的路径编码方式为主干,讨论高维光量子纠缠芯片上高维量子纠缠态产生和调控两个基本功能.下面先从两个部分展开,再介绍高维光量子芯片的应用场景,最后进行总结和展望. ...
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
... 通过将单频泵浦光分束后进入多个SFWM器件利用非简并SFWM过程是目前片上高维纠缠的实验[21,38-39]中所广泛采用的方法.经过量子光源阵列之后光量子态,其中分别为进入第n个量子光源泵浦光的振幅、相位和第n个量子光源的产率,分别为第n个量子光源闲置光子和信号光子的产生算符[43].图4a为一个典型的非简并SFWM过程产生高维纠缠态的量子线路,经过光源阵列后利用波分复用器件将不同频率的信号光子和闲置光子引入不同部分,之后可以通过局域变换和后选择得到目标高维纠缠态. ...
... 图5显示了片上路径编码光量子态的基本操控单元.由相移器和一个MZI结构组成一个二维通用局域线性操作,可以实现任意的SU(2)操作.对两部分的相移器进行控制,对应于旋转块状光学实验中的四分之一玻片和二分之一玻片的角度.相移器主要根据电光原理和热光原理进行相位的控制.通过电光相移器可以获得很高的调制速率[75-76],是未来片上光学调制的发展趋势,但目前部分高速调制依赖于较为苛刻的实验条件[77],并且可能会引起较大的损耗.目前对于产生片上高维纠缠光量子,基于热光相移器的速率已经可以满足基本要求,并且热光调制较为成熟,在近年来的片上高维纠缠光量子实验[21,38-39]中,使用的都是基于热光效应的热光相移器.热光相移器通过由大阻值导电材料(如氮化钛)构成的加热层通电,使加热层发热,引起周围波导温度升高,由于波导材料的折射率随温度变化,导致波导等效折射率的改变,从而引起光子相位的改变. ...
... 另一个基本器件为波分复用器件,对于非简并SFWM,可以通过波分复用器件将信号光子和闲置光子分开.片上高维纠缠光量子实验[21,38-39]中,都是利用这种方式将信号光子和闲置光子分成两路,再对信号光子和闲置光子分别施加局域线性操作.另外,需要片上的波分复用器件将泵浦光尽早滤去,防止在后续较长的光子态操作线路中产生新的光子对,导致噪声引入.片上高维量子纠缠实验一般只需要将信号光子和闲置光子分开,并滤去泵浦光,常用的波分复用器件有光学微腔和不等臂MZI(Asymmetrical Mach–Zehnder Interferometer,AMZI).在早期实验中[29],采用微腔进行滤波,这种方法在理想情况下可以得到较好的消光比,但在实际实验中滤波带宽较窄,由于串扰或者环境扰动使得滤波效果较低且不稳定.AMZI具有较平缓的滤波曲线,鲁棒性较高,相比于共振结构,对温度的敏感性小.近年来,高维纠缠光量子实验[21,38-39]使用了这种波分复用器件.其中四维纠缠光量子芯片[21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
... [21,38-39]使用了这种波分复用器件.其中四维纠缠光量子芯片[21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
... [21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
... 通用操控线路的功能也可大致分为两类:一类是实现任意的单光子局域酉操作,实现SU(N)的变换;另一类是结合后选择实现任意的双光子及多光子门操作.第一类可以对产生的双光子态进行任意的局域酉变换,并通过局域变换对产生的量子态进行量子态断层扫描(Quantum Tomography)[85].在集成三维和十五维光量子芯片实验[38-39]中使用类似的方法来完成高维纠缠光量子的操控和分析,并且采用基于SU(2)单元的酉矩阵线路.实现N维通用局域酉操作一般需要个基本操作单元.随着操作单元的增加,一方面使得操作模块的尺寸增大,另一方面控制的电路和热调器件的复杂度也在增加,电热管理的难度增加.在操控15维的纠缠光子态时[38],采用了只保留信号光子和闲置光子输出部分各一个输出口的方法进行线路简化,相当于从原先的测量一个完整的光子态状态向量,变为每次测量状态向量中的一个元素,这样使芯片上的操作模块的数量降低,需要探测次数相应增加.第二类结合后选择,可以概率性地实现通用双光子量子门(任意双光子酉变换).Qiang et al[21]利用四个酉矩阵的线性组合实现了两光子四维量子门,展示了98个不同的双光子四维量子门,平均操作保真度超过93%.使用的每个四维酉矩阵都由基本操控单元构成,结构简单.使用这类线路可以实现的量子操作大大增加了,与之相对应地,调制器的数量也明显增加.高保真度的多光子高维的通用操作线路也可以实现[86]. ...
... 2018年Qiang et al[21]利用四维纠缠光量子芯片演示了量子近似优化算法(Quantum Approximate Optimization algorithm,QAOA),QAOA可以用来寻找组合搜索问题的近似解,实验中用以解决其中的三个示例约束满足问题(Three Example Constraint Satisfaction Problems,CSPs).同时以在两节点加权图为例,也进行了一类量子游走,即Szegedy量子游走的模拟.2021年,在硅芯片上利用纠缠特性,实现了在任意五顶点图上的纠缠双光子的量子游走[93],展示了对图搜索问题的经典二次加速算法和在多项式时间内判断图同构的量子游走算法. ...
... 相移器数量
输出端口数量 | | 文献[39] | 3×3 | 带有MZI结构的微环共振腔 | AMZI | 任意局域酉操作 | 12 | 6 |
| 文献[21] | 4×4 | 纳米线 | AMZI和MMI | 任意双光子量子门 | 52 | 2 |
| 文献[38] | 15×15 | 纳米线 | AMZI | 任意局域酉操作 | 62 | 2 |
对于未来集成高维光量子芯片的发展,有以下几点展望. ...
Emulation of a quantum spin with a superconducting phase qudit
1
2009
... 过去多数被广泛使用的量子协议是基于量子比特的,也就是一个二维量子系统.近年来,人们开始聚焦于高维量子纠缠态.这是因为和二维量子纠缠比较,高维量子纠缠具有独特的优势:首先,高维量子纠缠具有更高的信道容量,能承载更多的信息[15-17];其次,高维量子纠缠有更强的抗噪声能力.这在量子信息的传输过程中尤为重要,主要得益于高维量子纠缠具有更高的纠缠度,具体体现在它对贝尔不等式更大的违反值上[18].另外,基于高维量子纠缠,可以提高许多量子协议的效率和能力,例如实现多用户之间的量子网络[19],提高量子计算和量子模拟的效率[20-22]等. ...
On?chip generation of high?dimensional entangled quantum states and their coherent control
2
2017
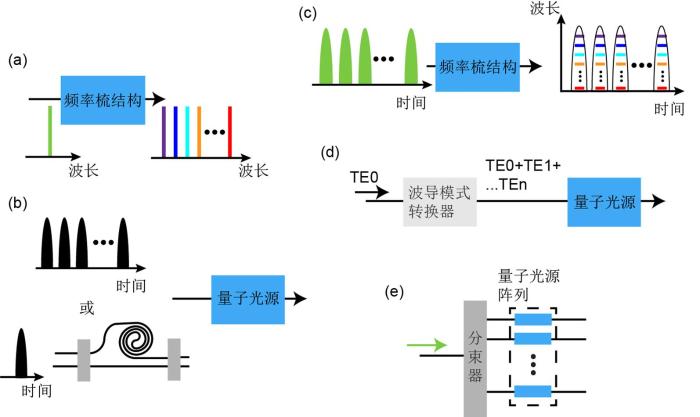
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
50 GHz?spaced comb of high?dimensional frequency?bin entangled photons from an on?chip silicon nitride microresonator
1
2018
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
Frequency?encoded photonic qubits for scalable quantum information processing
2
2017
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
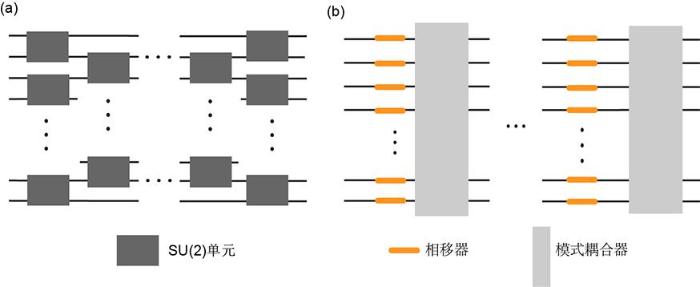
... 实现通用操控线路需要利用可以实现酉矩阵操作的线路.图6为两种主要的片上酉矩阵操作线路的示意图.图6a展示的线路是通过将SU(N)的变换分解为一系列SU(2)的变换来实现的,而任意的SU(2)操作可以被基本操控单元实现,这在块状光学实验中已有报道[79-80],并对使用的干涉器件数量进行了优化[81].Schaeff et al[82]实现了基于此方法的集成三维模块.图6b展示了经典光学芯片研究[83-84]中基于级联相移器和模式耦合器的线路实现方式.在高维光量子态调控中,这种线路实现方法已应用在频率编码中,电光相移器则起到了模式耦合器的作用[25];在路径编码中,模式耦合器可以采用MMI或者DC来实现. ...
Fully arbitrary control of frequency?bin qubits
1
2020
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
Compact and reconfigurable silicon nitride time?bin entanglement circuit
1
2015
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
Integrated silicon nitride time?bin entanglement circuits
0
2018
High?rate photon pairs and sequential Time?Bin entanglement with Si3N4 microring resonators
4
2019
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
... 在集成量子光学线路中,路径编码因其直接的概念和操作的简易性而颇具吸引力.近年来基于路径编码的二维纠缠光量子芯片[29,36-37]和具有产生和调控高维纠缠光量子态功能的光量子芯片[21,38-39]均已被报道.路径编码和其他编码方式使用的量子光源和调控原理与路径编码是一致的,本综述以发展较为全面的路径编码方式为主干,讨论高维光量子纠缠芯片上高维量子纠缠态产生和调控两个基本功能.下面先从两个部分展开,再介绍高维光量子芯片的应用场景,最后进行总结和展望. ...
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
... 另一个基本器件为波分复用器件,对于非简并SFWM,可以通过波分复用器件将信号光子和闲置光子分开.片上高维纠缠光量子实验[21,38-39]中,都是利用这种方式将信号光子和闲置光子分成两路,再对信号光子和闲置光子分别施加局域线性操作.另外,需要片上的波分复用器件将泵浦光尽早滤去,防止在后续较长的光子态操作线路中产生新的光子对,导致噪声引入.片上高维量子纠缠实验一般只需要将信号光子和闲置光子分开,并滤去泵浦光,常用的波分复用器件有光学微腔和不等臂MZI(Asymmetrical Mach–Zehnder Interferometer,AMZI).在早期实验中[29],采用微腔进行滤波,这种方法在理想情况下可以得到较好的消光比,但在实际实验中滤波带宽较窄,由于串扰或者环境扰动使得滤波效果较低且不稳定.AMZI具有较平缓的滤波曲线,鲁棒性较高,相比于共振结构,对温度的敏感性小.近年来,高维纠缠光量子实验[21,38-39]使用了这种波分复用器件.其中四维纠缠光量子芯片[21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
High?dimensional one?way quantum processing implemented on d?level cluster states
2
2019
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
Quantum phase estimation with time?frequency qudits in a single photon
1
2020
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
On?chip transverse?mode entangled photon pair source
1
2019
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
High?dimensional frequency?encoded quantum information processing with passive photonics and time?resolving detection
1
2020
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
Universal programmable on?chip metasurface building blocks for arbitrary high?order mode manipulation
1
2020
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
Multimode silicon photonics
1
2018
... 在光学芯片上可利用多种自由度编码,图1展示了片上产生频率、时间、频率和时间混合、波导模式、路径等自由度纠缠态的制备方法.对于频率编码,基于单个微环谐振腔中多个频率模式相干叠加的方案,可以产生片上高维纠缠光量子态[23-24],并通过级联电光相位调制器和波形整形器(Waveshaper)实现对多个频率梳的并行操控[25-26];对于时间编码,利用输入脉冲序列光信号或者经过片上Franson干涉仪,进入量子光源结构产生时间编码的纠缠光量子态[27-29];也可以将频率和时间维度进行结合,将时间序列泵浦光输入集成频率梳结构,形成频率和时间维度的高维超纠缠,并通过布拉格反射阵列[30]或者啁啾光栅[31],结合循环器和相位调制器线路进行调控;对于波导模式编码,利用片上模式调制器将泵浦光转换为不同波导模式叠加,进入多模波导中产生波导模式编码的纠缠光量子态,片上二维纠缠光量子态已被实现[32].然而,和路径编码比较,这些编码方式在光芯片上主要实现了高维光量子纠缠态的产生部分,在实现片上高保真度、可编程以及任意高维量子调控方面,尽管在原理上已有相关方案[33]和可选用结构被提出[34-35],但实验上依然面临很多困难和挑战. ...
Qubit entanglement between ring?resonator photon?pair sources on a silicon chip
1
2015
... 在集成量子光学线路中,路径编码因其直接的概念和操作的简易性而颇具吸引力.近年来基于路径编码的二维纠缠光量子芯片[29,36-37]和具有产生和调控高维纠缠光量子态功能的光量子芯片[21,38-39]均已被报道.路径编码和其他编码方式使用的量子光源和调控原理与路径编码是一致的,本综述以发展较为全面的路径编码方式为主干,讨论高维光量子纠缠芯片上高维量子纠缠态产生和调控两个基本功能.下面先从两个部分展开,再介绍高维光量子芯片的应用场景,最后进行总结和展望. ...
Silicon photonic processor of two?qubit entangling quantum logic
2
2017
... 在集成量子光学线路中,路径编码因其直接的概念和操作的简易性而颇具吸引力.近年来基于路径编码的二维纠缠光量子芯片[29,36-37]和具有产生和调控高维纠缠光量子态功能的光量子芯片[21,38-39]均已被报道.路径编码和其他编码方式使用的量子光源和调控原理与路径编码是一致的,本综述以发展较为全面的路径编码方式为主干,讨论高维光量子纠缠芯片上高维量子纠缠态产生和调控两个基本功能.下面先从两个部分展开,再介绍高维光量子芯片的应用场景,最后进行总结和展望. ...
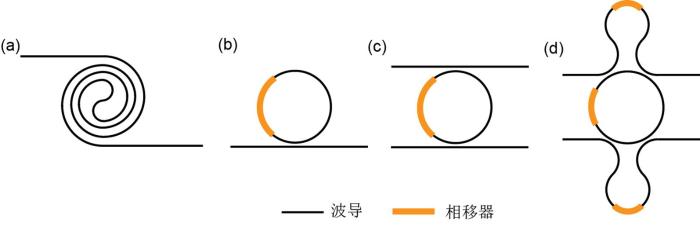
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
Multidimensional quantum entanglement with large?scale integrated optics
12
2018
... 在集成量子光学线路中,路径编码因其直接的概念和操作的简易性而颇具吸引力.近年来基于路径编码的二维纠缠光量子芯片[29,36-37]和具有产生和调控高维纠缠光量子态功能的光量子芯片[21,38-39]均已被报道.路径编码和其他编码方式使用的量子光源和调控原理与路径编码是一致的,本综述以发展较为全面的路径编码方式为主干,讨论高维光量子纠缠芯片上高维量子纠缠态产生和调控两个基本功能.下面先从两个部分展开,再介绍高维光量子芯片的应用场景,最后进行总结和展望. ...
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
... [38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
... [38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
... 通过将单频泵浦光分束后进入多个SFWM器件利用非简并SFWM过程是目前片上高维纠缠的实验[21,38-39]中所广泛采用的方法.经过量子光源阵列之后光量子态,其中分别为进入第n个量子光源泵浦光的振幅、相位和第n个量子光源的产率,分别为第n个量子光源闲置光子和信号光子的产生算符[43].图4a为一个典型的非简并SFWM过程产生高维纠缠态的量子线路,经过光源阵列后利用波分复用器件将不同频率的信号光子和闲置光子引入不同部分,之后可以通过局域变换和后选择得到目标高维纠缠态. ...
... 图5显示了片上路径编码光量子态的基本操控单元.由相移器和一个MZI结构组成一个二维通用局域线性操作,可以实现任意的SU(2)操作.对两部分的相移器进行控制,对应于旋转块状光学实验中的四分之一玻片和二分之一玻片的角度.相移器主要根据电光原理和热光原理进行相位的控制.通过电光相移器可以获得很高的调制速率[75-76],是未来片上光学调制的发展趋势,但目前部分高速调制依赖于较为苛刻的实验条件[77],并且可能会引起较大的损耗.目前对于产生片上高维纠缠光量子,基于热光相移器的速率已经可以满足基本要求,并且热光调制较为成熟,在近年来的片上高维纠缠光量子实验[21,38-39]中,使用的都是基于热光效应的热光相移器.热光相移器通过由大阻值导电材料(如氮化钛)构成的加热层通电,使加热层发热,引起周围波导温度升高,由于波导材料的折射率随温度变化,导致波导等效折射率的改变,从而引起光子相位的改变. ...
... 另一个基本器件为波分复用器件,对于非简并SFWM,可以通过波分复用器件将信号光子和闲置光子分开.片上高维纠缠光量子实验[21,38-39]中,都是利用这种方式将信号光子和闲置光子分成两路,再对信号光子和闲置光子分别施加局域线性操作.另外,需要片上的波分复用器件将泵浦光尽早滤去,防止在后续较长的光子态操作线路中产生新的光子对,导致噪声引入.片上高维量子纠缠实验一般只需要将信号光子和闲置光子分开,并滤去泵浦光,常用的波分复用器件有光学微腔和不等臂MZI(Asymmetrical Mach–Zehnder Interferometer,AMZI).在早期实验中[29],采用微腔进行滤波,这种方法在理想情况下可以得到较好的消光比,但在实际实验中滤波带宽较窄,由于串扰或者环境扰动使得滤波效果较低且不稳定.AMZI具有较平缓的滤波曲线,鲁棒性较高,相比于共振结构,对温度的敏感性小.近年来,高维纠缠光量子实验[21,38-39]使用了这种波分复用器件.其中四维纠缠光量子芯片[21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
... ,38-39]使用了这种波分复用器件.其中四维纠缠光量子芯片[21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
... 通用操控线路的功能也可大致分为两类:一类是实现任意的单光子局域酉操作,实现SU(N)的变换;另一类是结合后选择实现任意的双光子及多光子门操作.第一类可以对产生的双光子态进行任意的局域酉变换,并通过局域变换对产生的量子态进行量子态断层扫描(Quantum Tomography)[85].在集成三维和十五维光量子芯片实验[38-39]中使用类似的方法来完成高维纠缠光量子的操控和分析,并且采用基于SU(2)单元的酉矩阵线路.实现N维通用局域酉操作一般需要个基本操作单元.随着操作单元的增加,一方面使得操作模块的尺寸增大,另一方面控制的电路和热调器件的复杂度也在增加,电热管理的难度增加.在操控15维的纠缠光子态时[38],采用了只保留信号光子和闲置光子输出部分各一个输出口的方法进行线路简化,相当于从原先的测量一个完整的光子态状态向量,变为每次测量状态向量中的一个元素,这样使芯片上的操作模块的数量降低,需要探测次数相应增加.第二类结合后选择,可以概率性地实现通用双光子量子门(任意双光子酉变换).Qiang et al[21]利用四个酉矩阵的线性组合实现了两光子四维量子门,展示了98个不同的双光子四维量子门,平均操作保真度超过93%.使用的每个四维酉矩阵都由基本操控单元构成,结构简单.使用这类线路可以实现的量子操作大大增加了,与之相对应地,调制器的数量也明显增加.高保真度的多光子高维的通用操作线路也可以实现[86]. ...
... [38],采用了只保留信号光子和闲置光子输出部分各一个输出口的方法进行线路简化,相当于从原先的测量一个完整的光子态状态向量,变为每次测量状态向量中的一个元素,这样使芯片上的操作模块的数量降低,需要探测次数相应增加.第二类结合后选择,可以概率性地实现通用双光子量子门(任意双光子酉变换).Qiang et al[21]利用四个酉矩阵的线性组合实现了两光子四维量子门,展示了98个不同的双光子四维量子门,平均操作保真度超过93%.使用的每个四维酉矩阵都由基本操控单元构成,结构简单.使用这类线路可以实现的量子操作大大增加了,与之相对应地,调制器的数量也明显增加.高保真度的多光子高维的通用操作线路也可以实现[86]. ...
... 进一步地,更高维度的纠缠光量子芯片[38]开始探索一些以前未探索的量子应用,例如量子随机性扩展和多维状态的自测试,这显示了集成高维纠缠光量子芯片的巨大潜力. ...
... 相移器数量
输出端口数量 | | 文献[39] | 3×3 | 带有MZI结构的微环共振腔 | AMZI | 任意局域酉操作 | 12 | 6 |
| 文献[21] | 4×4 | 纳米线 | AMZI和MMI | 任意双光子量子门 | 52 | 2 |
| 文献[38] | 15×15 | 纳米线 | AMZI | 任意局域酉操作 | 62 | 2 |
对于未来集成高维光量子芯片的发展,有以下几点展望. ...
Three?dimensional entanglement on a silicon chip
10
2020
... 在集成量子光学线路中,路径编码因其直接的概念和操作的简易性而颇具吸引力.近年来基于路径编码的二维纠缠光量子芯片[29,36-37]和具有产生和调控高维纠缠光量子态功能的光量子芯片[21,38-39]均已被报道.路径编码和其他编码方式使用的量子光源和调控原理与路径编码是一致的,本综述以发展较为全面的路径编码方式为主干,讨论高维光量子纠缠芯片上高维量子纠缠态产生和调控两个基本功能.下面先从两个部分展开,再介绍高维光量子芯片的应用场景,最后进行总结和展望. ...
... 通过将单频泵浦光分束后进入多个SFWM器件利用非简并SFWM过程是目前片上高维纠缠的实验[21,38-39]中所广泛采用的方法.经过量子光源阵列之后光量子态,其中分别为进入第n个量子光源泵浦光的振幅、相位和第n个量子光源的产率,分别为第n个量子光源闲置光子和信号光子的产生算符[43].图4a为一个典型的非简并SFWM过程产生高维纠缠态的量子线路,经过光源阵列后利用波分复用器件将不同频率的信号光子和闲置光子引入不同部分,之后可以通过局域变换和后选择得到目标高维纠缠态. ...
... 图5显示了片上路径编码光量子态的基本操控单元.由相移器和一个MZI结构组成一个二维通用局域线性操作,可以实现任意的SU(2)操作.对两部分的相移器进行控制,对应于旋转块状光学实验中的四分之一玻片和二分之一玻片的角度.相移器主要根据电光原理和热光原理进行相位的控制.通过电光相移器可以获得很高的调制速率[75-76],是未来片上光学调制的发展趋势,但目前部分高速调制依赖于较为苛刻的实验条件[77],并且可能会引起较大的损耗.目前对于产生片上高维纠缠光量子,基于热光相移器的速率已经可以满足基本要求,并且热光调制较为成熟,在近年来的片上高维纠缠光量子实验[21,38-39]中,使用的都是基于热光效应的热光相移器.热光相移器通过由大阻值导电材料(如氮化钛)构成的加热层通电,使加热层发热,引起周围波导温度升高,由于波导材料的折射率随温度变化,导致波导等效折射率的改变,从而引起光子相位的改变. ...
... 另一个基本器件为波分复用器件,对于非简并SFWM,可以通过波分复用器件将信号光子和闲置光子分开.片上高维纠缠光量子实验[21,38-39]中,都是利用这种方式将信号光子和闲置光子分成两路,再对信号光子和闲置光子分别施加局域线性操作.另外,需要片上的波分复用器件将泵浦光尽早滤去,防止在后续较长的光子态操作线路中产生新的光子对,导致噪声引入.片上高维量子纠缠实验一般只需要将信号光子和闲置光子分开,并滤去泵浦光,常用的波分复用器件有光学微腔和不等臂MZI(Asymmetrical Mach–Zehnder Interferometer,AMZI).在早期实验中[29],采用微腔进行滤波,这种方法在理想情况下可以得到较好的消光比,但在实际实验中滤波带宽较窄,由于串扰或者环境扰动使得滤波效果较低且不稳定.AMZI具有较平缓的滤波曲线,鲁棒性较高,相比于共振结构,对温度的敏感性小.近年来,高维纠缠光量子实验[21,38-39]使用了这种波分复用器件.其中四维纠缠光量子芯片[21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
... -39]使用了这种波分复用器件.其中四维纠缠光量子芯片[21]在分开信号光子和闲置光子时直接利用MMI结合片外滤波,这会引入额外的损耗,但是和之前的方法比较,不需要进行外部信号的调制,减小了调制的压力. ...
... 通用操控线路的功能也可大致分为两类:一类是实现任意的单光子局域酉操作,实现SU(N)的变换;另一类是结合后选择实现任意的双光子及多光子门操作.第一类可以对产生的双光子态进行任意的局域酉变换,并通过局域变换对产生的量子态进行量子态断层扫描(Quantum Tomography)[85].在集成三维和十五维光量子芯片实验[38-39]中使用类似的方法来完成高维纠缠光量子的操控和分析,并且采用基于SU(2)单元的酉矩阵线路.实现N维通用局域酉操作一般需要个基本操作单元.随着操作单元的增加,一方面使得操作模块的尺寸增大,另一方面控制的电路和热调器件的复杂度也在增加,电热管理的难度增加.在操控15维的纠缠光子态时[38],采用了只保留信号光子和闲置光子输出部分各一个输出口的方法进行线路简化,相当于从原先的测量一个完整的光子态状态向量,变为每次测量状态向量中的一个元素,这样使芯片上的操作模块的数量降低,需要探测次数相应增加.第二类结合后选择,可以概率性地实现通用双光子量子门(任意双光子酉变换).Qiang et al[21]利用四个酉矩阵的线性组合实现了两光子四维量子门,展示了98个不同的双光子四维量子门,平均操作保真度超过93%.使用的每个四维酉矩阵都由基本操控单元构成,结构简单.使用这类线路可以实现的量子操作大大增加了,与之相对应地,调制器的数量也明显增加.高保真度的多光子高维的通用操作线路也可以实现[86]. ...
... 高维纠缠光量子芯片上不可避免地具有较多的调制器件,由于目前相移器主要采用热调控器件,每个热调控器件大约需要消耗微瓦量级的功率,这使芯片上的热管理成为一个必须要面对的问题.热管理对采用了微环共振腔作为光子对源的芯片十分关键[39],因为共振结构对温度十分敏感,各个微环受热不相等时,会使不同微环中共振峰出现不同程度的平移,导致光源的不可分辨性被破坏,造成量子态的纯度降低.除了2.1和2.2中提到的设计方法可以降低器件的热敏感度以及减小热调制器件的数量外,也可以通过设计调制器件的方法来克服热串扰.Harris et al[87]设计了不同掺杂浓度的电阻截面使电流传输垂直于波导获得局域性发热和减小热串扰.Gao et al[88]通过独立的条形波导并部分挖空衬底的方式实现了具有高效但显著热隔离的调制.Jacques et al[89]采用热调器件之间进行刻蚀和结构优化的方法减小调制器之间的热串扰. ...
... 2017年Krenn et al[90]发现了图与高维量子纠缠实验一一对应的关系,并由此提出了一种利用高维量子纠缠实验线路对图进行模拟的方法,通过测量与给定图的对应的量子线路产生的量子态的项数,可以得到目标图的完美匹配数,而计算给定图的完美匹配数的算法复杂度是#P完全的[91],2020年,利用三维纠缠光量子态模拟对两个顶点三条边的图已由三维纠缠光量子芯片展示[39].2019年Gu et al[92]扩展了图与量子纠缠实验的对应关系,引入相位和权重.基于这种扩展关系,可以解决更多困难的图论问题,例如对复杂加权图完美匹配权重求和,这也是一个#P完全的问题.2021年Feng et al[71]展示的四光子非区域干涉现象,是这种扩展关系的芯片实现,对应一个四顶点四边图.在此基础上,在芯片上引入更多高维纠缠可以实现更丰富的量子模拟. ...
... 在量子测量和传感领域,可以通过使用纠缠来进一步提高干涉仪和探测设备的灵敏度[3,99].2020年Lu et al[39]利用三维纠缠光量子芯片展示了高维量子纠缠系统出色的相位灵敏度,超过了经典的三路径线性干涉仪和量子二阶非线性干涉仪的极限.2021年,利用Path Identity原理的量子芯片[71]上非区域干涉同样具有相位敏感的特性,结合高维纠缠,可以实现更为灵敏的量子测量和传感器[73].另外,在量子照明原理中[100],维度和纠缠粒子数对灵敏度的增益为,d为纠缠系统的维数,N为纠缠系统粒子数.可以看到,高维纠缠光量子芯片可以在不增加额外光子的情况下实现高集成度和高灵敏度的量子照明雷达光源.随着单光子探测技术的提高,近年来量子照明实验也被报道[101],利用高维纠缠提高增益的演示也有望实现. ...
... 相移器数量
输出端口数量 | | 文献[39] | 3×3 | 带有MZI结构的微环共振腔 | AMZI | 任意局域酉操作 | 12 | 6 |
| 文献[21] | 4×4 | 纳米线 | AMZI和MMI | 任意双光子量子门 | 52 | 2 |
| 文献[38] | 15×15 | 纳米线 | AMZI | 任意局域酉操作 | 62 | 2 |
对于未来集成高维光量子芯片的发展,有以下几点展望. ...
Ultrabright multiplexed energy?time?entangled photon generation from lithium niobate on insulator chip
1
2021
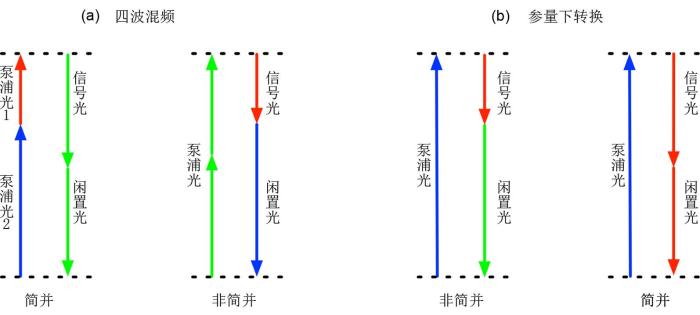
... SPDC过程在光学芯片上可由准相位匹配技术实现,比如在LNOI(Lithium Niobate on Insulator)平台上实现[40-43].对于广泛使用的硅光芯片,由于硅晶体的中心对称结构,硅波导没有二阶非线性系数而具有较大的三阶非线性系数,因此SFWM是硅光芯片上产生光子对的有效方式,也是目前高维纠缠光量子芯片所普遍采用的方法.并且,在SFWM中非简并过程产生光子对的产率要高于简并过程[43]. ...
Ultrabright quantum photon sources on chip
1
2020
... 与之相对的,光学微腔具有更高的集成度;在路径编码中,相位匹配条件很容易得到满足;在频率编码中,可以通过微腔截面的设计对微腔内群速度色散进行调制[55],使得产生的信号光子和闲置光子具有多个频率分量,形成量子频率梳;共振腔的滤波特性会产生窄带宽的光子对,并且共振腔的场增强效应在泵浦光一样的情况下可以获得比纳米线高得多的产率[41,57-61].这些特性使得光学共振微腔成为产生片上集成高维纠缠光子的理想光源.光学微腔的一个重要指标是它的品质因子Q(Quality Factor),光学微腔总的Q值由两部分构成,内部(Qi)和外部(Qe)[62].Qi与微腔内损耗因子有关,Qe与微腔与波导之间的耦合系数有关.总的Q值反映了微腔的滤波带宽,Qi和Qe共同决定了微腔的消光比和光子对的产率与亮度[63].对于,和三种情况,对应损耗因子大于、等于和小于耦合系数,分别被称为过耦(Over Coupling)合、关键(临界)耦合(Critical Coupling)和弱耦合(Under Coupling). ...
High quality entangled photon pair generation in periodically poled thin?film lithium niobate waveguides
0
2020
4
2015
... SPDC过程在光学芯片上可由准相位匹配技术实现,比如在LNOI(Lithium Niobate on Insulator)平台上实现[40-43].对于广泛使用的硅光芯片,由于硅晶体的中心对称结构,硅波导没有二阶非线性系数而具有较大的三阶非线性系数,因此SFWM是硅光芯片上产生光子对的有效方式,也是目前高维纠缠光量子芯片所普遍采用的方法.并且,在SFWM中非简并过程产生光子对的产率要高于简并过程[43]. ...
... [43]. ...
... 通过将单频泵浦光分束后进入多个SFWM器件利用非简并SFWM过程是目前片上高维纠缠的实验[21,38-39]中所广泛采用的方法.经过量子光源阵列之后光量子态,其中分别为进入第n个量子光源泵浦光的振幅、相位和第n个量子光源的产率,分别为第n个量子光源闲置光子和信号光子的产生算符[43].图4a为一个典型的非简并SFWM过程产生高维纠缠态的量子线路,经过光源阵列后利用波分复用器件将不同频率的信号光子和闲置光子引入不同部分,之后可以通过局域变换和后选择得到目标高维纠缠态. ...
... 目前高维纠缠光量子芯片采用直流电信号进行调制,电串扰主要由芯片上地级与电源之间的电势差引起,可以利用负反馈电路排除电串扰[43].由于此类电串扰的原因是两个地级之间存在额外电阻分压,也可以用电流源替代电压源来解决这一问题. ...
Heralding two?photon and four?photon path entanglement on a chip
1
2011
... 另一种“非线性过程”是对量子态的后选择来实现的,即要求测量必须包括指定的输出状态,包括预报(Heralding)[44-45]和光子符合(Coincidence)[46-47],这也是目前片上高维光量子纠缠态产生的普遍方法. ...
Integrated frequency comb source of heralded single photons
1
2014
... 另一种“非线性过程”是对量子态的后选择来实现的,即要求测量必须包括指定的输出状态,包括预报(Heralding)[44-45]和光子符合(Coincidence)[46-47],这也是目前片上高维光量子纠缠态产生的普遍方法. ...
Controlling the degree of visibility of Young's fringes with photon coincidence measurements
1
1994
... 另一种“非线性过程”是对量子态的后选择来实现的,即要求测量必须包括指定的输出状态,包括预报(Heralding)[44-45]和光子符合(Coincidence)[46-47],这也是目前片上高维光量子纠缠态产生的普遍方法. ...
Linear optical controlled?NOT gate in the coincidence basis
1
2002
... 另一种“非线性过程”是对量子态的后选择来实现的,即要求测量必须包括指定的输出状态,包括预报(Heralding)[44-45]和光子符合(Coincidence)[46-47],这也是目前片上高维光量子纠缠态产生的普遍方法. ...
Ultrabroadband parametric generation and wavelength conversion in silicon waveguides
1
2006
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
Nonlinear optical phenomena in silicon waveguides:Modeling and applications
2
2007
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
Phase regeneration of DPSK signals in a silicon waveguide with reverse?biased p?i?n junction
1
2014
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
Mid?infrared quantum optics in silicon
1
2020
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
Silicon?nitride platform for narrowband entangled photon generation
1
2015
... 除此之外,还存在对产生纠缠光量子不利的非线性因素,如拉曼散射(Raman Scatter)、自由载流子吸收(Free Carrier Absorption)和双光子吸收(Two⁃Photon Absorption).对于硅材料,距泵浦15.6 THz处产生的窄带拉曼噪声可通过选取合适的泵浦波长和滤波进行抑制[48-49].利用p⁃i⁃n结减小自由载流子吸收的方法也被报道[50].对于硅材料中的双光子吸收效应,一方面,可以通过改进量子光源结构(2.2)或者在带隙对于双光子吸收难以产生的区域选择泵浦波长[51]减弱该效应的影响;另一方面,可以选择氮化硅[29,52]和高折射率掺杂二氧化硅(Hydex)[23,30]材料,它们没有双光子吸收并且具有较小的损耗. ...
On?chip quantum interference between silicon photon?pair sources
1
2014
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
An entanglement?based wavelength?multiplexed quantum communication network
2
2018
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
... 高维纠缠可以在量子通信网络中发挥巨大作用.2018年Wengerowsky et al [54]利用块状光学产生的高维频率纠缠结合波分复用器件来建立多用户之间的量子秘钥分发网络.2020年,该方案用于改进用户之间的连接方式,Liu et al[94]和Joshi et al[95]将其进一步优化和扩展,用户数量显著提升.2021年,也报道了利用片上产生的纠缠光源实现的量子通信网络[96]. ...
Frequency?bin entangled comb of photon pairs from a silicon?on?insulator micro?resonator
2
2011
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
... 与之相对的,光学微腔具有更高的集成度;在路径编码中,相位匹配条件很容易得到满足;在频率编码中,可以通过微腔截面的设计对微腔内群速度色散进行调制[55],使得产生的信号光子和闲置光子具有多个频率分量,形成量子频率梳;共振腔的滤波特性会产生窄带宽的光子对,并且共振腔的场增强效应在泵浦光一样的情况下可以获得比纳米线高得多的产率[41,57-61].这些特性使得光学共振微腔成为产生片上集成高维纠缠光子的理想光源.光学微腔的一个重要指标是它的品质因子Q(Quality Factor),光学微腔总的Q值由两部分构成,内部(Qi)和外部(Qe)[62].Qi与微腔内损耗因子有关,Qe与微腔与波导之间的耦合系数有关.总的Q值反映了微腔的滤波带宽,Qi和Qe共同决定了微腔的消光比和光子对的产率与亮度[63].对于,和三种情况,对应损耗因子大于、等于和小于耦合系数,分别被称为过耦(Over Coupling)合、关键(临界)耦合(Critical Coupling)和弱耦合(Under Coupling). ...
Multi?photon absorption limits to heralded single photon sources
1
2013
... 图3展示近年来被报道的实验中使用的产生纠缠光子对的片上纠缠光源.产生光子对的集成光源最主要有纳米线(长波导,图3a)和光学微环腔(图3b、图3c和图3d)两种.为了得到相对较高产率的光子对,常常需要几毫米到几十厘米长的波导[21,37-38,53],这导致集成性的降低,同时由于相位匹配的范围较大,容易产生宽谱的光子对[38].宽谱的光子对可以通过滤波器产生高维频率编码的纠缠光子对,这可以用于多用户的量子密钥分发实验中[54].然而,对于产生路径编码的高维纠缠态,为了获得高纯度的量子态和保证不可分辨性,操作和探测时往往只利用其中较窄的带宽,这需要在片上或者片外利用滤波器将特定波长的光滤出[38],会导致相当一部分光被浪费,从而使得产率降低.产生光子对的频率带宽可以通过对波导的群速度调制来缩小,这需要通过对波导横截面进行设计[55].另外,纳米线获得光子对高产率往往也需要高的泵浦光强度,由于较高的光强在硅中会产生双光子吸收等非线性效应[49,56],这会限制硅纳米线的光子对产率. ...
Photon pair generation in a silicon micro?ring resonator with reverse bias enhancement
1
2013
... 与之相对的,光学微腔具有更高的集成度;在路径编码中,相位匹配条件很容易得到满足;在频率编码中,可以通过微腔截面的设计对微腔内群速度色散进行调制[55],使得产生的信号光子和闲置光子具有多个频率分量,形成量子频率梳;共振腔的滤波特性会产生窄带宽的光子对,并且共振腔的场增强效应在泵浦光一样的情况下可以获得比纳米线高得多的产率[41,57-61].这些特性使得光学共振微腔成为产生片上集成高维纠缠光子的理想光源.光学微腔的一个重要指标是它的品质因子Q(Quality Factor),光学微腔总的Q值由两部分构成,内部(Qi)和外部(Qe)[62].Qi与微腔内损耗因子有关,Qe与微腔与波导之间的耦合系数有关.总的Q值反映了微腔的滤波带宽,Qi和Qe共同决定了微腔的消光比和光子对的产率与亮度[63].对于,和三种情况,对应损耗因子大于、等于和小于耦合系数,分别被称为过耦(Over Coupling)合、关键(临界)耦合(Critical Coupling)和弱耦合(Under Coupling). ...
Generation of multiphoton entangled quantum states by means of integrated frequency combs
0
2016
Path to increasing the coincidence efficiency of integrated resonant photon sources
1
2017
... 图3b、图3c和图3d展示了产生纠缠光子对实验中用到的作为量子光源的三种微环腔.单波导微环是结构最简单的一种微环共振腔,为了获得最高的光子对产率和亮度,单波导微环需要的耦合类型分别为过耦合和关键耦合[64].由于波导损耗和耦合系数都非常依赖于加工过程,很难做到完全符合预期,而且Qi与Qe非常依赖这两个参数,这会极大地影响集成光源的光子对产率[65].为了消除加工过程对产率的影响,Strain et al[65]在耦合区域增加调制器件,使微环共振腔的Q值可调,从而克服加工中的不确定性.另一方面,也可以采用双波导微环来克服这一问题,这是由于引入第二条波导的耦合,在波导损耗很小的情况下,等效的损耗因子与第一条波导和环之间的耦合系数近似相等,从而达到关键耦合的条件.不过,这些方法虽然增加了光子对的产率和产率的稳定性,但是对于传统的微腔,光子对亮度提高的同时,光子对的预报率(Heralding Efficiency)或收集率会下降[66].对于单波导微环,在关键耦合时获得最高的光子对亮度,此时,对应于损耗因子与耦合系数相等.这意味着,在腔内产生的一对光子,每个光子都有50%的概率在腔内损耗或者是耦合到出射波导中,再考虑到出射波导到探测器之间的损耗,接收到一对光子对的概率至多为25%.类似地,在关键耦合时,对于双波导环,每个产生的光子有50%概率在腔内损耗和从第二条波导出射或者50%概率从第一条波导出射,从一条波导收集到两个光子的概率最高为25%.为了解决这一问题,可以利用带有马赫⁃曾德尔干涉仪(Mach–Zehnder Interferometer,MZI)的微环共振腔[59,67].加入输入和输出端的干涉结构后,输入端对于泵浦光为关键耦合,只允许泵浦光进入微环,而不能从任一端耦合出微环,这保证了光子对的产率和高亮度,同时对于产生的信号光子和闲置光子,只允许在输出端被耦出,保证了较高的收集效率.通过改进,可以在获得高产率和亮度的同时获得高的收集效率.不仅如此,由于带有MZI干涉结构的微环可以调节输入(输出)波导和微环之间的耦合系数,从而对微环的Q值进行调制,克服加工因素的影响;此外,因为输出端的干涉结构对泵浦光进行了一次滤波,所以可以减轻腔外滤波的需求. ...
Chip?integrated visible–telecom entangled photon pair source for quantum communication
1
2019
... 与之相对的,光学微腔具有更高的集成度;在路径编码中,相位匹配条件很容易得到满足;在频率编码中,可以通过微腔截面的设计对微腔内群速度色散进行调制[55],使得产生的信号光子和闲置光子具有多个频率分量,形成量子频率梳;共振腔的滤波特性会产生窄带宽的光子对,并且共振腔的场增强效应在泵浦光一样的情况下可以获得比纳米线高得多的产率[41,57-61].这些特性使得光学共振微腔成为产生片上集成高维纠缠光子的理想光源.光学微腔的一个重要指标是它的品质因子Q(Quality Factor),光学微腔总的Q值由两部分构成,内部(Qi)和外部(Qe)[62].Qi与微腔内损耗因子有关,Qe与微腔与波导之间的耦合系数有关.总的Q值反映了微腔的滤波带宽,Qi和Qe共同决定了微腔的消光比和光子对的产率与亮度[63].对于,和三种情况,对应损耗因子大于、等于和小于耦合系数,分别被称为过耦(Over Coupling)合、关键(临界)耦合(Critical Coupling)和弱耦合(Under Coupling). ...
Silicon microring resonators
1
2012
... 与之相对的,光学微腔具有更高的集成度;在路径编码中,相位匹配条件很容易得到满足;在频率编码中,可以通过微腔截面的设计对微腔内群速度色散进行调制[55],使得产生的信号光子和闲置光子具有多个频率分量,形成量子频率梳;共振腔的滤波特性会产生窄带宽的光子对,并且共振腔的场增强效应在泵浦光一样的情况下可以获得比纳米线高得多的产率[41,57-61].这些特性使得光学共振微腔成为产生片上集成高维纠缠光子的理想光源.光学微腔的一个重要指标是它的品质因子Q(Quality Factor),光学微腔总的Q值由两部分构成,内部(Qi)和外部(Qe)[62].Qi与微腔内损耗因子有关,Qe与微腔与波导之间的耦合系数有关.总的Q值反映了微腔的滤波带宽,Qi和Qe共同决定了微腔的消光比和光子对的产率与亮度[63].对于,和三种情况,对应损耗因子大于、等于和小于耦合系数,分别被称为过耦(Over Coupling)合、关键(临界)耦合(Critical Coupling)和弱耦合(Under Coupling). ...
The impact of nonlinear losses in the silicon micro?ring cavities on cw pumping correlated photon pair generation
1
2014
... 与之相对的,光学微腔具有更高的集成度;在路径编码中,相位匹配条件很容易得到满足;在频率编码中,可以通过微腔截面的设计对微腔内群速度色散进行调制[55],使得产生的信号光子和闲置光子具有多个频率分量,形成量子频率梳;共振腔的滤波特性会产生窄带宽的光子对,并且共振腔的场增强效应在泵浦光一样的情况下可以获得比纳米线高得多的产率[41,57-61].这些特性使得光学共振微腔成为产生片上集成高维纠缠光子的理想光源.光学微腔的一个重要指标是它的品质因子Q(Quality Factor),光学微腔总的Q值由两部分构成,内部(Qi)和外部(Qe)[62].Qi与微腔内损耗因子有关,Qe与微腔与波导之间的耦合系数有关.总的Q值反映了微腔的滤波带宽,Qi和Qe共同决定了微腔的消光比和光子对的产率与亮度[63].对于,和三种情况,对应损耗因子大于、等于和小于耦合系数,分别被称为过耦(Over Coupling)合、关键(临界)耦合(Critical Coupling)和弱耦合(Under Coupling). ...
Generation rate scaling:The quality factor optimization of microring resonators for photon?pair sources
1
2018
... 图3b、图3c和图3d展示了产生纠缠光子对实验中用到的作为量子光源的三种微环腔.单波导微环是结构最简单的一种微环共振腔,为了获得最高的光子对产率和亮度,单波导微环需要的耦合类型分别为过耦合和关键耦合[64].由于波导损耗和耦合系数都非常依赖于加工过程,很难做到完全符合预期,而且Qi与Qe非常依赖这两个参数,这会极大地影响集成光源的光子对产率[65].为了消除加工过程对产率的影响,Strain et al[65]在耦合区域增加调制器件,使微环共振腔的Q值可调,从而克服加工中的不确定性.另一方面,也可以采用双波导微环来克服这一问题,这是由于引入第二条波导的耦合,在波导损耗很小的情况下,等效的损耗因子与第一条波导和环之间的耦合系数近似相等,从而达到关键耦合的条件.不过,这些方法虽然增加了光子对的产率和产率的稳定性,但是对于传统的微腔,光子对亮度提高的同时,光子对的预报率(Heralding Efficiency)或收集率会下降[66].对于单波导微环,在关键耦合时获得最高的光子对亮度,此时,对应于损耗因子与耦合系数相等.这意味着,在腔内产生的一对光子,每个光子都有50%的概率在腔内损耗或者是耦合到出射波导中,再考虑到出射波导到探测器之间的损耗,接收到一对光子对的概率至多为25%.类似地,在关键耦合时,对于双波导环,每个产生的光子有50%概率在腔内损耗和从第二条波导出射或者50%概率从第一条波导出射,从一条波导收集到两个光子的概率最高为25%.为了解决这一问题,可以利用带有马赫⁃曾德尔干涉仪(Mach–Zehnder Interferometer,MZI)的微环共振腔[59,67].加入输入和输出端的干涉结构后,输入端对于泵浦光为关键耦合,只允许泵浦光进入微环,而不能从任一端耦合出微环,这保证了光子对的产率和高亮度,同时对于产生的信号光子和闲置光子,只允许在输出端被耦出,保证了较高的收集效率.通过改进,可以在获得高产率和亮度的同时获得高的收集效率.不仅如此,由于带有MZI干涉结构的微环可以调节输入(输出)波导和微环之间的耦合系数,从而对微环的Q值进行调制,克服加工因素的影响;此外,因为输出端的干涉结构对泵浦光进行了一次滤波,所以可以减轻腔外滤波的需求. ...
Tunable Q?factor silicon microring resonators for ultra?low power parametric processes
2
2015
... 图3b、图3c和图3d展示了产生纠缠光子对实验中用到的作为量子光源的三种微环腔.单波导微环是结构最简单的一种微环共振腔,为了获得最高的光子对产率和亮度,单波导微环需要的耦合类型分别为过耦合和关键耦合[64].由于波导损耗和耦合系数都非常依赖于加工过程,很难做到完全符合预期,而且Qi与Qe非常依赖这两个参数,这会极大地影响集成光源的光子对产率[65].为了消除加工过程对产率的影响,Strain et al[65]在耦合区域增加调制器件,使微环共振腔的Q值可调,从而克服加工中的不确定性.另一方面,也可以采用双波导微环来克服这一问题,这是由于引入第二条波导的耦合,在波导损耗很小的情况下,等效的损耗因子与第一条波导和环之间的耦合系数近似相等,从而达到关键耦合的条件.不过,这些方法虽然增加了光子对的产率和产率的稳定性,但是对于传统的微腔,光子对亮度提高的同时,光子对的预报率(Heralding Efficiency)或收集率会下降[66].对于单波导微环,在关键耦合时获得最高的光子对亮度,此时,对应于损耗因子与耦合系数相等.这意味着,在腔内产生的一对光子,每个光子都有50%的概率在腔内损耗或者是耦合到出射波导中,再考虑到出射波导到探测器之间的损耗,接收到一对光子对的概率至多为25%.类似地,在关键耦合时,对于双波导环,每个产生的光子有50%概率在腔内损耗和从第二条波导出射或者50%概率从第一条波导出射,从一条波导收集到两个光子的概率最高为25%.为了解决这一问题,可以利用带有马赫⁃曾德尔干涉仪(Mach–Zehnder Interferometer,MZI)的微环共振腔[59,67].加入输入和输出端的干涉结构后,输入端对于泵浦光为关键耦合,只允许泵浦光进入微环,而不能从任一端耦合出微环,这保证了光子对的产率和高亮度,同时对于产生的信号光子和闲置光子,只允许在输出端被耦出,保证了较高的收集效率.通过改进,可以在获得高产率和亮度的同时获得高的收集效率.不仅如此,由于带有MZI干涉结构的微环可以调节输入(输出)波导和微环之间的耦合系数,从而对微环的Q值进行调制,克服加工因素的影响;此外,因为输出端的干涉结构对泵浦光进行了一次滤波,所以可以减轻腔外滤波的需求. ...
... [65]在耦合区域增加调制器件,使微环共振腔的Q值可调,从而克服加工中的不确定性.另一方面,也可以采用双波导微环来克服这一问题,这是由于引入第二条波导的耦合,在波导损耗很小的情况下,等效的损耗因子与第一条波导和环之间的耦合系数近似相等,从而达到关键耦合的条件.不过,这些方法虽然增加了光子对的产率和产率的稳定性,但是对于传统的微腔,光子对亮度提高的同时,光子对的预报率(Heralding Efficiency)或收集率会下降[66].对于单波导微环,在关键耦合时获得最高的光子对亮度,此时,对应于损耗因子与耦合系数相等.这意味着,在腔内产生的一对光子,每个光子都有50%的概率在腔内损耗或者是耦合到出射波导中,再考虑到出射波导到探测器之间的损耗,接收到一对光子对的概率至多为25%.类似地,在关键耦合时,对于双波导环,每个产生的光子有50%概率在腔内损耗和从第二条波导出射或者50%概率从第一条波导出射,从一条波导收集到两个光子的概率最高为25%.为了解决这一问题,可以利用带有马赫⁃曾德尔干涉仪(Mach–Zehnder Interferometer,MZI)的微环共振腔[59,67].加入输入和输出端的干涉结构后,输入端对于泵浦光为关键耦合,只允许泵浦光进入微环,而不能从任一端耦合出微环,这保证了光子对的产率和高亮度,同时对于产生的信号光子和闲置光子,只允许在输出端被耦出,保证了较高的收集效率.通过改进,可以在获得高产率和亮度的同时获得高的收集效率.不仅如此,由于带有MZI干涉结构的微环可以调节输入(输出)波导和微环之间的耦合系数,从而对微环的Q值进行调制,克服加工因素的影响;此外,因为输出端的干涉结构对泵浦光进行了一次滤波,所以可以减轻腔外滤波的需求. ...
No free lunch:The trade?off between heralding rate and efficiency in microresonator?based heralded single photon sources
1
2016
... 图3b、图3c和图3d展示了产生纠缠光子对实验中用到的作为量子光源的三种微环腔.单波导微环是结构最简单的一种微环共振腔,为了获得最高的光子对产率和亮度,单波导微环需要的耦合类型分别为过耦合和关键耦合[64].由于波导损耗和耦合系数都非常依赖于加工过程,很难做到完全符合预期,而且Qi与Qe非常依赖这两个参数,这会极大地影响集成光源的光子对产率[65].为了消除加工过程对产率的影响,Strain et al[65]在耦合区域增加调制器件,使微环共振腔的Q值可调,从而克服加工中的不确定性.另一方面,也可以采用双波导微环来克服这一问题,这是由于引入第二条波导的耦合,在波导损耗很小的情况下,等效的损耗因子与第一条波导和环之间的耦合系数近似相等,从而达到关键耦合的条件.不过,这些方法虽然增加了光子对的产率和产率的稳定性,但是对于传统的微腔,光子对亮度提高的同时,光子对的预报率(Heralding Efficiency)或收集率会下降[66].对于单波导微环,在关键耦合时获得最高的光子对亮度,此时,对应于损耗因子与耦合系数相等.这意味着,在腔内产生的一对光子,每个光子都有50%的概率在腔内损耗或者是耦合到出射波导中,再考虑到出射波导到探测器之间的损耗,接收到一对光子对的概率至多为25%.类似地,在关键耦合时,对于双波导环,每个产生的光子有50%概率在腔内损耗和从第二条波导出射或者50%概率从第一条波导出射,从一条波导收集到两个光子的概率最高为25%.为了解决这一问题,可以利用带有马赫⁃曾德尔干涉仪(Mach–Zehnder Interferometer,MZI)的微环共振腔[59,67].加入输入和输出端的干涉结构后,输入端对于泵浦光为关键耦合,只允许泵浦光进入微环,而不能从任一端耦合出微环,这保证了光子对的产率和高亮度,同时对于产生的信号光子和闲置光子,只允许在输出端被耦出,保证了较高的收集效率.通过改进,可以在获得高产率和亮度的同时获得高的收集效率.不仅如此,由于带有MZI干涉结构的微环可以调节输入(输出)波导和微环之间的耦合系数,从而对微环的Q值进行调制,克服加工因素的影响;此外,因为输出端的干涉结构对泵浦光进行了一次滤波,所以可以减轻腔外滤波的需求. ...
High?spectral?purity photon generation from a dual?interferometer?coupled silicon microring
1
2020
... 图3b、图3c和图3d展示了产生纠缠光子对实验中用到的作为量子光源的三种微环腔.单波导微环是结构最简单的一种微环共振腔,为了获得最高的光子对产率和亮度,单波导微环需要的耦合类型分别为过耦合和关键耦合[64].由于波导损耗和耦合系数都非常依赖于加工过程,很难做到完全符合预期,而且Qi与Qe非常依赖这两个参数,这会极大地影响集成光源的光子对产率[65].为了消除加工过程对产率的影响,Strain et al[65]在耦合区域增加调制器件,使微环共振腔的Q值可调,从而克服加工中的不确定性.另一方面,也可以采用双波导微环来克服这一问题,这是由于引入第二条波导的耦合,在波导损耗很小的情况下,等效的损耗因子与第一条波导和环之间的耦合系数近似相等,从而达到关键耦合的条件.不过,这些方法虽然增加了光子对的产率和产率的稳定性,但是对于传统的微腔,光子对亮度提高的同时,光子对的预报率(Heralding Efficiency)或收集率会下降[66].对于单波导微环,在关键耦合时获得最高的光子对亮度,此时,对应于损耗因子与耦合系数相等.这意味着,在腔内产生的一对光子,每个光子都有50%的概率在腔内损耗或者是耦合到出射波导中,再考虑到出射波导到探测器之间的损耗,接收到一对光子对的概率至多为25%.类似地,在关键耦合时,对于双波导环,每个产生的光子有50%概率在腔内损耗和从第二条波导出射或者50%概率从第一条波导出射,从一条波导收集到两个光子的概率最高为25%.为了解决这一问题,可以利用带有马赫⁃曾德尔干涉仪(Mach–Zehnder Interferometer,MZI)的微环共振腔[59,67].加入输入和输出端的干涉结构后,输入端对于泵浦光为关键耦合,只允许泵浦光进入微环,而不能从任一端耦合出微环,这保证了光子对的产率和高亮度,同时对于产生的信号光子和闲置光子,只允许在输出端被耦出,保证了较高的收集效率.通过改进,可以在获得高产率和亮度的同时获得高的收集效率.不仅如此,由于带有MZI干涉结构的微环可以调节输入(输出)波导和微环之间的耦合系数,从而对微环的Q值进行调制,克服加工因素的影响;此外,因为输出端的干涉结构对泵浦光进行了一次滤波,所以可以减轻腔外滤波的需求. ...
Generation of path?encoded Greenberger?Horne?Zeilinger states
1
2017
... 而对于简并的SFWM过程,将不同频率的泵浦光耦入芯片后和非简并过程类似,通过分束进入SFWM器件,不同的是由于产生的双光子频率相同,无法通过波分复用器件进行选择分路.如图4b中展示了可以利用产生相同频率的光子对的特点,利用HOM(Hong–Ou–Mandel)干涉,将两量子光源放置在MZI结构的两臂,通过调节两臂相位差使产生的两光子分别进入两条波导[68-69].利用简并方法产生的双光子由于频率相同,分路结构较非简并更为复杂,并且产生效率较非简并方法低,但是由于产生的光子都是同频率的,在多光子高维纠缠线路中具有更大的潜力. ...
Reconfigurable multiphoton entangled states based on quantum photonic chips
1
2020
... 而对于简并的SFWM过程,将不同频率的泵浦光耦入芯片后和非简并过程类似,通过分束进入SFWM器件,不同的是由于产生的双光子频率相同,无法通过波分复用器件进行选择分路.如图4b中展示了可以利用产生相同频率的光子对的特点,利用HOM(Hong–Ou–Mandel)干涉,将两量子光源放置在MZI结构的两臂,通过调节两臂相位差使产生的两光子分别进入两条波导[68-69].利用简并方法产生的双光子由于频率相同,分路结构较非简并更为复杂,并且产生效率较非简并方法低,但是由于产生的光子都是同频率的,在多光子高维纠缠线路中具有更大的潜力. ...
Entanglement by path identity
2
2017
... 近几年,利用路径一致(Path Identity)原理[70]产生量子纠缠的方法也得到关注,Feng et al[71]在芯片上进行了展示.这种原理可以用来实现高维光量子纠缠[72-73],图4c展示了路径一致的块状光学原理图.该原理不仅可以用于双光子高维纠缠态,也同样适用于多光子高维纠缠态.更进一步地,通过构建路径一致实验与图论的联系,可以判断给定纠缠量子态是否可以由线性光学元件结合路径一致原理和后选择得到,并通过图论知识构造性地获得产生给定高维量子态的实验线路[74]. ...
... (3)逐渐向多光子高维量子态发展.多光子高维可以指数倍的增强量子态的总维度,显示出更强的量子优越性[102].然而,片上产生多光子纠缠也面临着挑战,特别是多光子符合项的亮度会随着测量光子数指数衰减,为了解决这一问题,一方面在技术上开发更为低损、高产率的片上量子光源线路;另一方面,在产生纠缠态原理上减少低阶光子项,减少噪声,提高信噪比;近年来提出的路径一致原理[70]显示出利用低阶复合项展示高阶符合的特征[73],也是解决这一问题的可选方法. ...
Observation of nonlocal quantum interference between the origins of a four?photon state in a silicon chip
3
2021
... 近几年,利用路径一致(Path Identity)原理[70]产生量子纠缠的方法也得到关注,Feng et al[71]在芯片上进行了展示.这种原理可以用来实现高维光量子纠缠[72-73],图4c展示了路径一致的块状光学原理图.该原理不仅可以用于双光子高维纠缠态,也同样适用于多光子高维纠缠态.更进一步地,通过构建路径一致实验与图论的联系,可以判断给定纠缠量子态是否可以由线性光学元件结合路径一致原理和后选择得到,并通过图论知识构造性地获得产生给定高维量子态的实验线路[74]. ...
... 2017年Krenn et al[90]发现了图与高维量子纠缠实验一一对应的关系,并由此提出了一种利用高维量子纠缠实验线路对图进行模拟的方法,通过测量与给定图的对应的量子线路产生的量子态的项数,可以得到目标图的完美匹配数,而计算给定图的完美匹配数的算法复杂度是#P完全的[91],2020年,利用三维纠缠光量子态模拟对两个顶点三条边的图已由三维纠缠光量子芯片展示[39].2019年Gu et al[92]扩展了图与量子纠缠实验的对应关系,引入相位和权重.基于这种扩展关系,可以解决更多困难的图论问题,例如对复杂加权图完美匹配权重求和,这也是一个#P完全的问题.2021年Feng et al[71]展示的四光子非区域干涉现象,是这种扩展关系的芯片实现,对应一个四顶点四边图.在此基础上,在芯片上引入更多高维纠缠可以实现更丰富的量子模拟. ...
... 在量子测量和传感领域,可以通过使用纠缠来进一步提高干涉仪和探测设备的灵敏度[3,99].2020年Lu et al[39]利用三维纠缠光量子芯片展示了高维量子纠缠系统出色的相位灵敏度,超过了经典的三路径线性干涉仪和量子二阶非线性干涉仪的极限.2021年,利用Path Identity原理的量子芯片[71]上非区域干涉同样具有相位敏感的特性,结合高维纠缠,可以实现更为灵敏的量子测量和传感器[73].另外,在量子照明原理中[100],维度和纠缠粒子数对灵敏度的增益为,d为纠缠系统的维数,N为纠缠系统粒子数.可以看到,高维纠缠光量子芯片可以在不增加额外光子的情况下实现高集成度和高灵敏度的量子照明雷达光源.随着单光子探测技术的提高,近年来量子照明实验也被报道[101],利用高维纠缠提高增益的演示也有望实现. ...
Path identity as a source of high?dimensional entanglement
1
2020
... 近几年,利用路径一致(Path Identity)原理[70]产生量子纠缠的方法也得到关注,Feng et al[71]在芯片上进行了展示.这种原理可以用来实现高维光量子纠缠[72-73],图4c展示了路径一致的块状光学原理图.该原理不仅可以用于双光子高维纠缠态,也同样适用于多光子高维纠缠态.更进一步地,通过构建路径一致实验与图论的联系,可以判断给定纠缠量子态是否可以由线性光学元件结合路径一致原理和后选择得到,并通过图论知识构造性地获得产生给定高维量子态的实验线路[74]. ...
Quantum Indistinguishability by Path Identity:The awakening of a sleeping beauty
3
2021
... 近几年,利用路径一致(Path Identity)原理[70]产生量子纠缠的方法也得到关注,Feng et al[71]在芯片上进行了展示.这种原理可以用来实现高维光量子纠缠[72-73],图4c展示了路径一致的块状光学原理图.该原理不仅可以用于双光子高维纠缠态,也同样适用于多光子高维纠缠态.更进一步地,通过构建路径一致实验与图论的联系,可以判断给定纠缠量子态是否可以由线性光学元件结合路径一致原理和后选择得到,并通过图论知识构造性地获得产生给定高维量子态的实验线路[74]. ...
... 在量子测量和传感领域,可以通过使用纠缠来进一步提高干涉仪和探测设备的灵敏度[3,99].2020年Lu et al[39]利用三维纠缠光量子芯片展示了高维量子纠缠系统出色的相位灵敏度,超过了经典的三路径线性干涉仪和量子二阶非线性干涉仪的极限.2021年,利用Path Identity原理的量子芯片[71]上非区域干涉同样具有相位敏感的特性,结合高维纠缠,可以实现更为灵敏的量子测量和传感器[73].另外,在量子照明原理中[100],维度和纠缠粒子数对灵敏度的增益为,d为纠缠系统的维数,N为纠缠系统粒子数.可以看到,高维纠缠光量子芯片可以在不增加额外光子的情况下实现高集成度和高灵敏度的量子照明雷达光源.随着单光子探测技术的提高,近年来量子照明实验也被报道[101],利用高维纠缠提高增益的演示也有望实现. ...
... (3)逐渐向多光子高维量子态发展.多光子高维可以指数倍的增强量子态的总维度,显示出更强的量子优越性[102].然而,片上产生多光子纠缠也面临着挑战,特别是多光子符合项的亮度会随着测量光子数指数衰减,为了解决这一问题,一方面在技术上开发更为低损、高产率的片上量子光源线路;另一方面,在产生纠缠态原理上减少低阶光子项,减少噪声,提高信噪比;近年来提出的路径一致原理[70]显示出利用低阶复合项展示高阶符合的特征[73],也是解决这一问题的可选方法. ...
Quantum experiments and graphs
1
2019
... 近几年,利用路径一致(Path Identity)原理[70]产生量子纠缠的方法也得到关注,Feng et al[71]在芯片上进行了展示.这种原理可以用来实现高维光量子纠缠[72-73],图4c展示了路径一致的块状光学原理图.该原理不仅可以用于双光子高维纠缠态,也同样适用于多光子高维纠缠态.更进一步地,通过构建路径一致实验与图论的联系,可以判断给定纠缠量子态是否可以由线性光学元件结合路径一致原理和后选择得到,并通过图论知识构造性地获得产生给定高维量子态的实验线路[74]. ...
Cryogenic operation of silicon photonic modulators based on the DC Kerr effect
1
2020
... 图5显示了片上路径编码光量子态的基本操控单元.由相移器和一个MZI结构组成一个二维通用局域线性操作,可以实现任意的SU(2)操作.对两部分的相移器进行控制,对应于旋转块状光学实验中的四分之一玻片和二分之一玻片的角度.相移器主要根据电光原理和热光原理进行相位的控制.通过电光相移器可以获得很高的调制速率[75-76],是未来片上光学调制的发展趋势,但目前部分高速调制依赖于较为苛刻的实验条件[77],并且可能会引起较大的损耗.目前对于产生片上高维纠缠光量子,基于热光相移器的速率已经可以满足基本要求,并且热光调制较为成熟,在近年来的片上高维纠缠光量子实验[21,38-39]中,使用的都是基于热光效应的热光相移器.热光相移器通过由大阻值导电材料(如氮化钛)构成的加热层通电,使加热层发热,引起周围波导温度升高,由于波导材料的折射率随温度变化,导致波导等效折射率的改变,从而引起光子相位的改变. ...
Ultralow drive voltage silicon traveling?wave modulator
1
2012
... 图5显示了片上路径编码光量子态的基本操控单元.由相移器和一个MZI结构组成一个二维通用局域线性操作,可以实现任意的SU(2)操作.对两部分的相移器进行控制,对应于旋转块状光学实验中的四分之一玻片和二分之一玻片的角度.相移器主要根据电光原理和热光原理进行相位的控制.通过电光相移器可以获得很高的调制速率[75-76],是未来片上光学调制的发展趋势,但目前部分高速调制依赖于较为苛刻的实验条件[77],并且可能会引起较大的损耗.目前对于产生片上高维纠缠光量子,基于热光相移器的速率已经可以满足基本要求,并且热光调制较为成熟,在近年来的片上高维纠缠光量子实验[21,38-39]中,使用的都是基于热光效应的热光相移器.热光相移器通过由大阻值导电材料(如氮化钛)构成的加热层通电,使加热层发热,引起周围波导温度升高,由于波导材料的折射率随温度变化,导致波导等效折射率的改变,从而引起光子相位的改变. ...
Operation of high?speed silicon photonic micro?disk modulators at cryogenic temperatures
1
2017
... 图5显示了片上路径编码光量子态的基本操控单元.由相移器和一个MZI结构组成一个二维通用局域线性操作,可以实现任意的SU(2)操作.对两部分的相移器进行控制,对应于旋转块状光学实验中的四分之一玻片和二分之一玻片的角度.相移器主要根据电光原理和热光原理进行相位的控制.通过电光相移器可以获得很高的调制速率[75-76],是未来片上光学调制的发展趋势,但目前部分高速调制依赖于较为苛刻的实验条件[77],并且可能会引起较大的损耗.目前对于产生片上高维纠缠光量子,基于热光相移器的速率已经可以满足基本要求,并且热光调制较为成熟,在近年来的片上高维纠缠光量子实验[21,38-39]中,使用的都是基于热光效应的热光相移器.热光相移器通过由大阻值导电材料(如氮化钛)构成的加热层通电,使加热层发热,引起周围波导温度升高,由于波导材料的折射率随温度变化,导致波导等效折射率的改变,从而引起光子相位的改变. ...
Optical multi?mode interference devices based on self?imaging:Principles and applications
1
1995
... 片上MZI结构(图5b和图5d)由两个1∶1分束器和一个相移器组成.定向耦合器(Directional Coupler,DC)和多模干涉器(Multi⁃Mode Interferometer,MMI,图5c)是两种常用的分束器件,和DC比较,MMI具有加工误差容忍度高、对波长和温度敏感性低的特点[78],是目前MZI结构中分束器的首选器件. ...
Experimental realization of any discrete unitary operator
1
1994
... 实现通用操控线路需要利用可以实现酉矩阵操作的线路.图6为两种主要的片上酉矩阵操作线路的示意图.图6a展示的线路是通过将SU(N)的变换分解为一系列SU(2)的变换来实现的,而任意的SU(2)操作可以被基本操控单元实现,这在块状光学实验中已有报道[79-80],并对使用的干涉器件数量进行了优化[81].Schaeff et al[82]实现了基于此方法的集成三维模块.图6b展示了经典光学芯片研究[83-84]中基于级联相移器和模式耦合器的线路实现方式.在高维光量子态调控中,这种线路实现方法已应用在频率编码中,电光相移器则起到了模式耦合器的作用[25];在路径编码中,模式耦合器可以采用MMI或者DC来实现. ...
Realizable higher?dimensional two?particle entanglements via multiport beam splitters
1
1997
... 实现通用操控线路需要利用可以实现酉矩阵操作的线路.图6为两种主要的片上酉矩阵操作线路的示意图.图6a展示的线路是通过将SU(N)的变换分解为一系列SU(2)的变换来实现的,而任意的SU(2)操作可以被基本操控单元实现,这在块状光学实验中已有报道[79-80],并对使用的干涉器件数量进行了优化[81].Schaeff et al[82]实现了基于此方法的集成三维模块.图6b展示了经典光学芯片研究[83-84]中基于级联相移器和模式耦合器的线路实现方式.在高维光量子态调控中,这种线路实现方法已应用在频率编码中,电光相移器则起到了模式耦合器的作用[25];在路径编码中,模式耦合器可以采用MMI或者DC来实现. ...
Optimal design for universal multiport inter?ferometers
1
2016
... 实现通用操控线路需要利用可以实现酉矩阵操作的线路.图6为两种主要的片上酉矩阵操作线路的示意图.图6a展示的线路是通过将SU(N)的变换分解为一系列SU(2)的变换来实现的,而任意的SU(2)操作可以被基本操控单元实现,这在块状光学实验中已有报道[79-80],并对使用的干涉器件数量进行了优化[81].Schaeff et al[82]实现了基于此方法的集成三维模块.图6b展示了经典光学芯片研究[83-84]中基于级联相移器和模式耦合器的线路实现方式.在高维光量子态调控中,这种线路实现方法已应用在频率编码中,电光相移器则起到了模式耦合器的作用[25];在路径编码中,模式耦合器可以采用MMI或者DC来实现. ...
Experimental access to higher?dimensional entangled quantum systems using integrated optics
1
2015
... 实现通用操控线路需要利用可以实现酉矩阵操作的线路.图6为两种主要的片上酉矩阵操作线路的示意图.图6a展示的线路是通过将SU(N)的变换分解为一系列SU(2)的变换来实现的,而任意的SU(2)操作可以被基本操控单元实现,这在块状光学实验中已有报道[79-80],并对使用的干涉器件数量进行了优化[81].Schaeff et al[82]实现了基于此方法的集成三维模块.图6b展示了经典光学芯片研究[83-84]中基于级联相移器和模式耦合器的线路实现方式.在高维光量子态调控中,这种线路实现方法已应用在频率编码中,电光相移器则起到了模式耦合器的作用[25];在路径编码中,模式耦合器可以采用MMI或者DC来实现. ...
Integrated reconfigurable unitary optical mode converter using MMI couplers
1
2017
... 实现通用操控线路需要利用可以实现酉矩阵操作的线路.图6为两种主要的片上酉矩阵操作线路的示意图.图6a展示的线路是通过将SU(N)的变换分解为一系列SU(2)的变换来实现的,而任意的SU(2)操作可以被基本操控单元实现,这在块状光学实验中已有报道[79-80],并对使用的干涉器件数量进行了优化[81].Schaeff et al[82]实现了基于此方法的集成三维模块.图6b展示了经典光学芯片研究[83-84]中基于级联相移器和模式耦合器的线路实现方式.在高维光量子态调控中,这种线路实现方法已应用在频率编码中,电光相移器则起到了模式耦合器的作用[25];在路径编码中,模式耦合器可以采用MMI或者DC来实现. ...
Photonic matrix computing:From fundamentals to applications
1
2021
... 实现通用操控线路需要利用可以实现酉矩阵操作的线路.图6为两种主要的片上酉矩阵操作线路的示意图.图6a展示的线路是通过将SU(N)的变换分解为一系列SU(2)的变换来实现的,而任意的SU(2)操作可以被基本操控单元实现,这在块状光学实验中已有报道[79-80],并对使用的干涉器件数量进行了优化[81].Schaeff et al[82]实现了基于此方法的集成三维模块.图6b展示了经典光学芯片研究[83-84]中基于级联相移器和模式耦合器的线路实现方式.在高维光量子态调控中,这种线路实现方法已应用在频率编码中,电光相移器则起到了模式耦合器的作用[25];在路径编码中,模式耦合器可以采用MMI或者DC来实现. ...
Photonic state tomography
1
2005
... 通用操控线路的功能也可大致分为两类:一类是实现任意的单光子局域酉操作,实现SU(N)的变换;另一类是结合后选择实现任意的双光子及多光子门操作.第一类可以对产生的双光子态进行任意的局域酉变换,并通过局域变换对产生的量子态进行量子态断层扫描(Quantum Tomography)[85].在集成三维和十五维光量子芯片实验[38-39]中使用类似的方法来完成高维纠缠光量子的操控和分析,并且采用基于SU(2)单元的酉矩阵线路.实现N维通用局域酉操作一般需要个基本操作单元.随着操作单元的增加,一方面使得操作模块的尺寸增大,另一方面控制的电路和热调器件的复杂度也在增加,电热管理的难度增加.在操控15维的纠缠光子态时[38],采用了只保留信号光子和闲置光子输出部分各一个输出口的方法进行线路简化,相当于从原先的测量一个完整的光子态状态向量,变为每次测量状态向量中的一个元素,这样使芯片上的操作模块的数量降低,需要探测次数相应增加.第二类结合后选择,可以概率性地实现通用双光子量子门(任意双光子酉变换).Qiang et al[21]利用四个酉矩阵的线性组合实现了两光子四维量子门,展示了98个不同的双光子四维量子门,平均操作保真度超过93%.使用的每个四维酉矩阵都由基本操控单元构成,结构简单.使用这类线路可以实现的量子操作大大增加了,与之相对应地,调制器的数量也明显增加.高保真度的多光子高维的通用操作线路也可以实现[86]. ...
Universal linear optics
1
2015
... 通用操控线路的功能也可大致分为两类:一类是实现任意的单光子局域酉操作,实现SU(N)的变换;另一类是结合后选择实现任意的双光子及多光子门操作.第一类可以对产生的双光子态进行任意的局域酉变换,并通过局域变换对产生的量子态进行量子态断层扫描(Quantum Tomography)[85].在集成三维和十五维光量子芯片实验[38-39]中使用类似的方法来完成高维纠缠光量子的操控和分析,并且采用基于SU(2)单元的酉矩阵线路.实现N维通用局域酉操作一般需要个基本操作单元.随着操作单元的增加,一方面使得操作模块的尺寸增大,另一方面控制的电路和热调器件的复杂度也在增加,电热管理的难度增加.在操控15维的纠缠光子态时[38],采用了只保留信号光子和闲置光子输出部分各一个输出口的方法进行线路简化,相当于从原先的测量一个完整的光子态状态向量,变为每次测量状态向量中的一个元素,这样使芯片上的操作模块的数量降低,需要探测次数相应增加.第二类结合后选择,可以概率性地实现通用双光子量子门(任意双光子酉变换).Qiang et al[21]利用四个酉矩阵的线性组合实现了两光子四维量子门,展示了98个不同的双光子四维量子门,平均操作保真度超过93%.使用的每个四维酉矩阵都由基本操控单元构成,结构简单.使用这类线路可以实现的量子操作大大增加了,与之相对应地,调制器的数量也明显增加.高保真度的多光子高维的通用操作线路也可以实现[86]. ...
Efficient,compact and low loss thermo?optic phase shifter in silicon
1
2014
... 高维纠缠光量子芯片上不可避免地具有较多的调制器件,由于目前相移器主要采用热调控器件,每个热调控器件大约需要消耗微瓦量级的功率,这使芯片上的热管理成为一个必须要面对的问题.热管理对采用了微环共振腔作为光子对源的芯片十分关键[39],因为共振结构对温度十分敏感,各个微环受热不相等时,会使不同微环中共振峰出现不同程度的平移,导致光源的不可分辨性被破坏,造成量子态的纯度降低.除了2.1和2.2中提到的设计方法可以降低器件的热敏感度以及减小热调制器件的数量外,也可以通过设计调制器件的方法来克服热串扰.Harris et al[87]设计了不同掺杂浓度的电阻截面使电流传输垂直于波导获得局域性发热和减小热串扰.Gao et al[88]通过独立的条形波导并部分挖空衬底的方式实现了具有高效但显著热隔离的调制.Jacques et al[89]采用热调器件之间进行刻蚀和结构优化的方法减小调制器之间的热串扰. ...
Power?efficient thermal optical tunable grating coupler based on silicon photonic platform
1
2019
... 高维纠缠光量子芯片上不可避免地具有较多的调制器件,由于目前相移器主要采用热调控器件,每个热调控器件大约需要消耗微瓦量级的功率,这使芯片上的热管理成为一个必须要面对的问题.热管理对采用了微环共振腔作为光子对源的芯片十分关键[39],因为共振结构对温度十分敏感,各个微环受热不相等时,会使不同微环中共振峰出现不同程度的平移,导致光源的不可分辨性被破坏,造成量子态的纯度降低.除了2.1和2.2中提到的设计方法可以降低器件的热敏感度以及减小热调制器件的数量外,也可以通过设计调制器件的方法来克服热串扰.Harris et al[87]设计了不同掺杂浓度的电阻截面使电流传输垂直于波导获得局域性发热和减小热串扰.Gao et al[88]通过独立的条形波导并部分挖空衬底的方式实现了具有高效但显著热隔离的调制.Jacques et al[89]采用热调器件之间进行刻蚀和结构优化的方法减小调制器之间的热串扰. ...
Optimization of thermo?optic phase?shifter design and mitigation of thermal crosstalk on the SOI platform
1
2019
... 高维纠缠光量子芯片上不可避免地具有较多的调制器件,由于目前相移器主要采用热调控器件,每个热调控器件大约需要消耗微瓦量级的功率,这使芯片上的热管理成为一个必须要面对的问题.热管理对采用了微环共振腔作为光子对源的芯片十分关键[39],因为共振结构对温度十分敏感,各个微环受热不相等时,会使不同微环中共振峰出现不同程度的平移,导致光源的不可分辨性被破坏,造成量子态的纯度降低.除了2.1和2.2中提到的设计方法可以降低器件的热敏感度以及减小热调制器件的数量外,也可以通过设计调制器件的方法来克服热串扰.Harris et al[87]设计了不同掺杂浓度的电阻截面使电流传输垂直于波导获得局域性发热和减小热串扰.Gao et al[88]通过独立的条形波导并部分挖空衬底的方式实现了具有高效但显著热隔离的调制.Jacques et al[89]采用热调器件之间进行刻蚀和结构优化的方法减小调制器之间的热串扰. ...
Quantum experiments and graphs:Multiparty states as coherent superpositions of perfect matchings
1
2017
... 2017年Krenn et al[90]发现了图与高维量子纠缠实验一一对应的关系,并由此提出了一种利用高维量子纠缠实验线路对图进行模拟的方法,通过测量与给定图的对应的量子线路产生的量子态的项数,可以得到目标图的完美匹配数,而计算给定图的完美匹配数的算法复杂度是#P完全的[91],2020年,利用三维纠缠光量子态模拟对两个顶点三条边的图已由三维纠缠光量子芯片展示[39].2019年Gu et al[92]扩展了图与量子纠缠实验的对应关系,引入相位和权重.基于这种扩展关系,可以解决更多困难的图论问题,例如对复杂加权图完美匹配权重求和,这也是一个#P完全的问题.2021年Feng et al[71]展示的四光子非区域干涉现象,是这种扩展关系的芯片实现,对应一个四顶点四边图.在此基础上,在芯片上引入更多高维纠缠可以实现更丰富的量子模拟. ...
The complexity of computing the permanent
1
1979
... 2017年Krenn et al[90]发现了图与高维量子纠缠实验一一对应的关系,并由此提出了一种利用高维量子纠缠实验线路对图进行模拟的方法,通过测量与给定图的对应的量子线路产生的量子态的项数,可以得到目标图的完美匹配数,而计算给定图的完美匹配数的算法复杂度是#P完全的[91],2020年,利用三维纠缠光量子态模拟对两个顶点三条边的图已由三维纠缠光量子芯片展示[39].2019年Gu et al[92]扩展了图与量子纠缠实验的对应关系,引入相位和权重.基于这种扩展关系,可以解决更多困难的图论问题,例如对复杂加权图完美匹配权重求和,这也是一个#P完全的问题.2021年Feng et al[71]展示的四光子非区域干涉现象,是这种扩展关系的芯片实现,对应一个四顶点四边图.在此基础上,在芯片上引入更多高维纠缠可以实现更丰富的量子模拟. ...
Quantum experiments and graphs Ⅱ:Quantum interference,computation,and state generation
1
2019
... 2017年Krenn et al[90]发现了图与高维量子纠缠实验一一对应的关系,并由此提出了一种利用高维量子纠缠实验线路对图进行模拟的方法,通过测量与给定图的对应的量子线路产生的量子态的项数,可以得到目标图的完美匹配数,而计算给定图的完美匹配数的算法复杂度是#P完全的[91],2020年,利用三维纠缠光量子态模拟对两个顶点三条边的图已由三维纠缠光量子芯片展示[39].2019年Gu et al[92]扩展了图与量子纠缠实验的对应关系,引入相位和权重.基于这种扩展关系,可以解决更多困难的图论问题,例如对复杂加权图完美匹配权重求和,这也是一个#P完全的问题.2021年Feng et al[71]展示的四光子非区域干涉现象,是这种扩展关系的芯片实现,对应一个四顶点四边图.在此基础上,在芯片上引入更多高维纠缠可以实现更丰富的量子模拟. ...
Implementing graph?theoretic quantum algorithms on a silicon photonic quantum walk processor
1
2021
... 2018年Qiang et al[21]利用四维纠缠光量子芯片演示了量子近似优化算法(Quantum Approximate Optimization algorithm,QAOA),QAOA可以用来寻找组合搜索问题的近似解,实验中用以解决其中的三个示例约束满足问题(Three Example Constraint Satisfaction Problems,CSPs).同时以在两节点加权图为例,也进行了一类量子游走,即Szegedy量子游走的模拟.2021年,在硅芯片上利用纠缠特性,实现了在任意五顶点图上的纠缠双光子的量子游走[93],展示了对图搜索问题的经典二次加速算法和在多项式时间内判断图同构的量子游走算法. ...
An entanglement?based quantum network based on symmetric dispersive optics quantum key distribution
1
2020
... 高维纠缠可以在量子通信网络中发挥巨大作用.2018年Wengerowsky et al [54]利用块状光学产生的高维频率纠缠结合波分复用器件来建立多用户之间的量子秘钥分发网络.2020年,该方案用于改进用户之间的连接方式,Liu et al[94]和Joshi et al[95]将其进一步优化和扩展,用户数量显著提升.2021年,也报道了利用片上产生的纠缠光源实现的量子通信网络[96]. ...
A trusted node–free eight?user metropolitan quantum communication network
1
2020
... 高维纠缠可以在量子通信网络中发挥巨大作用.2018年Wengerowsky et al [54]利用块状光学产生的高维频率纠缠结合波分复用器件来建立多用户之间的量子秘钥分发网络.2020年,该方案用于改进用户之间的连接方式,Liu et al[94]和Joshi et al[95]将其进一步优化和扩展,用户数量显著提升.2021年,也报道了利用片上产生的纠缠光源实现的量子通信网络[96]. ...
Flexible entanglement?distribution network with an AlGaAs chip for secure communications
1
2021
... 高维纠缠可以在量子通信网络中发挥巨大作用.2018年Wengerowsky et al [54]利用块状光学产生的高维频率纠缠结合波分复用器件来建立多用户之间的量子秘钥分发网络.2020年,该方案用于改进用户之间的连接方式,Liu et al[94]和Joshi et al[95]将其进一步优化和扩展,用户数量显著提升.2021年,也报道了利用片上产生的纠缠光源实现的量子通信网络[96]. ...
Path?encoded high?dimensional quantum communication over a 2 km multicore fiber
1
2021
... 另一方面,在多用户之间建立高维纠缠也是实现多用户之间的量子通信的一种方案[19].同时高维纠缠在量子密钥分发中也可以起到抵御噪声[97]和增强容错率的作用[98],利用集成技术进行高维纠缠产生和调制的芯片也是直接的,可以预见这些量子通信方案的集成化. ...
Quantum key distribution overcoming extreme noise:Simultaneous subspace coding using high?dimensional entanglement
1
2021
... 另一方面,在多用户之间建立高维纠缠也是实现多用户之间的量子通信的一种方案[19].同时高维纠缠在量子密钥分发中也可以起到抵御噪声[97]和增强容错率的作用[98],利用集成技术进行高维纠缠产生和调制的芯片也是直接的,可以预见这些量子通信方案的集成化. ...
Advances in photonic quantum sensing
1
2018
... 在量子测量和传感领域,可以通过使用纠缠来进一步提高干涉仪和探测设备的灵敏度[3,99].2020年Lu et al[39]利用三维纠缠光量子芯片展示了高维量子纠缠系统出色的相位灵敏度,超过了经典的三路径线性干涉仪和量子二阶非线性干涉仪的极限.2021年,利用Path Identity原理的量子芯片[71]上非区域干涉同样具有相位敏感的特性,结合高维纠缠,可以实现更为灵敏的量子测量和传感器[73].另外,在量子照明原理中[100],维度和纠缠粒子数对灵敏度的增益为,d为纠缠系统的维数,N为纠缠系统粒子数.可以看到,高维纠缠光量子芯片可以在不增加额外光子的情况下实现高集成度和高灵敏度的量子照明雷达光源.随着单光子探测技术的提高,近年来量子照明实验也被报道[101],利用高维纠缠提高增益的演示也有望实现. ...
Enhanced sensitivity of photodetection via quantum illumination
1
2008
... 在量子测量和传感领域,可以通过使用纠缠来进一步提高干涉仪和探测设备的灵敏度[3,99].2020年Lu et al[39]利用三维纠缠光量子芯片展示了高维量子纠缠系统出色的相位灵敏度,超过了经典的三路径线性干涉仪和量子二阶非线性干涉仪的极限.2021年,利用Path Identity原理的量子芯片[71]上非区域干涉同样具有相位敏感的特性,结合高维纠缠,可以实现更为灵敏的量子测量和传感器[73].另外,在量子照明原理中[100],维度和纠缠粒子数对灵敏度的增益为,d为纠缠系统的维数,N为纠缠系统粒子数.可以看到,高维纠缠光量子芯片可以在不增加额外光子的情况下实现高集成度和高灵敏度的量子照明雷达光源.随着单光子探测技术的提高,近年来量子照明实验也被报道[101],利用高维纠缠提高增益的演示也有望实现. ...
Imaging through noise with quantum illumination
1
2020
... 在量子测量和传感领域,可以通过使用纠缠来进一步提高干涉仪和探测设备的灵敏度[3,99].2020年Lu et al[39]利用三维纠缠光量子芯片展示了高维量子纠缠系统出色的相位灵敏度,超过了经典的三路径线性干涉仪和量子二阶非线性干涉仪的极限.2021年,利用Path Identity原理的量子芯片[71]上非区域干涉同样具有相位敏感的特性,结合高维纠缠,可以实现更为灵敏的量子测量和传感器[73].另外,在量子照明原理中[100],维度和纠缠粒子数对灵敏度的增益为,d为纠缠系统的维数,N为纠缠系统粒子数.可以看到,高维纠缠光量子芯片可以在不增加额外光子的情况下实现高集成度和高灵敏度的量子照明雷达光源.随着单光子探测技术的提高,近年来量子照明实验也被报道[101],利用高维纠缠提高增益的演示也有望实现. ...
Error protected qubits in a silicon photonic chip
1
2020
... (3)逐渐向多光子高维量子态发展.多光子高维可以指数倍的增强量子态的总维度,显示出更强的量子优越性[102].然而,片上产生多光子纠缠也面临着挑战,特别是多光子符合项的亮度会随着测量光子数指数衰减,为了解决这一问题,一方面在技术上开发更为低损、高产率的片上量子光源线路;另一方面,在产生纠缠态原理上减少低阶光子项,减少噪声,提高信噪比;近年来提出的路径一致原理[70]显示出利用低阶复合项展示高阶符合的特征[73],也是解决这一问题的可选方法. ...
On?chip coherent conversion of photonic quantum entanglement between different degrees of freedom
1
2016
... (5)目前,具有片上产生和操控高维量子纠缠态的光学芯片主要基于路径编码.近几年,基于片上各种编码的技术都在迅速发展,多自由度的编码形式会成为高维纠缠光量子芯片强有力的工具.同时,各自由度之间的片上转换[103]也为各编码形式的发展和结合铺垫了道路. ...