基于三元因子分析的三元概念约简

doi:10.13232/j.cnki.jnju.2020.04.006

基于三元因子分析的三元概念约简

李俊余¹^,², 李星璇¹, 王霞^,¹^,², 吴伟志¹^,²

1.浙江海洋大学数理与信息学院，舟山，316022

2.浙江省海洋大数据挖掘与应用重点实验室，浙江海洋大学，舟山，316022

Reduction of triadic concepts based on triadic factor analysis

Li Junyu¹^,², Li Xingxuan¹, Wang Xia^,¹^,², Wu Weizhi¹^,²

1.School of Mathematics，Physics and Information Science，Zhejiang Ocean University，Zhoushan，316022，China

2.Key Laboratory of Oceanographic Big Data Mining and Application of Zhejiang Province，Zhejiang Ocean University，Zhoushan，316022，China

通讯作者: E⁃mail：bblylm@126.com

收稿日期: 2020-06-20 网络出版日期: 2020-08-05

基金资助:

国家自然科学基金. 41631179. 61773349. 61976194
浙江省自然科学基金. LY18F030017

Received: 2020-06-20 Online: 2020-08-05

摘要

三元概念的约简是三元概念分析的重要问题，因为它既能简化三元图的表示，又有助于更好地理解三元概念的语意并从中提取有价值的信息.基于三元因子分析,研究保持三元背景中所有三元关系不变的三元概念约简.首先，基于三元因子分析提出三元概念约简的定义.该方法是在保持三元背景不变的条件下寻找尽可能少的三元概念，即这些三元概念能够完整地反映原始三元背景所包含的所有三元关系.其次，讨论三元因子分解与三元概念协调集的关系，并给出三元概念协调集和约简的判定方法.最后，利用三元概念约简将三元概念分为三类：核心（绝对必要）概念、相对必要概念和不必要概念，并得到每类三元概念的充要条件.此外，通过实例给出由三元因子分解和概念约简定义两种方法寻找三元概念约简的详细过程.

关键词： 形式概念分析 ; 三元背景 ; 三元概念 ; 三元概念约简

Abstract

The reduction of triadic concepts is an important problem in triadic concept analysis，because it can not only simplify the representation of triadic graphs，but also help to better understand the meaning of triadic concepts and extract valuable information from them. Based on the triadic factor analysis，reduction of triadic concepts is studied to keep all the triadic relationships in the triadic context. Firstly，a reduction of triadic concept is defined based on triadic factor analysis. The method is to find as few triadic concepts as possible under the condition of preserving the original triadic context. That is these selected triadic concepts can completely reflect all the triadic relations contained in the original triadic context. Secondly，the relationship between the triadic factorizations and the triadic concept consistent sets is discussed，and the necessary and sufficient conditions for consistent sets and reducts are given. Finally，the triadic concepts are classified into three categories by using triadic concept reduction: core （absolute necessary） concept，relative necessary concept and unnecessary concept. Moreover，the necessary and sufficient conditions for each class of triadic concepts are obtained. In addition，the detailed process of finding triadic concept reduct using triadic factorization and the definition of reduction is given by an example.

Keywords： formal concept analysis ; triadic context ; triadic concept ; triadic concept reduction

PDF (1085KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李俊余, 李星璇, 王霞, 吴伟志. 基于三元因子分析的三元概念约简. 南京大学学报（自然科学）[J], 2020, 56(4): 480-493 doi:10.13232/j.cnki.jnju.2020.04.006

Li Junyu, Li Xingxuan, Wang Xia, Wu Weizhi. Reduction of triadic concepts based on triadic factor analysis. Journal of nanjing University[J], 2020, 56(4): 480-493 doi:10.13232/j.cnki.jnju.2020.04.006

1995年,Lehmann and Wille^[1]提出形式概念的三维方法，即三元概念分析，它的研究对象是由对象集、属性集、条件集和三元关系构成的三元背景.三元概念分析的另一个基本概念是由外延、内涵和方式构成的一个三元组，即三元概念.三元概念分析从形式上来看类似形式概念分析^[2-3]，但是有关三元概念分析的研究与发展远不如形式概念分析.当三元背景中数据量比较大时，三元概念可能也会随之变得很多，那么三元概念的三元图表示以及三元概念的语意解释也会变得更加繁琐，这在一定程度上制约了三元概念分析的理论研究和应用.因此，为了能更好地理解三元概念的涵义并从中提取有价值的信息，有必要对三元概念做适当的约简.

目前，形式概念分析与布尔因子分析相结合^[4-6]、三元形式概念分析与布尔因子分析相结合^[7-11]均取得了一些很好的研究成果.因子分析最早是由英国心理学家斯皮尔曼提出的，它的基本目的是用少数几个因子或类别线性地描述许多指标或因素之间的联系，这几个因子或类别能够反映原始因素之间的主要信息.布尔因子分析主要是针对布尔数据的一种因子分析方法，它的主要目的是寻找 $m$ 个因子来表示原始的 $p$ 个变量，要求 $m$ 远远小于 $p$ .

曹丽等^[12]基于布尔因子分析提出了保持二元关系不变的概念约简，该方法在保持形式背景的二元关系不变的前提下对形式概念进行约简.受此启发，本文考虑利用三元因子分析来研究三元概念的约简问题.首先，定义基于三元因子分析的三元概念约简的概念，给出三元因子分解和三元概念协调集的关系，并通过实例给出利用因子分解法和定义法寻找三元概念约简的过程.最后给出三元概念协调集的判断方法，并对三元概念进行分类，给出每类三元概念的判定方法.

1 相关工作

本节给出形式概念分析和三元概念分析的基本概念和结论.

1.1　形式概念分析相关知识

定义1^[2] 称 $(G, M, I)$ 为形式背景，其中 $G$ 是一个对象集， $M$ 是一个属性集， $I$ 是 $G$ 和 $M$ 之间的一个关系.分别称 $G$ 和 $M$ 的元素为对象和属性.

若对象g和属性m具有关系 $I$ ，则记为 $g I m$ .

定义2^[2] 设 $(G, M, I)$ 为形式背景， $X \subseteq G$ ， $B \subseteq M$ ，若二元组 $(X, B)$ 满足 $X' = B$ ， $B' = X$ ，则称 $(X, B)$ 为形式概念，其中,

X' = \{m \in M| \forall g \in X, g I m\}

(1)

B' = \{g \in G| \forall m \in B, g I m\}

(2)

设 $(G, M, I)$ 是形式背景，对任意的形式概念 $(X_{1}, B_{1}), (X_{2}, B_{2})$ 定义如下偏序关系：

(X_{1}, B_{1}) \leq (X_{2}, B_{2}) \Leftrightarrow X_{1} \subseteq X_{2} (\Leftrightarrow B_{1} \supseteq B_{2})

也称 $(X_{1}, B_{1})$ 为子概念， $(X_{2}, B_{2})$ 为父概念.

记 $L (G, M, I)$ 表示形式背景 $(G, M, I)$ 中所有形式概念构成的集合.容易证明 $L (G, M, I)$ 是格,称其为形式背景 $(G, M, I)$ 的概念格.在概念格 $L (G, M, I)$ 上定义上、下确界如下：

(X_{1}, B_{1}) \land (X_{2}, B_{2}) = (X_{1} ⋂ X_{2}, {(B_{1} ⋃ B_{2})}^{})

(3)

(X_{1}, B_{1}) \lor (X_{2}, B_{2}) = ({(X_{1} ⋃ X_{2})}^{}, B_{1} ⋂ B_{2})

(4)

则概念格 $L (G, M, I)$ 是一个完备格.

性质1^[2] 设 $(G, M, I)$ 为形式背景， $X, X_{1}, X_{2}$ 为任意的对象子集, $B, B_{1}, B_{2}$ 为任意的属性子集，则有下列几条性质成立：

(1)若 $X_{1} \subseteq X_{2}$ ，则 ${X_{2}}^{'} \subseteq {X_{1}}^{'}$ ；若 $B_{1} \subseteq B_{2}$ ，则 ${B_{2}}^{'} \subseteq {B_{1}}^{'}$ .

(2) $X \subseteq X ″$ , $B \subseteq B ″$ .

(3) $X' = X ‴$ , $B' = B ‴$ .

(4) ${(X_{1} ⋂ X_{2})}^{'} \supseteq X_{1}^{'} ⋃ X_{2}^{'},$

{(B_{1} ⋂ B_{2})}^{'} \supseteq B_{1}^{'} ⋃ B_{2}^{'}

(5) ${(X_{1} ⋃ X_{2})}^{'} = X_{1}^{'} ⋂ X_{2}^{'},$

{(B_{1} ⋃ B_{2})}^{'} = B_{1}^{'} ⋂ B_{2}^{'}

(6) $(X ″, X') \in L (G, M, I)$ .

(7) $X \subseteq B' \Leftrightarrow B \subseteq X'$ .

1.2　三元概念分析相关知识

在过去几年里，类似Bibsonomy的三维数据（用户、标签、资源）的数据挖掘吸引了从事社交网站服务人员的注意.此类型的数据对数据的处理能力提出了更高的要求，形式概念分析已无法高效地处理这类数据.三元概念分析是在形式背景中引入对象和属性的条件语义后扩展而成，它针对三维数据表进行数据分析，从中提炼出有意义的、简洁的知识.三元概念分析不但具有形式概念分析的方法和技巧，而且有其自身的独特性.

定义3^[1] 称 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，其中 $K_{1}, K_{2}, K_{3}$ 为非空集合，Y为 $K_{1}, K_{2}, K_{3}$ 之间的关系，即 $Y \subseteq K_{1} \times K_{2} \times K_{3}$ .分别称 $K_{1}, K_{2},$

$K_{3}$ 为对象集、属性集和条件集.分别称 $K_{1}, K_{2}, K_{3}$ 的元素为对象、属性和条件.

若对象g、属性 $m$ 和条件 $b$ 具有关系Y，则记为 $(g, m, b) \in Y$ ，表示对象g在条件 $b$ 下具有属性 $m$ .

设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $\{i, j, k\} =$

$\{1,2, 3\}$ ，且 $j < k, X \subseteq K_{i}, Z \subseteq K_{j} \times K_{k}$ ，Lehmann and Wille^[1]定义了(i)⁃诱导算子：

\begin{array}{l} X^{(i)} = \{(a_{j}, a_{k}) \in K_{j} \times K_{k}| \forall a_{i} \in K_{i}, \\ a_{i}, a_{j}, a_{k} 具 有 关 系 Y\} \end{array}

(5)

Z^{(i)} = \{a_{i} \in K_{i}| \forall (a_{j}, a_{k}) \in Z, a_{i}, a_{j}, a_{k} 具 有 关 系 Y\}

(6)

(i)⁃诱导算子相当于形式背景 $K^{(i)} = (K_{i}, K_{j} \times K_{k}, Y^{(i)})$ 上的 $'$ 算子，其中 $\forall a_{i} \in K_{i}$ ， $a_{j} \in K_{j}$ , $a_{k} \in K_{k}$ ，有 $a_{i} Y^{(i)} (a_{j}, a_{k})$ 等价于 $a_{i}, a_{j}, a_{k}$ 具有关系Y.

\forall X_{i} \subseteq K_{i}

，

X_{j} \subseteq K_{j}

，

A_{k} \subseteq K_{k}

，定义

(i, j, A_{k})

⁃

诱导算子如下：

\begin{array}{l} {X_{i}}^{(i, j, A_{k})} = \{a_{j} \in K_{j}| \forall (a_{i}, a_{k}) \in X_{i} \times A_{k}, \\ a_{i}, a_{j}, a_{k} 具 有 关 系 Y\} \end{array}

(7)

\begin{array}{l} {X_{j}}^{(i, j, A_{k})} = \{a_{i} \in K_{i}| \forall (a_{j}, a_{k}) \in X_{j} \times A_{k}, \\ a_{i}, a_{j}, a_{k} 具 有 关 系 Y\} \end{array}

(8)

$(i, j, A_{k})$ ⁃诱导算子相当于形式背景 $K_{A_{k}}^{i j} = (K_{i}, K_{j}, Y_{A_{k}}^{i j})$ 上的 $'$ 算子，其中 $(a_{i}, a_{j}) \in Y_{A_{k}}^{i j}$ 等价于 $\forall a_{k} \in A_{k}$ ， $a_{i}, a_{j}, a_{k} 具有关系 Y$ .

定义4^[1] 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，称 $(A_{1}, A_{2}, A_{3})$ 为三元背景K的一个三元概念.如果对 $\{i, j, k\} = \{1,2, 3\}$ ， $j < k$ ,且 $A_{i} \subseteq K_{i}$ 有 $A_{i} = (A_{j} \times A_{k})^{(i)}$ ,分别称 $A_{1}, A_{2}, A_{3}$ 为该三元概念的外延、内涵和方式.

三元背景 $Κ$ 的所有三元概念构成的集合记为 $I (Κ)$ .

根据定义4和式(6)容易验证以下结论成立：

(1) $\forall (A_{1}, A_{2}, A_{3}) \in I (Κ)$ ， $\forall x_{l} \in K_{l}, l \in \{1,2, 3\}$ ，

若 $(x_{1}, x_{2}, x_{3}) \in (A_{1}, A_{2}, A_{3})$ 则 $(x_{1}, x_{2}, x_{3}) \in Y$ .

(2) $\forall (A_{1}, A_{2}, A_{3}), (B_{1}, B_{2}, B_{3}) \in I (Κ)$ ，若 $A_{i} \subseteq B_{i}, A_{j} \subseteq B_{j}$ 则 $A_{k} \supseteq B_{k}, \{i, j, k\} = \{1,2, 3\}$ .

Lehmann and Wille^[1]给出了构造三元概念的方法： $\forall X_{i} \subseteq K_{i}, X_{k} \subseteq K_{k}, \{i, j, k\} = \{1,2, 3\}$ ，定义 $A_{j} ≕ {X_{i}}^{(i, j, X_{k})}, A_{i} ≕ {A_{j}}^{(i, j, X_{k})}, A_{k} ≕ (A_{i} \times A_{j})^{(k)}$ ，则 $(A_{1}, A_{2}, A_{3}) \in I (Κ)$ .

王霞等^[13]在三元背景中定义了对象⁃条件三元概念，提出了一种基于对象⁃条件三元概念生成三元概念的简便方法.三元背景在经典形式背景（二元背景）上添加条件集，它可以描述在哪些条件下一个对象具有某个属性．一个三元背景由它的每一个非空条件子集可以确定一个二元背景.李俊余等^[14]研究了三元概念和经典形式概念（二元概念）之间的关系，定义了二元概念到三元概念的双射,从二元背景出发描述三元概念，并基于三元概念提出了由每个条件确定的二元背景的二元概念的方法．王霞等^[15]基于三元背景构造了条件属性蕴含形式背景,定义了形式概念、对象定向概念和属性定向概念，并给出了相应的概念格.

2 三元因子分析

设 $A$ 是一个 $n \times k$ 布尔矩阵， $B$ 是一个 $k \times m$ 布尔矩阵，则布尔矩阵乘积 $A \circ B$ 是一个 $n \times m$ 布尔矩阵，定义如下：

{(A \circ B)}_{i j} = \overset{k}{\underset{l = 1}{\lor}} A_{i l} \cdot B_{l j}

其中“ $\lor$ ”为逻辑或，“ $\cdot$ ”为逻辑与.

设 $C$ 为一个 $n \times m$ 布尔矩阵.若存在 $n \times k$ 布尔矩阵 $A$ 和 $k \times m$ 布尔矩阵 $B$ 使得 $C = A \circ B$ ，则称 $C$ 是可因子分解的.

定义5^[11] 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，若 $\exists F \subseteq I (Κ)$ 使 $Y = \underset{(A, B, C) \in F}{\cup} A \times B \times C$ ，

则称 $F$ 为三元背景 $Κ$ 的一个因子分解.若 $F$ 的基 $|F|$ 最小，则称 $F$ 为三元背景 $Κ$ 的一个最优因子分解，称 $F$ 中的元素为三元背景 $Κ$ 的(最优)因子.

布尔3d⁃矩阵(简称3d⁃矩阵)是一个长方体 $B_{p \times q \times r}$ ，其元素 $b_{i j k} \in \{0,1\}$ ， $i \in \{1,2, \dots, p\}$ ， $j \in \{1,2, \dots, q\}$ ， $k \in \{1,2, \dots, r\}$ .对于一个3d⁃矩阵 $B_{p \times q \times r}$ ，记 $B = B_{1} |\dots| B_{r}$ ，其中 $B_{k}$ ， $k \in \{1, \dots, r\}$ 为 $p \times q$ 布尔矩阵，称其为分层.

定义6^[11] 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，称因子 $(A_{1}, A_{2}, A_{3})$ 是强制性的当且仅当 $\exists (g, m, b) \in Y$ 使得 $(A_{1}, A_{2}, A_{3})$ 是唯一满足 $(g, m, b) \in (A_{1}, A_{2}, A_{3})$ 的三元概念.

定义7^[11] 设 $P$ 是一个 $p \times n$ 布尔矩阵， $Q$ 是一个 $q \times n$ 布尔矩阵， $R$ 是一个 $r \times n$ 布尔矩阵，布尔3d⁃矩阵乘积(简称为3d⁃矩阵乘积)定义如下：

{(P \circ Q \circ R)}_{i j k} = \overset{n}{\underset{l = 1}{\lor}} P_{i l} \cdot Q_{j l} \cdot R_{k l}

其中, $i \in \{1,2, \dots, p\}$ , $j \in \{1,2, \dots, q\},$ $k \in \{1,2,$

\dots, r\}

关于3d⁃矩阵乘积有如下两种等价的表示形式^[11]：

(1) {(P \circ Q \circ R)}_{i j k} = {(P * Q \circ R)}_{i j k} = \overset{n}{\underset{l = 1}{\lor}} {(P * Q)}_{(i j) l} \cdot R_{k l}

，其中

{(P * Q)}_{(i j) l} = P_{i l} \cdot Q_{j l}

(2) {(P \circ Q \circ R)}_{i j k} = {(P \circ Q * R)}_{i j k} = \overset{n}{\underset{l = 1}{\lor}} P_{i l} \cdot {(Q * R)}_{(j k) l}

，其中

{(Q * R)}_{(j k) l} = Q_{j l} \cdot R_{k l}

设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，以下假设 $K_{1} = \{1,2, \dots, p\}$ ， $K_{2} = \{1,2, \dots, q\}$ ， $K_{3} = \{1,2, \dots, r\}$ ，并将三元背景中“×”的位置记为1，没有“×”的位置记为0，则三元背景可看作是一个3d⁃矩阵 $B_{p \times q \times r}$ .

记：

F = \{(A_{1}, B_{1}, C_{1}), \dots, (A_{n}, B_{n}, C_{n})\} \subseteq I (Κ)

Belohlavek^[11]定义矩阵 $A_{F}$ ， $B_{F}$ ， $C_{F}$ ：

(A_{F})_{i l} = \{\begin{array}{l} 1, i \in A_{l} \\ 0, i \notin A_{l} \end{array}, 1 \leq i \leq p, 1 \leq l \leq n

(9)

(B_{F})_{j l} = \{\begin{array}{l} 1, j \in B_{l} \\ 0, j \notin B_{l} \end{array}, 1 \leq j \leq q, 1 \leq l \leq n

(10)

(C_{F})_{k l} = \{\begin{array}{l} 1, k \in C_{l} \\ 0, k \notin C_{l} \end{array}, 1 \leq k \leq r, 1 \leq l \leq n

(11)

定理1^[11] 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，B是对应的3d⁃矩阵，则 $\exists F \subseteq I (Κ)$ 使得 $B = A_{F} \circ B_{F} \circ C_{F}$ ，其中 $A_{F}, B_{F}, C_{F}$ 按式(9)至式(11)构造.

引理1 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $B$ 是对应的3d⁃矩阵，则 $F \subseteq I (Κ)$ 为三元背景 $Κ$ 的一个因子分解当且仅当 $B = A_{F} \circ B_{F} \circ C_{F}$ .

证明根据定义5知，F为三元背景 $Κ$ 的一个因子分解当且仅当 $Y = \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i}$ .即 $(i, j, k) \in Y$ 当且仅当存在 $(A_{l}, B_{l}, C_{l}) \in F$ 使得 $(i, j, k) \in A_{l} \times B_{l} \times C_{l}$ .由式(9)至式(11)知， $(i, j, k) \in A_{l} \times B_{l} \times C_{l}$ 等价于 $(A_{F})_{i l} = 1$ ， $(B_{F})_{j l} = 1$ ， $(C_{F})_{k l} = 1$ .这等价于 $(A_{F} * B_{F})_{(i j) l} = (A_{F})_{i l} \cdot (B_{F})_{j l} = 1$ ，且 $(A_{F} * B_{F})_{(i j) l} \cdot (C_{F})_{k l} = 1$ ，即 $(A_{F} * B_{F} \circ C_{F})_{i j k} = 1$ .因此等价于 $B = A_{F} \circ B_{F} \circ C_{F}$ .

证毕.

定理2^[11] 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $F \subseteq I (Κ)$ ， $B$ 是对应的3d⁃矩阵. $(A_{1}, A_{2}, A_{3})$ 是因子分解 $B = A_{F} \circ B_{F} \circ C_{F}$ 的强制性因子当且仅当 $\exists x_{l} \in K_{l}, l \in \{1,2, 3\}$ 使得：

(A_{1}, A_{2}, A_{3}) =

(x_{1}^{(1,2, x_{3}) (1,2, x_{3})}, x_{1}^{(1,2, x_{3})}, {(x_{1}^{(1,2, x_{3}) (1,2, x_{3})} \times x_{1}^{(1,2, x_{3})})}^{(3)}) =

(12)

(x_{2}^{(1,2, x_{3})}, x_{2}^{(1,2, x_{3}) (1,2, x_{3})}, {(x_{2}^{(1,2, x_{3})} \times x_{2}^{(1,2, x_{3}) (1,2, x_{3})})}^{(3)}) =

(13)

(x_{1}^{(1,3, x_{2}) (1,3, x_{2})}, {(x_{1}^{(1,3, x_{2}) (1,3, x_{2})} \times x_{1}^{(1,3, x_{2})})}^{(2)}, x_{1}^{(1,3, x_{2})}) =

(14)

(x_{3}^{(1,3, x_{2})}, {(x_{3}^{(1,3, x_{2})} \times x_{3}^{(1,3, x_{2}) (1,3, x_{2})})}^{(2)}, x_{3}^{(1,3, x_{2}) (1,3, x_{2})}) =

(15)

({(x_{2}^{(2,3, x_{1}) (2,3, x_{1})} \times x_{2}^{(2,3, x_{1})})}^{(1)}, x_{2}^{(2,3, x_{1}) (2,3, x_{1})}, x_{2}^{(2,3, x_{1})}) =

(16)

({(x_{3}^{(2,3, x_{1})} \times x_{3}^{(2,3, x_{1}) (2,3, x_{1})})}^{(1)}, x_{3}^{(2,3, x_{1})}, x_{3}^{(2,3, x_{1}) (2,3, x_{1})})

(17)

引理2 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $F \subseteq I (Κ)$ 是三元背景 $Κ$ 的一个因子分解， $(A_{1}, A_{2}, A_{3})$ 是F的强制性因子.则有：

(1)若 $(g, m, b) \in Y$ 使得 $(A_{1}, A_{2}, A_{3})$ 是唯一满足 $(g, m, b) \in (A_{1}, A_{2}, A_{3})$ 的三元概念，则：

\begin{array}{l} (A_{1}, A_{2}, A_{3}) = \\ (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) = \\ (m^{(1,2, b)}, m^{(1,2, b) (1,2, b)}, {(m^{(1,2, b)} \times m^{(1,2, b) (1,2, b)})}^{(3)}) = \\ (g^{(1,3, m) (1,3, m)}, {(g^{(1,3, m) (1,3, m)} \times g^{(1,3, m)})}^{(2)}, g^{(1,3, m)}) = \\ (b^{(1,3, m)}, {(b^{(1,3, m)} \times b^{(1,3, m) (1,3, m)})}^{(2)}, b^{(1,3, m) (1,3, m)}) = \\ ({(m^{(2,3, g) (2,3, g)} \times m^{(2,3, g)})}^{(1)}, m^{(2,3, g) (2,3, g)}, m^{(2,3, g)}) = \\ ({(b^{(2,3, g)} \times b^{(2,3, g) (2,3, g)})}^{(1)}, b^{(2,3, g)}, b^{(2,3, g) (2,3, g)}) \end{array}

(2)若 $\exists x_{l} \in K_{l}, l \in \{1,2, 3\}$ 使式(12)至式(17)成立，则 $(x_{1}, x_{2}, x_{3}) \in Y$ 使 $(A_{1}, A_{2}, A_{3})$ 是唯一满足 $(x_{1}, x_{2}, x_{3}) \in (A_{1}, A_{2}, A_{3})$ 的三元概念.

证明 (1)若 $(g, m, b) \in Y$ 使 $(A_{1}, A_{2}, A_{3})$ 是唯一满足 $(g, m, b) \in (A_{1}, A_{2}, A_{3})$ 的三元概念，则由定义4容易验证：

(g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) \in I (Κ)

根据式(7)和式(8)可知， $\forall (g, m, b) \in Y$ 有 $g \in g^{(1,2, b) (1,2, b)}, m \in g^{(1,2, b)}$ ，且 $\forall g_{0} \in g^{(1,2, b) (1,2, b)}$ 有

{g_{0}}^{(1,2, b)} \supseteq g^{(1,2, b)}

.因此，

\forall m_{0} \in g^{(1,2, b)}

有

m_{0} \in {g_{0}}^{(1,2, b)}

，

即 $(g_{0}, m_{0}, b) \in Y$ .从而， $\forall g_{0} \in g^{(1,2, b) (1,2, b)}$ ， $\forall m_{0} \in g^{(1,2, b)}$ 有 $(g_{0}, m_{0}, b) \in Y$ .结合式(4)可知，

b \in (g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})^{(3)}

.于是：

(g, m, b) \in (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)})

因此，

\begin{array}{l} (A_{1}, A_{2}, A_{3}) = \\ (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) \end{array}

成立.

类似地可以验证：

\begin{array}{l} (A_{1}, A_{2}, A_{3}) = \\ (m^{(1,2, b)}, m^{(1,2, b) (1,2, b)}, {(m^{(1,2, b)} \times m^{(1,2, b) (1,2, b)})}^{(3)}) = \\ (g^{(1,3, m) (1,3, m)}, {(g^{(1,3, m) (1,3, m)} \times g^{(1,3, m)})}^{(2)}, g^{(1,3, m)}) = \\ (b^{(1,3, m)}, {(b^{(1,3, m)} \times b^{(1,3, m) (1,3, m)})}^{(2)}, b^{(1,3, m) (1,3, m)}) = \\ ({(m^{(2,3, g) (2,3, g)} \times m^{(2,3, g)})}^{(1)}, m^{(2,3, g) (2,3, g)}, m^{(2,3, g)}) = \\ ({(b^{(2,3, g)} \times b^{(2,3, g) (2,3, g)})}^{(1)}, b^{(2,3, g)}, b^{(2,3, g) (2,3, g)}) \end{array}

(2)若 $\exists x_{l} \in K_{l}, l \in \{1,2, 3\}$ 使式(12)至式(17)成立，显然 $x_{1} \in x_{1}^{(1,2, x_{3}) (1,2, x_{3})}$ ， $x_{2} \in x_{2}^{(1,2, x_{3}) (1,2, x_{3})}$ ，

$x_{3} \in x_{3}^{(1,3, x_{2}) (1,3, x_{2})}$ .又根据式(12)至式(17)可得 $A_{1} =$

x_{1}^{(1,2, x_{3}) (1,2, x_{3})}, A_{2} = x_{2}^{(1,2, x_{3}) (1,2, x_{3})}, A_{3} = x_{3}^{(1,3, x_{2}) (1,3, x_{2})}

，所

以 $(x_{1}, x_{2}, x_{3}) \in (A_{1}, A_{2}, A_{3})$ ， $\forall (B_{1}, B_{2}, B_{3}) \in I (Κ)$ .

若 $(x_{1}, x_{2}, x_{3}) \in (B_{1}, B_{2}, B_{3})$ ，则根据定义4、式(7)和式(8)可知， $B_{2} = B_{1}^{(1,2, B_{3})} \subseteq x_{1}^{(1,2, x_{3})}$ ， $B_{1} = B_{2}^{(1,2, B_{3})} \subseteq x_{2}^{(1,2, x_{3})}$ ， $B_{3} =$ $B_{1}^{(1,3, B_{2})} \subseteq x_{1}^{(1,3, x_{2})}$ .又根据式(12)至式(17)可知， $(A_{1}, A_{2}, A_{3}) = (x_{2}^{(1,2, x_{3})}, x_{1}^{(1,2, x_{3})}, x_{1}^{(1,3, x_{2})})$ ，因此 $B_{l} \subseteq$ $A_{l}, l \in \{1,2, 3\}$ ，所以 $(B_{1}, B_{2}, B_{3}) = (A_{1}, A_{2}, A_{3})$ .

证毕.

由定义6、定理1和引理2可以直接得到下面的结论.

定理3 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $F \subseteq I (Κ)$ 是三元背景 $Κ$ 的一个因子分解， $(A_{1}, A_{2}, A_{3}) \in I (Κ)$ .则下列结论等价：

(1) $(A_{1}, A_{2}, A_{3})$ 是因子分解F的强制性因子.

(2) $\exists (g, m, b) \in Y$ 使得 $(A_{1}, A_{2}, A_{3})$ 是唯一满足 $(g, m, b) \in (A_{1}, A_{2}, A_{3})$ 的三元概念.

\begin{array}{l} (3) (A_{1}, A_{2}, A_{3}) = \\ (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) = \\ (m^{(1,2, b)}, m^{(1,2, b) (1,2, b)}, {(m^{(1,2, b)} \times m^{(1,2, b) (1,2, b)})}^{(3)}) = \\ (g^{(1,3, m) (1,3, m)}, {(g^{(1,3, m) (1,3, m)} \times g^{(1,3, m)})}^{(2)}, g^{(1,3, m)}) = \\ (b^{(1,3, m)}, {(b^{(1,3, m)} \times b^{(1,3, m) (1,3, m)})}^{(2)}, b^{(1,3, m) (1,3, m)}) = \\ ({(m^{(2,3, g) (2,3, g)} \times m^{(2,3, g)})}^{(1)}, m^{(2,3, g) (2,3, g)}, m^{(2,3, g)}) = \\ ({(b^{(2,3, g)} \times b^{(2,3, g) (2,3, g)})}^{(1)}, b^{(2,3, g)}, b^{(2,3, g) (2,3, g)}) \end{array}

推论1 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $F \subseteq I (Κ)$ 是三元背景 $Κ$ 的一个因子分解， $(A_{1}, A_{2}, A_{3}) \in I (Κ)$ .若 $\exists l \in \{1,2, 3\}$ 使 $|A_{l}| = 1$ ，则 $(A_{1}, A_{2}, A_{3})$ 是因子分解 $F$ 的强制性因子.

3 三元概念的一种约简方法

下面利用三元因子分解对三元概念进行约简.

3.1　三元概念约简的定义

定义8 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 是一个三元背景， $F \subseteq I (Κ)$ .若 $Y = \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i}$ ，则称F为保持三元背景 $Κ$ 不变的三元概念协调集.若进一步 $\forall (A, B, C) \in F$ 都有：

Y \neq \underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}

则称F为保持三元背景 $Κ$ 不变的三元概念约简.

由定义5和定义8可直接得到下面结论.

推论2 设 $Κ$ 为三元背景， $F \subseteq I (Κ)$ .则 $F$ 为保持三元背景 $Κ$ 不变的三元概念协调集当且仅当F为三元背景 $Κ$ 的一个因子分解.

定理4 设 $Κ$ 为三元背景，则总存在保持三元背景 $Κ$ 不变的三元概念约简.

证明根据推论2和定理1知，总存在保持三元背景 $Κ$ 不变的三元概念协调集，记为F.对 $\forall (A, B, C) \in F$ ，验证：

Y \neq \underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}

是否成立.若成立，则F为保持三元背景 $Κ$ 不变的三元概念约简；若 $\exists (A, B, C) \in F$ ，使得：

Y = \underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}

则F不是保持三元背景 $Κ$ 不变的三元概念约简， $F \ \{(A, B, C)\}$ 为保持三元背景 $Κ$ 不变的三元概念协调集.对 $F \ \{(A, B, C)\}$ 重复上述过程，由于 $K_{1}, K_{2}, K_{3}$ 均为有限集，所以F也为有限集，所以总能找到一个三元概念约简.

证毕.

注根据推论2可知，寻找三元概念协调集 $F \subseteq I (Κ)$ 有两种方法：一种是利用三元因子分解，首先根据式(9)至式(11)构造 $A_{F}, B_{F}, C_{F}$ ，再验证 $B = A_{F} \circ B_{F} \circ C_{F}$ 成立；另一种是直接利用三元概念约简的定义，首先计算 $\underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i}$ ，再验证 $Y = \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i}$ 成立.

推论3 设 $Κ$ 为三元背景， $F \subseteq I (Κ)$ ， $B$ 为对应的3d⁃矩阵.若 $F$ 为三元背景 $Κ$ 的三元概念协调集，则 $F$ 必包含 $B$ 的强制性因子.

例1表1给出了三元背景 $Κ = (K_{1}, K_{2}, K_{3},$

表1 三元背景 $Κ = (K_{1}, K_{2}, K_{3}, Y)$

Table 1 A triadic context $Κ = (K_{1}, K_{2}, K_{3}, Y)$

	1						2						3
	1	2	3	4	5	6	1	2	3	4	5	6	1	2	3	4	5	6
1	0	0	1	0	0	0	0	0	1	1	0	0	0	0	1	1	0	0
2	0	1	1	1	0	1	0	1	1	1	0	1	1	1	1	1	0	1
3	1	1	1	1	0	1	1	1	1	1	1	1	0	1	1	1	1	1
4	1	1	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1
5	1	1	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1
6	0	0	1	1	0	1	1	1	1	1	1	1	1	1	1	1	0	1

新窗口打开| 下载CSV

$Y)$ ，其中对象集 $K_{1} = \{1,2, 3,4, 5,6\}$ （左边第一列表示对象），属性集 $K_{2} = \{1,2, 3,4, 5,6\}$ ，条件集 $K_{3} = \{1,2, 3\}$ .

根据定义4计算表1三元背景 $Κ$ 的三元概念，分别为：

C 1 ≕ (\{1,2, 3,6\}, \{3\}, K_{3})

C 2 ≕ (\{2,3\}, \{2,3, 4,6\}, K_{3})

C 3 ≕ (\{3\}, \{1,2, 3,4, 6\}, \{1,2\})

C 4 ≕ (\{3,4, 5\}, \{1,2, 4,6\}, \{1,2\})

C 5 ≕ (\{2,3, 6\}, \{3,4, 6\}, K_{3})

C 6 ≕ (\{4,5\}, K_{2}, \{2,3\})

C 7 ≕ (\{2,3, 4,5\}, \{2,4, 6\}, K_{3})

C 8 ≕ (\{2,3, 4,5, 6\}, \{4,6\}, K_{3})

C 9 ≕ (K_{1}, \emptyset, K_{3})

C 10 ≕ (K_{1}, \{3,4\}, \{2,3\})

C 11 ≕ (\{2,3, 4,5, 6\}, \{2,3, 4,6\}, \{2,3\})

C 12 ≕ (\emptyset, K_{2}, K_{3})

C 13 ≕ (\{3,4, 5,6\}, K_{2}, \{2\})

C 14 ≕ (\{2,4, 5,6\}, \{1,2, 3,4, 6\}, \{3\})

C 15 ≕ (K_{1}, K_{2}, \emptyset)

C 16 ≕ (\{3,4, 5\}, \{2,3, 4,5.6\}, \{2,3\})

C 17 ≕ (\{4,5\}, \{1,2, 4,6\}, K_{3})

C 18 ≕ (\{4,5, 6\}, \{1,2, 3,4, 6\}, \{2,3\})

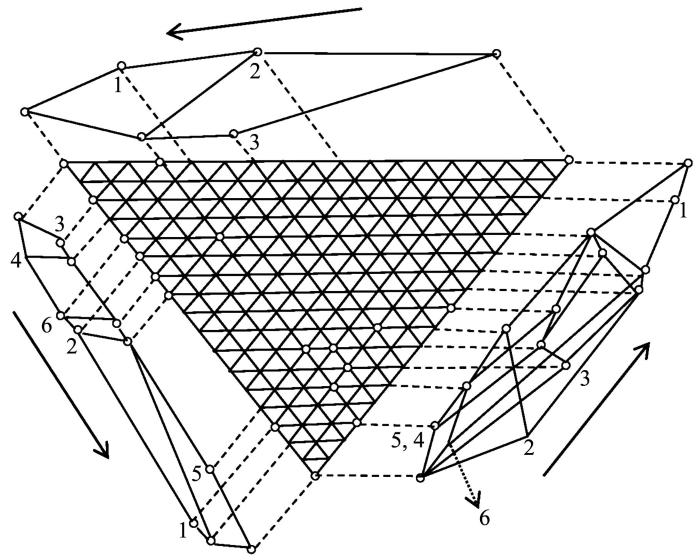
图1给出了三元概念的三元图表示，更直观地描述了上述所有18个三元概念.图1最上面的线图表示条件之间的关系，其中每一个圆圈表示一个三元概念的方式,它包含该圆圈处所示的条件及其右侧线段相连处圆圈所示的条件；左下方的线图表示属性之间的关系，其中每一个圆圈表示一个三元概念的内涵,它包含该圆圈处所示的属性及其左上方线段相连处圆圈所示的属性；右下方的线图表示对象之间的关系，其中每一个圆圈表示一个三元概念的外延,它包含该圆圈处所示的对象及其左下方线段相连处圆圈所示的对象；正中三角形中的每一个圆圈表示一个三元概念，它通过虚线分别与其外延、内涵和方式相连.如,正中间三角形中左上方第一个圆圈表示三元概念 $C 9 ≕ (K_{1}, \emptyset, K_{3})$ ,从上面数第一行左侧第二个圆圈表示三元概念 $C 10 ≕ (K_{1}, \{3,4\},$ $\{2,3\})$ .容易验证， $(1,3, 1)$ 只存在于三元概念 $C 1$ 中； $(1,4, 3)$ 只存在于三元概念 $C 10$ 中； $(6,5, 2)$ 只存在于三元概念 $C 13$ 中； $(2,1, 3)$ 只存在于三元概念 $C 14$ 中； $(3,5, 3)$ 只存在于三元概念 $C 16$ 中.因此， $C 1$ , $C 10$ ， $C 13$ , $C 14$ , $C 16$ 均为强制性因子，并由定理3可验证其他13个三元概念均不是强制性因子.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 三元概念 $I (Κ)$ 对应的三元图

Fig.1 The triadic diagram of the triadic concept $I (Κ)$

下面分别用三元因子分解法和三元概念约简定义法计算表1的三元概念约简.

方法一：三元因子分解法

令 $F_{1} = \{C 1, C 2, C 4, C 5, C 10, C 13, C 14, C 16\}$ ，根据式(9)至式(11)可得：

A_{F_{1}} = (\begin{matrix} 1 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 1 & 1 & 0 & 0 & 0 & 1 \end{matrix})

B_{F_{1}} = (\begin{matrix} 0 & 0 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 1 & 1 & 1 & 1 \end{matrix})

C_{F_{1}} = (\begin{matrix} 1 & 0 & 0 & 0 & 0 & 1 & 1 & 1 \\ 1 & 1 & 1 & 0 & 1 & 1 & 1 & 1 \\ 1 & 1 & 0 & 1 & 1 & 1 & 0 & 1 \end{matrix})

计算得：

A_{F_{1}} * B_{F_{1}} = (\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | & 1 & 1 & 1 & 1 & 0 & 1 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | & 0 & 0 & 0 & 0 & 0 & 0 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | & 1 & 1 & 1 & 1 & 0 & 1 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | & 1 & 1 & 1 & 1 & 0 & 1 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | & 1 & 1 & 1 & 1 & 0 & 1 & | \end{matrix}

\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 1 & 1 & 1 & 0 & 1 & | \\ 0 & 1 & 1 & 1 & 1 & 1 & | & 0 & 1 & 1 & 1 & 0 & 1 & | \\ 0 & 1 & 1 & 1 & 1 & 1 & | & 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 1 & 1 & 1 & 1 & 1 & | & 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & | & 0 & 0 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 & | & 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 1 & 0 & 1 & | & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & | & 0 & 0 & 1 & 1 & 0 & 1 \end{matrix})

于是有：

(A_{F_{1}} * B_{F_{1}}) \circ C_{F_{1}} =

(\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 1 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \end{matrix}) \lor

(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 1 & 0 & 0 & | \\ 0 & 0 & 1 & 1 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 0 \end{matrix}) \lor

(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | \\ 1 & 1 & 1 & 1 & 1 & 1 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}) \lor

(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 \end{matrix}) \lor

(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 1 & 1 & 1 & 1 & 1 & | \\ 0 & 1 & 1 & 1 & 1 & 1 & | \\ 0 & 1 & 1 & 1 & 1 & 1 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 1 & 1 & 1 & 1 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}) \lor

(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 1 & 1 & 1 & 0 & 1 & | \\ 0 & 1 & 1 & 1 & 0 & 1 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 1 & 1 & 1 & 0 & 1 & | \\ 0 & 1 & 1 & 1 & 0 & 1 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}) \lor

(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 1 & 1 & 0 & 1 & 0 & 1 & | \\ 1 & 1 & 0 & 1 & 0 & 1 & | \\ 1 & 1 & 0 & 1 & 0 & 1 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \\ 1 & 1 & 0 & 1 & 0 & 1 & | \\ 1 & 1 & 0 & 1 & 0 & 1 & | \\ 1 & 1 & 0 & 1 & 0 & 1 & | \\ 0 & 0 & 0 & 0 & 0 & 0 & | \end{matrix} \begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}) \lor

(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 & 1 \end{matrix} \begin{matrix} | & 0 & 0 & 0 & 0 & 0 & 0 \\ | & 0 & 0 & 1 & 1 & 0 & 1 \\ | & 0 & 0 & 1 & 1 & 0 & 1 \\ | & 0 & 0 & 0 & 0 & 0 & 0 \\ | & 0 & 0 & 0 & 0 & 0 & 0 \\ | & 0 & 0 & 1 & 1 & 0 & 1 \end{matrix} \begin{matrix} | & 0 & 0 & 0 & 0 & 0 & 0 \\ | & 0 & 0 & 1 & 1 & 0 & 1 \\ | & 0 & 0 & 1 & 1 & 0 & 1 \\ | & 0 & 0 & 0 & 0 & 0 & 0 \\ | & 0 & 0 & 0 & 0 & 0 & 0 \\ | & 0 & 0 & 1 & 1 & 0 & 1 \end{matrix}) =

(\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \end{matrix} \begin{matrix} | & 0 & 0 & 1 & 1 & 0 & 0 \\ | & 0 & 1 & 1 & 1 & 0 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \end{matrix} \begin{matrix} | & 0 & 0 & 1 & 1 & 0 & 0 \\ | & 1 & 1 & 1 & 1 & 0 & 1 \\ | & 0 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 0 & 1 \end{matrix})

又因为三元背景对应的3d⁃矩阵B恰好为：

(\begin{matrix} 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 \\ 1 & 1 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 & 1 \end{matrix} \begin{matrix} | & 0 & 0 & 1 & 1 & 0 & 0 \\ | & 0 & 1 & 1 & 1 & 0 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \end{matrix} \begin{matrix} | & 0 & 0 & 1 & 1 & 0 & 0 \\ | & 1 & 1 & 1 & 1 & 0 & 1 \\ | & 0 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 1 & 1 \\ | & 1 & 1 & 1 & 1 & 0 & 1 \end{matrix})

所以， $B = A_{F} \circ B_{F} \circ C F$ .即， $F_{1}$ 为表1中三元背景 $Κ$ 的三元概念协调集.

类似地，可进一步验证： $\forall (A_{j}, B_{j}, C_{j}) \in F_{1}$ ，

(A_{F_{1} \ \{(A_{j}, B_{j}, C_{j})\}} * B_{F_{1} \ \{(A_{j}, B_{j}, C_{j})\}}) \circ C_{F_{1} \ \{(A_{j}, B_{j}, C_{j})\}} \neq Y

即 $F_{1}$ 为三元背景 $Κ$ 的三元概念约简.

方法二：三元概念约简定义法

由于：

\begin{array}{l} \underset{(A_{i}, B_{i}, C_{i}) \in F_{1}}{\cup} A_{i} \times B_{i} \times C_{i} = \{(1,3, 1), (1,3, 2), \\ (1,4, 2), (1,4, 3), (2,2, 1), (2,3, 1), (2,4, 1), \\ (2,6, 1), (2,2, 2), (2,3, 2), (2,4, 2), (2,6, 2), \\ (2,1, 3), (2,2, 3), (2,3, 3), (2,4, 3), (2,6, 3), \\ (3,1, 1), (3,2, 1), (3,3, 1), (3,4, 1), (3,6, 1), \\ (3,1, 2), (3,2, 2), (3,3, 2), (3,4, 2), (3,5, 2), \\ (3,6, 2), (3,2, 3), (3,3, 3), (3,4, 3), (3,5, 3), \\ (3,6, 3), (4,1, 1), (4,2, 1), (4,4, 1), (4,6, 1), \end{array}

\begin{array}{l} (4,1, 2), (4,2, 2), (4,3, 2), (4,4, 2), (4,5, 2), \\ (4,6, 2), (4,1, 3), (4,2, 3), (4,3, 3), (4,4, 3), \\ (4,5, 3), (4,6, 3), (5,1, 1), (5,2, 1), (5,4, 1), \\ (5,6, 1), (5,1, 2), (5,2, 2), (5,3, 2), (5,4, 2), \\ (5,5, 2), (5,6, 2), (5,1, 3), (5,2, 3), (5,3, 3), \\ (5,4, 3), (5,5, 3), (5,6, 3), (6,3, 1), (6,4, 1), \\ (6,6, 1), (6,1, 2), (6,2, 2), (6,3, 2), (6,4, 2), \\ (6,5, 2), (6,6, 2), (6,1, 3), (6,2, 3), (6,3, 3), \\ (6,4, 3), (6,6, 3)\} = Y \end{array}

所以根据定义8可知， $F_{1}$ 为三元背景 $Κ$ 的三元概念协调集.进一步可验证， $\forall (A_{j}, B_{j}, C_{j}) \in F_{1}$ ，

\underset{(A_{i}, B_{i}, C_{i}) \in F \ \{A_{j}, B_{j}, C_{j}\}}{\cup} A_{i} \times B_{i} \times C_{i} \neq Y

即 $F_{1}$ 为三元背景 $Κ$ 的三元概念约简.

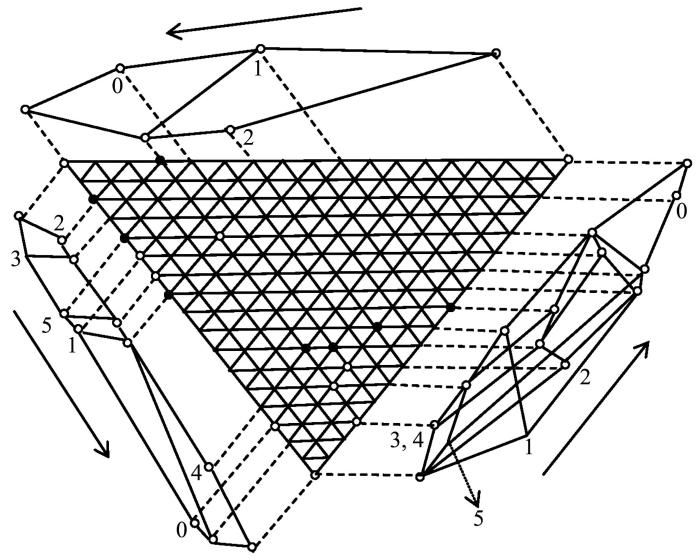
$F_{1}$ 对应的三元概念如图2所示，其中正中间三角形中黑点表示 $F_{1}$ 中的三元概念.令：

F_{2} = {C 1, C 2, C 4, C 8, C 10, C 13, C 14, C 16\}

F_{3} = {C 1, C 4, C 5, C 7, C 10, C 13, C 14, C 16\}

F_{4} = {C 1, C 4, C 7, C 8, C 10, C 13, C 14, C 16\}

F_{5} = {C 1, C 2, C 3, C 5,, C 10, C 13, C 14, C 16, C 17\}

F_{6} = {C 1, C 3, C 5, C 7, C 10, C 13, C 14, C 16, C 17\}

F_{7} = {C 1, C 2, C 3, C 8, C 10, C 13, C 14, C 16, C 17\}

F_{8} = {C 1, C 3, C 7, C 8, C 10, C 13, C 14, C 16, C 17\}

则可验证 $F_{2}, \dots, F_{8}$ 都是三元背景 $Κ$ 的三元概念约简，且三元背景 $Κ$ 只有这八个三元概念约简.表2是约简前后三元概念的对比，其中约简前共有18个三元概念，按 $F_{1}, \dots, F_{4}$ 约简后有八个三元概念，按 $F_{5}, \dots, F_{8}$ 约简后有九个三元概念.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 三元概念约简 $ℱ_{1}$ 对应的三元图

Fig.2 The triadic diagram of the concept reduct $F_{1}$

表2 约简前后三元概念对比

Table 2 Comparison of triadic concepts before and after reduction

约简前三元概念	约简后三元概念
约简前三元概念	约简 $F_{1}$	约简 $F_{2}$	约简 $F_{3}$	约简 $F_{4}$	约简 $F_{5}$	约简 $F_{6}$	约简 $F_{7}$	约简 $F_{8}$
C1,C2,…,C18	C1,C2,C4,C5,C10,C13,C14,C16	C1,C2,C4,C8,C10,C13,C14,C16	C1,C4,C5,C7,C10,C13,C14,C16	C1,C4,C7,C8,C10,C13,C14,C16	C1,C2,C3,C5,C10,C13,C14,C16，C17	C1,C3,C5,C7,C10,C13,C14,C16，C17	C1,C2,C3,C8,C10,C13,C14,C16，C17	C1,C3,C7,C8,C10,C13,C14,C16，C17

新窗口打开| 下载CSV

3.2　三元概念协调集的判定定理

定理5 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $F \subseteq I (Κ), G = I (Κ) \ F$ .则以下结论等价：

(1) $F$ 为三元背景 $Κ$ 的三元概念协调集；

(2) $\forall H \subseteq G, H \neq \emptyset$ ，

\underset{(A_{i}, B_{i}, C_{i}) \in H}{\cup} A_{i} \times B_{i} \times C_{i} \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

；

(3) $\forall (A, B, C) \in G$ ，

A \times B \times C \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

证明 $(1) \Rightarrow (2)$ .因为F为三元背景 $Κ$ 的三元概念协调集，所以根据定义8可得：

\underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j} = Y

又因为：

\begin{array}{l} Y = \underset{(A_{k}, B_{k}, C_{k}) \in G}{\cup} A_{k} \times B_{k} \times C_{k} ⋃ \\ \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j} \end{array}

于是有：

\underset{(A_{k}, B_{k}, C_{k}) \in G}{\cup} A_{k} \times B_{k} \times C_{k} \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

由于 $H \subseteq G, H \neq \emptyset$ ，所以：

\underset{(A_{i}, B_{i}, C_{i}) \in H}{\cup} A_{i} \times B_{i} \times C_{i} \subseteq \underset{(A_{k}, B_{k}, C_{k}) \in G}{\cup} A_{k} \times B_{k} \times C_{k}

因此

\underset{(A_{i}, B_{i}, C_{i}) \in H}{\cup} A_{i} \times B_{i} \times C_{i} \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

(2) \Rightarrow (3)

\forall (A, B, C) \in G

，令

H' = \{(A, B,

$C)\}$ ，则 $H' \subseteq G, H' \neq \emptyset$ .根据(2)可知：

\underset{(A_{i}, B_{i}, C_{i}) \in H'}{\cup} A_{i} \times B_{i} \times C_{i} \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

即： $A \times B \times C \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}$ .

(3) \Rightarrow (1)

.因为：

\forall (A, B, C) \in G, A \times B \times C \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

所以：

\underset{(A_{k}, B_{k}, C_{k}) \in G}{\cup} A_{k} \times B_{k} \times C_{k} \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

于是，

\begin{array}{l} Y = \underset{(A_{k}, B_{k}, C_{k}) \in G}{\cup} A_{k} \times B_{k} \times C_{k} ⋃ \\ \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j} \subseteq \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j} \end{array}

因此，

Y = \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j}

即F为三元背景 $Κ$ 的三元概念协调集.

证毕.

根据定义8和定理5可得如下三元概念约简的充要条件.

定理6 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $F \subseteq I (Κ), G = I (Κ) \ F$ .则 $F$ 为三元背景 $Κ$ 的三元概念约简当且仅当 $\forall (A, B, C) \in G,$

A \times B \times C \subseteq \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i}

且 $\forall (A_{l}, B_{l}, C_{l}) \in F$ ，

\begin{array}{l} \underset{(A_{j}, B_{j}, C_{j}) \in F \ \{(A_{l}, B_{l}, C_{l})\}}{\cup} A_{j} \times B_{j} \times C_{j} \neq \\ \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i} \end{array}

定义9 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景， $\forall x_{l} \in K_{l}, l \in \{1,2, 3\}$ ，称：

(x_{1}^{(1,2, x_{3}) (1,2, x_{3})}, x_{1}^{(1,2, x_{3})}, {(x_{1}^{(1,2, x_{3}) (1,2, x_{3})} \times x_{1}^{(1,2, x_{3})})}^{(3)})

为关于对象 $x_{1}$ 和条件 $x_{3}$ 的对象⁃条件三元概念.

称： $(x_{2}^{(1,2, x_{3})}, x_{2}^{(1,2, x_{3}) (1,2, x_{3})}, {(x_{2}^{(1,2, x_{3})} \times x_{2}^{(1,2, x_{3}) (1,2, x_{3})})}^{(3)})$

为关于属性 $x_{2}$ 和条件 $x_{3}$ 的属性⁃条件三元概念.

称： $(x_{1}^{(1,3, x_{2}) (1,3, x_{2})}, {(x_{1}^{(1,3, x_{2}) (1,3, x_{2})} \times x_{1}^{(1,3, x_{2})})}^{(2)}, x_{1}^{(1,3, x_{2})})$

为关于对象 $x_{1}$ 和属性 $x_{2}$ 的对象⁃属性三元概念.

称： $(x_{3}^{(1,3, x_{2})}, {(x_{3}^{(1,3, x_{2})} \times x_{3}^{(1,3, x_{2}) (1,3, x_{2})})}^{(2)}, x_{3}^{(1,3, x_{2}) (1,3, x_{2})})$

为关于条件 $x_{3}$ 和属性 $x_{2}$ 的条件⁃属性三元概念.

称： $({(x_{2}^{(2,3, x_{1}) (2,3, x_{1})} \times x_{2}^{(2,3, x_{1})})}^{(1)}, x_{2}^{(2,3, x_{1}) (2,3, x_{1})}, x_{2}^{(2,3, x_{1})})$

为关于属性 $x_{2}$ 和对象 $x_{1}$ 的属性⁃对象三元概念.

称： $({(x_{3}^{(2,3, x_{1})} \times x_{3}^{(2,3, x_{1}) (2,3, x_{1})})}^{(1)}, x_{3}^{(2,3, x_{1})}, x_{3}^{(2,3, x_{1}) (2,3, x_{1})})$

为关于条件 $x_{3}$ 和对象 $x_{1}$ 的条件⁃对象三元概念.

注

(x_{1}^{(1,2, x_{3}) (1,2, x_{3})}, x_{1}^{(1,2, x_{3})}, {(x_{1}^{(1,2, x_{3}) (1,2, x_{3})} \times x_{1}^{(1,2, x_{3})})}^{(3)})

与

({(x_{3}^{(2,3, x_{1})} \times x_{3}^{(2,3, x_{1}) (2,3, x_{1})})}^{(1)}, x_{3}^{(2,3, x_{1})}, x_{3}^{(2,3, x_{1}) (2,3, x_{1})})

不一定相等.如，在例1中取 $x_{1} = 1, x_{3} = 1$ ，则：

\begin{array}{l} (x_{1}^{(1,2, x_{3}) (1,2, x_{3})}, x_{1}^{(1,2, x_{3})}, {(x_{1}^{(1,2, x_{3}) (1,2, x_{3})} \times x_{1}^{(1,2, x_{3})})}^{(3)}) = \\ (\{3,4, 5\}, \{1,2, 4,6\}, \{1,2\}) \end{array}

而

\begin{array}{l} ({(x_{3}^{(2,3, x_{1})} \times x_{3}^{(2,3, x_{1}) (2,3, x_{1})})}^{(1)}, x_{3}^{(2,3, x_{1})}, x_{3}^{(2,3, x_{1}) (2,3, x_{1})}) = \\ (\{4,5\}, \{1,2, 4,6\}, K_{3}) \end{array}

同样的，

(x_{1}^{(1,3, x_{2}) (1,3, x_{2})}, {(x_{1}^{(1,3, x_{2}) (1,3, x_{2})} \times x_{1}^{(1,3, x_{2})})}^{(2)}, x_{1}^{(1,3, x_{2})})

与

({(x_{2}^{(2,3, x_{1}) (2,3, x_{1})} \times x_{2}^{(2,3, x_{1})})}^{(1)}, x_{2}^{(2,3, x_{1}) (2,3, x_{1})}, x_{2}^{(2,3, x_{1})})

不一定相等；

(x_{2}^{(1,2, x_{3})}, x_{2}^{(1,2, x_{3}) (1,2, x_{3})}, {(x_{2}^{(1,2, x_{3})} \times x_{2}^{(1,2, x_{3}) (1,2, x_{3})})}^{(3)})

与

(x_{3}^{(1,3, x_{2})}, {(x_{3}^{(1,3, x_{2})} \times x_{3}^{(1,3, x_{2}) (1,3, x_{2})})}^{(2)}, x_{3}^{(1,3, x_{2}) (1,3, x_{2})})

不一定相等.

记：

\begin{array}{l} O C (Κ) = \\ \{(x_{1}^{(1,2, x_{3}) (1,2, x_{3})}, x_{1}^{(1,2, x_{3})}, {(x_{1}^{(1,2, x_{3}) (1,2, x_{3})} \times x_{1}^{(1,2, x_{3})})}^{(3)})| x_{1} \in K_{1}, x_{3} \in K_{3}\} \end{array}

\begin{array}{l} A C (Κ) = \\ \{(x_{2}^{(1,2, x_{3})}, x_{2}^{(1,2, x_{3}) (1,2, x_{3})}, {(x_{2}^{(1,2, x_{3})} \times x_{2}^{(1,2, x_{3}) (1,2, x_{3})})}^{(3)})| x_{2} \in K_{2}, x_{3} \in K_{3}\} \end{array}

\begin{array}{l} O A (Κ) = \\ \{(x_{1}^{(1,3, x_{2}) (1,3, x_{2})}, {(x_{1}^{(1,3, x_{2}) (1,3, x_{2})} \times x_{1}^{(1,3, x_{2})})}^{(2)}, x_{1}^{(1,3, x_{2})})| x_{1} \in K_{1}, x_{2} \in K_{2}\} \end{array}

\begin{array}{l} C A (Κ) = \\ \{(x_{3}^{(1,3, x_{2})}, {(x_{3}^{(1,3, x_{2})} \times x_{3}^{(1,3, x_{2}) (1,3, x_{2})})}^{(2)}, x_{3}^{(1,3, x_{2}) (1,3, x_{2})})| x_{2} \in K_{2}, x_{3} \in K_{3}\} \end{array}

\begin{array}{l} A O (Κ) = \\ \{({(x_{2}^{(2,3, x_{1}) (2,3, x_{1})} \times x_{2}^{(2,3, x_{1})})}^{(1)}, x_{2}^{(2,3, x_{1}) (2,3, x_{1})}, x_{2}^{(2,3, x_{1})})| x_{1} \in K_{1}, x_{2} \in K_{2}\} \end{array}

\begin{array}{l} C O (Κ) = \\ \{({(x_{3}^{(2,3, x_{1})} \times x_{3}^{(2,3, x_{1}) (2,3, x_{1})})}^{(1)}, x_{3}^{(2,3, x_{1})}, x_{3}^{(2,3, x_{1}) (2,3, x_{1})})| x_{1} \in K_{1}, x_{3} \in K_{3}\} \end{array}

定义9给出了六类特殊的三元概念，下面考虑这六类三元概念与三元概念协调集的关系.

定理7 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，则 $O C (Κ)$ ， $A C (Κ)$ ， $O A (Κ)$ ， $C A (Κ)$ ， $A O (Κ)$ 和 $C O (Κ)$ 均为三元背景 $Κ$ 的三元概念协调集.

证明因为 $\forall (g, m, b) \in Y$ 有：

\begin{array}{l} (g, m, b) \in \\ (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) \end{array}

且有

\begin{array}{l} (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) \in \\ O C (Κ) \end{array}

所以

(g, m, b) \in \underset{(A_{i}, B_{i}, C_{i}) \in O C (Κ)}{\cup} A_{i} \times B_{i} \times C_{i}

即， $O C (Κ)$ 为三元背景 $Κ$ 的三元概念协调集.

类似地可以证明 $A C (Κ)$ , $O A (Κ)$ , $C A (Κ)$ , $A O (Κ)$ , $C O (Κ)$ 也都是三元背景 $Κ$ 的三元概念协调集.

证毕.

由定理2可直接得到以下结论：

推论4 设 $Κ$ 为三元背景， $(A_{1}, A_{2}, A_{3}) \in I (Κ)$

是强制性因子当且仅当

\begin{array}{l} (A_{1}, A_{2}, A_{3}) \in \\ O C (Κ) ⋂ A C (Κ) ⋂ O A (Κ) ⋂ \\ C O (Κ) ⋂ C A (Κ) ⋂ A O (Κ) \end{array}

例2（续例1）根据式(7)和式(8)计算表1中三元背景的六类三元概念，得：

O C (Κ) = \{C 1, C 2, C 3, C 4, C 5, C 6, C 10, C 13, C 14, C 16\}

A C (Κ) = \{C 1, C 4, C 7, C 8, C 10, C 11, C 12, C 13, C 14, C 16\}

O A (Κ) = \{C 1, C 4, C 7, C 8, C 10, C 11, C 13, C 14, C 15, C 16, C 17, C 18\}

C A (Κ) = \{C 1, C 4, C 7, C 8, C 10, C 11, C 12, C 13, C 14, C 16\}

A O (Κ) = \{C 1, C 2, C 3, C 5, C 6, C 10, C 13, C 14, C 16, C 17, C 18\}

C O (Κ) = \{C 1, C 2, C 3, C 5, C 6, C 10, C 13, C 14, C 16, C 17\}

对比例1的八个约简容易得出：

\begin{array}{l} F_{1} \subset O C (Κ), F_{4} \subset A C (Κ), F_{4} \subset O A (Κ), \\ F_{4} \subset C A (Κ), F_{5} \subset A O (Κ), F_{5} \subset C O (Κ) \end{array}

所以 $O C (Κ)$ , $A C (Κ)$ , $O A (Κ)$ , $C A (Κ)$ , $A O (Κ)$ , $C O (Κ)$ 均为表1中三元背景 $Κ$ 的三元概念协调集.且

\begin{array}{l} O C (Κ) ⋂ A C (Κ) ⋂ O A (Κ) ⋂ C O (Κ) ⋂ C A (Κ) ⋂ \\ A O (Κ) = \{C 1, C 10, C 13, C 14, C 16\} \end{array}

恰好为三元背景 $Κ$ 的所有强制性因子.

3.3　三元概念特征

根据表2可知，三元概念 $C 1, C 10, C 13, C 14, C 16$ 属于所有的约简，而三元概念 $C 6, C 9, C 11, C 12, C 15, C 18$ 不属于任意一个约简，其余的每一个三元概念必属于某个约简且存在某个约简不包含该三元概念.也就是说，在保持三元背景中所有三元关系不变时有些三元概念是必不可少的，如 $C 1, C 10, C 13, C 14, C 16$ ；有些三元概念是绝对不必要的，如 $C 6, C 9, C 11,$

$C 12, C 15,$ $C 18$ ；有些三元概念是相对必要的，如 $C 2, C 3, \dots, C 5$ 等.本节将详细研究三元概念的这些特征.

定义10 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，记 $T = \{F_{i}| i \in τ, τ 为指标集\}$ 为三元背景 $Κ$ 的三元概念约简的集合，现将三元概念分为以下三类：

(1)核心三元概念集 $C = \underset{i \in τ}{\cap} F_{i}$ ；

(2)相对必要三元概念集 $K = \underset{i \in τ}{\cup} F_{i} - \underset{i \in τ}{\cap} F_{i}$ ；

(3)不必要三元概念集 $U = I (Κ) - \underset{i \in τ}{\cup} F_{i}$ .

定理8 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 是一个三元背景，记 $T = \{F_{i}| i \in τ, τ 为指标集\}$ 为三元背景 $Κ$ 的三元概念约简的集合， $(A, B, C) \in I (Κ)$ ，则下列结论等价：

(1) $(A, B, C)$ 为核心三元概念；

(2) $\underset{(A_{i}, B_{i}, C_{i}) \in I (Κ) \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i} \neq Y$ ；

(3) $\exists (g, m, b) \in Y$ 使得 $(A, B, C)$ 是唯一满足 $(g, m, b) \in (A, B, C)$ 的三元概念；

(4) $(A, B, C)$ 是强制性因子；

（5）

\begin{array}{l} (A, B, C) = \\ (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) = \\ (m^{(1,2, b)}, m^{(1,2, b) (1,2, b)}, {((m^{(1,2, b)} \times m^{(1,2, b) (1,2, b)}))}^{(3)}) = \\ (g^{(1,3, m) (1,3, m)}, {(g^{(1,3, m) (1,3, m)} \times g^{(1,3, m)})}^{(2)}, g^{(1,3, m)}) = \\ (b^{(1,3, m)}, {(b^{(1,3, m)} \times b^{(1,3, m) (1,3, m)})}^{(2)}, b^{(1,3, m) (1,3, m)}) = \\ ({(m^{(2,3, g) (2,3, g)} \times m^{(2,3, g)})}^{(1)}, m^{(2,3, g) (2,3, g)}, m^{(2,3, g)}) = \\ ({(b^{(2,3, g)} \times b^{(2,3, g) (2,3, g)})}^{(1)}, b^{(2,3, g)}, b^{(2,3, g) (2,3, g)}) \end{array}

即

\begin{array}{l} (A, B, C) \in \\ O C (Κ) ⋂ A C (Κ) ⋂ O A (Κ) ⋂ \\ C A (Κ) ⋂ A O (Κ) ⋂ C O (Κ) \end{array}

证明 $(1) \Rightarrow (2)$ .若 $(A, B, C)$ 为核心三元概念，则根据定义10知，对任意的三元背景 $Κ$ 的三元概念约简 $F$ 都有 $(A, B, C) \in F$ .并且由定义8可得：

\begin{array}{l} Y = \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i} \neq \\ \underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i} \end{array}

若：

Y = \underset{(A_{i}, B_{i}, C_{i}) \in I (Κ) \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}

则存在三元概念约简 $F_{0} \subseteq I (Κ) \ \{(A, B, C)\}$ ，矛盾!所以：

\underset{(A_{i}, B_{i}, C_{i}) \in I (Κ) \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i} \neq Y

(2) \Rightarrow (3)

.由于：

\underset{(A_{i}, B_{i}, C_{i}) \in I (Κ) \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i} \neq Y

则必存在 $(g, m, b) \in Y$ 使得：

(g, m, b) \notin \underset{(A_{i}, B_{i}, C_{i}) \in I (Κ) \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}

因此 $(g, m, b) \in (A, B, C)$ 且 $\forall (A_{0}, B_{0}, C_{0}) \in$ $I (Κ)$ ，

若 $(A_{0}, B_{0}, C_{0}) \neq (A, B, C)$ 则 $(g, m, b) \notin (A_{0}, B_{0},$

$C_{0})$ .即 $(A, B, C)$ 是唯一满足 $(g, m, b) \in (A, B, C)$ 的三元概念.

由定理3可知， $(3) \Rightarrow (4)$ 和 $(4) \Rightarrow (5)$ 成立.

(5) \Rightarrow (1)

.若：

\begin{array}{l} (A, B, C) = \\ (g^{(1,2, b) (1,2, b)}, g^{(1,2, b)}, {(g^{(1,2, b) (1,2, b)} \times g^{(1,2, b)})}^{(3)}) = \\ (m^{(1,2, b)}, m^{(1,2, b) (1,2, b)}, {(m^{(1,2, b)} \times m^{(1,2, b) (1,2, b)})}^{(3)}) = \\ (g^{(1,3, m) (1,3, m)}, {(g^{(1,3, m) (1,3, m)} \times g^{(1,3, m)})}^{(2)}, g^{(1,3, m)}) = \\ (b^{(1,3, m)}, {(b^{(1,3, m)} \times b^{(1,3, m) (1,3, m)})}^{(2)}, b^{(1,3, m) (1,3, m)}) = \\ ({(m^{(2,3, g) (2,3, g)} \times m^{(2,3, g)})}^{(1)}, m^{(2,3, g) (2,3, g)}, m^{(2,3, g)}) = \\ ({(b^{(2,3, g)} \times b^{(2,3, g) (2,3, g)})}^{(1)}, b^{(2,3, g)}, b^{(2,3, g) (2,3, g)}) \end{array}

由定理3知， $(g, m, b) \in Y$ 满足 $(g, m, b) \in$ $(A,$ $B, C)$ 且 $\forall (A_{0}, B_{0}, C_{0}) \in I (Κ)$ ，若 $(g, m, b) \in$ $(A_{0},$ $B_{0}, C_{0})$ ，则 $(A_{0}, B_{0}, C_{0}) = (A, B,$

$C)$ .又因为对任意三元概念约简 $F$ ，

Y = \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i}

所以，

(g, m, b) \in \underset{(A_{i}, B_{i}, C_{i}) \in F}{\cup} A_{i} \times B_{i} \times C_{i}

于是 $\exists (A_{l}, B_{l},$ $C_{l}) \in F$ 使得 $(g, m, b) \in (A_{l}, B_{l}, C_{l})$ ，因此 $(A_{l}, B_{l},$ $C_{l}) = (A, B, C)$ ，即 $(A, B, C) \in F$ ，所以 $(A, B, C)$ 为核心三元概念.

证毕.

定理9 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，S为三元背景 $Κ$ 的三元概念协调集构成的集合. $(A, B, C) \in I (Κ)$ 为不必要三元概念当且仅当

A \times B \times C \subseteq \underset{F \in S}{\cap} \{\underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}\}

证明充分性.因为：

A \times B \times C \subseteq \underset{F \in S}{\cap} \{\underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}\}

所以 $\forall (g, m, b) \in (A, B, C)$ 有：

(g, m, b) \in \underset{F \in S}{\cap} \{\underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}\}

即，对任意的三元概念协调集 $F$ ，必存在 $(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}$ 使得 $(g, m, b) \in (A_{i},$

B_{i}, C_{i})

，所以：

\begin{array}{l} \underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i} = \\ \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j} = Y \end{array}

则 $F \ {(A, B, C)} \in S$ .因此， $(A, B, C)$ 必不属于任何的三元概念约简.即， $(A, B, C)$ 为不必要三元概念.

必要性.若 $(A, B, C)$ 为不必要三元概念，则对任意的三元概念协调集 $F$ ，

\begin{array}{l} \underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i} = \\ \underset{(A_{j}, B_{j}, C_{j}) \in F}{\cup} A_{j} \times B_{j} \times C_{j} = Y \end{array}

所以 $\forall (g, m, b) \in (A, B, C)$ 必存在 $(A_{i}, B_{i}, C_{i}) \in$

$F \ \{(A, B, C)\}$ 使得 $(g, m, b) \in (A_{i}, B_{i}, C_{i})$ ，因此：

(g, m, b) \in \underset{F \in S}{\cap} \{\underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}\}

即：

A \times B \times C \subseteq \underset{F \in S}{\cap} \{\underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}\}

证毕.

由定义10、定理8和定理9可直接得到相对必要三元概念的充要条件.

定理10 设 $Κ = (K_{1}, K_{2}, K_{3}, Y)$ 为三元背景，S为三元背景 $Κ$ 的三元概念协调集构成的集合. $(A, B, C) \in I (Κ)$ 为相对必要三元概念当且仅当：

\underset{(A_{i}, B_{i}, C_{i}) \in I (Κ) \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i} = Y

且

A \times B \times C ⊄ \underset{F \in S}{\cap} \{\underset{(A_{i}, B_{i}, C_{i}) \in F \ \{(A, B, C)\}}{\cup} A_{i} \times B_{i} \times C_{i}\}

例3（续例1）根据定理8至定理10可将例1中的18个三元概念分类如下：

核心三元概念集：

C = \{C 1, C 10, C 13, C 14, C 16\}

相对必要三元概念集：

K = \{C 2, C 3, C 4, C 5, C 7, C 8, C 17\}

不必要三元概念集：

U = \{C 6, C 9, C 11, C 12, C 15, C 18\}

4 结论

本文考虑在保持三元背景不变的前提下利用三元因子分解对三元概念进行约简.该方法保留尽可能少的三元概念，同时又用这些三元概念完整的反映原始三元背景中包含的数据间的关系.

Tang et al^[16]定义了三元决策形式背景，并基于蕴含规则提出了三元概念的属性约简的定义和方法.该方法使原有的约束决策规则更加紧凑，能更好地对数据进行决策分析，但可能会丢失形式背景中的部分信息.如何将三元因子分析与三元决策形式背景相结合考虑三元概念的简化以及基于可辨识矩阵的三元概念约简的方法与算法设计将是我们进一步要研究的问题.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Lehmann

，Wille

A triadic approach to formal concept analysis

∥Ellis G，Levinson R，Rich W，et al. Conceptual Structures：Applications，Implementation and Theory. Springer Berlin Heidelberg，1995：32-43.

[本文引用: 5]

[2]

Ganter

，Wille

Formal concept analysis：mathematical foundations

Springer Berlin Heidelberg，1999，269.

[本文引用: 4]

[3]

Wille

Restructuring lattice theory：an approach based on hierarchies of concepts

∥Rival I. Ordered Sets. Springer Berlin Heidelberg，1982：445-470.

[本文引用: 1]

[4]

Keprt

，Snášel

Binary factor analysis with help of formal concepts

∥Snasel V，Belohlavek R. Proceedings of the CLA 2004 International Workshop on Concept Lattices and their Applications. Ostrava，Czech Republic：CEUR⁃WS.org，2004：90-101.

[本文引用: 1]

[5]

Bělohlávek

，Vychodil

On Boolean factor analysis with formal concepts as factors

∥Proceedings of SCIS&ISIS 2006. Tokyo，Japan：Japan Society for Fuzzy Theory and Intelligent Informatics，2006：1054-1059.

[6]

Belohlavek

，Vychodil

Discovery of optimal factors in binary data via a novel method of matrix decomposition

Journal of Computer and System Sciences，2010，76(1)：3-20.

[本文引用: 1]

[7]

Belohlavek

，Vychodil

Optimal factorization of three⁃way binary data

∥2010 IEEE International Conference on Granular Computing. San Jose，CA，USA：IEEE，2010：61-66.

[本文引用: 1]

[8]

Glodeanu

Factorization methods of binary，triadic，real and fuzzy data

Informatica，2011，56(2)：81-86.

[9]

Belohlavek

，Glodeanu

，Vychodil

Optimal factorization of three⁃way binary data using triadic concepts

Order，2013，30(2)：437-454.

[10]

Glodeanu

C V

Tri⁃ordinal factor analysis

∥Cellier P，Distel F，Ganter B. Formal Concept Analysis. Springer Berlin Heidelberg，2013：125-140.

[11]

Glodeanu

C V

Triadic factor analysis

∥Marzena K，Sergei A O. Proceedings of the 7^th International Conference on Concept Lattices and Their Applications. Sevilla，Spain：CEUR⁃WS.org，2010：127-138.

[本文引用: 8]

[12]

曹丽，魏玲，祁建军.

保持二元关系不变的概念约简

模式识别与人工智能，2018，31(6)：516-524.

[本文引用: 1]

Cao

，Wei

，Qi

J J

Concept reduction preserving binary relations

Pattern Recognition and Artificial Intelligence，2018，31(6)：516-524.

[本文引用: 1]

[13]

王霞，江山，李俊余等.

三元概念的一种构造方法

计算机研究与发展，2019，56(4)：844-853.

[本文引用: 1]

Wang

，Jiang

，Li

J Y

，et al.

A construction method of triadic concepts

Journal of Computer Research and Development，2019，56(4)：844-853.

[本文引用: 1]

[14]

李俊余，朱荣杰，王霞等.

三元概念与形式概念的关系

南京大学学报(自然科学)，2018，54(4)：786-793.

[本文引用: 1]

J Y

，Zhu

R J

，Wang

，et al.

The relationship between triadic concepts and formal concepts

Journal of Nanjing University (Natural Science)，2018，54(4)：786-793.

[本文引用: 1]

[15]

王霞，谭斯文，李俊余等.

基于条件属性蕴含的概念格构造及简化

南京大学学报(自然科学)，2019，55(4)：553-563.

[本文引用: 1]

Wang

，Tan

S W

，Li

J Y

，et al.

Constructions and simplifications of concept lattices based on conditional attribute implications

Journal of Nanjing University (Natural Sciences)，2019，55(4)：553-563.

[本文引用: 1]

[16]

Tang

Y Q

，Fan

，Li

J H

An information fusion technology for triadic decision contexts

International Journal of Machine Learning and Cybernetics，2016，7(1)：13-24.

[本文引用: 1]

A triadic approach to formal concept analysis

1995

... 1995年,Lehmann and Wille^[1]提出形式概念的三维方法，即三元概念分析，它的研究对象是由对象集、属性集、条件集和三元关系构成的三元背景.三元概念分析的另一个基本概念是由外延、内涵和方式构成的一个三元组，即三元概念.三元概念分析从形式上来看类似形式概念分析^[2-3]，但是有关三元概念分析的研究与发展远不如形式概念分析.当三元背景中数据量比较大时，三元概念可能也会随之变得很多，那么三元概念的三元图表示以及三元概念的语意解释也会变得更加繁琐，这在一定程度上制约了三元概念分析的理论研究和应用.因此，为了能更好地理解三元概念的涵义并从中提取有价值的信息，有必要对三元概念做适当的约简. ...

... 定义3^[1] 称

Κ = (K_{1}, K_{2}, K_{3}, Y)

为三元背景，其中

K_{1}, K_{2}, K_{3}

为非空集合，Y为

K_{1}, K_{2}, K_{3}

之间的关系，即

Y \subseteq K_{1} \times K_{2} \times K_{3}

.分别称

K_{1}, K_{2},

...

\{1,2, 3\}

，且

j < k, X \subseteq K_{i}, Z \subseteq K_{j} \times K_{k}

，Lehmann and Wille^[1]定义了(i)⁃诱导算子： ...

... 定义4^[1] 设

Κ = (K_{1}, K_{2}, K_{3}, Y)

为三元背景，称

(A_{1}, A_{2}, A_{3})

为三元背景K的一个三元概念.如果对

\{i, j, k\} = \{1,2, 3\}

，

j < k

,且

A_{i} \subseteq K_{i}

有

A_{i} = (A_{j} \times A_{k})^{(i)}

,分别称

A_{1}, A_{2}, A_{3}

为该三元概念的外延、内涵和方式. ...

... Lehmann and Wille^[1]给出了构造三元概念的方法：

\forall X_{i} \subseteq K_{i}, X_{k} \subseteq K_{k}, \{i, j, k\} = \{1,2, 3\}

，定义

A_{j} ≕ {X_{i}}^{(i, j, X_{k})}, A_{i} ≕ {A_{j}}^{(i, j, X_{k})}, A_{k} ≕ (A_{i} \times A_{j})^{(k)}

，则

(A_{1}, A_{2}, A_{3}) \in I (Κ)

. ...

Formal concept analysis：mathematical foundations

1999

... 定义1^[2] 称

(G, M, I)

为形式背景，其中

G

是一个对象集，

M

是一个属性集，

I

是

G

和

M

之间的一个关系.分别称

G

和

M

的元素为对象和属性. ...

... 定义2^[2] 设

(G, M, I)

为形式背景，

X \subseteq G

，

B \subseteq M

，若二元组

(X, B)

满足

X' = B

，

B' = X

，则称

(X, B)

为形式概念，其中, ...

... 性质1^[2] 设

(G, M, I)

为形式背景，

X, X_{1}, X_{2}

为任意的对象子集,

B, B_{1}, B_{2}

为任意的属性子集，则有下列几条性质成立： ...

Restructuring lattice theory：an approach based on hierarchies of concepts

1982

Binary factor analysis with help of formal concepts

2004

... 目前，形式概念分析与布尔因子分析相结合^[4-6]、三元形式概念分析与布尔因子分析相结合^[7-11]均取得了一些很好的研究成果.因子分析最早是由英国心理学家斯皮尔曼提出的，它的基本目的是用少数几个因子或类别线性地描述许多指标或因素之间的联系，这几个因子或类别能够反映原始因素之间的主要信息.布尔因子分析主要是针对布尔数据的一种因子分析方法，它的主要目的是寻找

m

个因子来表示原始的

p

个变量，要求

m

远远小于

p

. ...

On Boolean factor analysis with formal concepts as factors

2006

Discovery of optimal factors in binary data via a novel method of matrix decomposition

2010

m

个因子来表示原始的

p

个变量，要求

m

远远小于

p

. ...

Optimal factorization of three?way binary data

2010

m

个因子来表示原始的

p

个变量，要求

m

远远小于

p

. ...

Factorization methods of binary，triadic，real and fuzzy data

2011

Optimal factorization of three?way binary data using triadic concepts

2013

Tri?ordinal factor analysis

2013

Triadic factor analysis

2010

m

个因子来表示原始的

p

个变量，要求

m

远远小于

p

. ...

... 定义5^[11] 设

Κ = (K_{1}, K_{2}, K_{3}, Y)

为三元背景，若

\exists F \subseteq I (Κ)

使

Y = \underset{(A, B, C) \in F}{\cup} A \times B \times C

， ...

... 定义6^[11] 设

Κ = (K_{1}, K_{2}, K_{3}, Y)

为三元背景，称因子

(A_{1}, A_{2}, A_{3})

是强制性的当且仅当

\exists (g, m, b) \in Y

使得

(A_{1}, A_{2}, A_{3})

是唯一满足

(g, m, b) \in (A_{1}, A_{2}, A_{3})

的三元概念. ...

... 定义7^[11] 设

P

是一个

p \times n

布尔矩阵，

Q

是一个

q \times n

布尔矩阵，

R

是一个

r \times n

布尔矩阵，布尔3d⁃矩阵乘积(简称为3d⁃矩阵乘积)定义如下： ...

... 关于3d⁃矩阵乘积有如下两种等价的表示形式^[11]： ...

... Belohlavek^[11]定义矩阵

A_{F}

，

B_{F}

，

C_{F}

： ...

... 定理1^[11] 设

Κ = (K_{1}, K_{2}, K_{3}, Y)

为三元背景，B是对应的3d⁃矩阵，则

\exists F \subseteq I (Κ)

使得

B = A_{F} \circ B_{F} \circ C_{F}

，其中

A_{F}, B_{F}, C_{F}

按式(9)至式(11)构造. ...

... 定理2^[11] 设

Κ = (K_{1}, K_{2}, K_{3}, Y)

为三元背景，

F \subseteq I (Κ)

，

B

是对应的3d⁃矩阵.

(A_{1}, A_{2}, A_{3})

是因子分解

B = A_{F} \circ B_{F} \circ C_{F}

的强制性因子当且仅当

\exists x_{l} \in K_{l}, l \in \{1,2, 3\}

使得： ...

保持二元关系不变的概念约简

2018

... 曹丽等^[12]基于布尔因子分析提出了保持二元关系不变的概念约简，该方法在保持形式背景的二元关系不变的前提下对形式概念进行约简.受此启发，本文考虑利用三元因子分析来研究三元概念的约简问题.首先，定义基于三元因子分析的三元概念约简的概念，给出三元因子分解和三元概念协调集的关系，并通过实例给出利用因子分解法和定义法寻找三元概念约简的过程.最后给出三元概念协调集的判断方法，并对三元概念进行分类，给出每类三元概念的判定方法. ...

保持二元关系不变的概念约简

2018

三元概念的一种构造方法

2019

... 王霞等^[13]在三元背景中定义了对象⁃条件三元概念，提出了一种基于对象⁃条件三元概念生成三元概念的简便方法.三元背景在经典形式背景（二元背景）上添加条件集，它可以描述在哪些条件下一个对象具有某个属性．一个三元背景由它的每一个非空条件子集可以确定一个二元背景.李俊余等^[14]研究了三元概念和经典形式概念（二元概念）之间的关系，定义了二元概念到三元概念的双射,从二元背景出发描述三元概念，并基于三元概念提出了由每个条件确定的二元背景的二元概念的方法．王霞等^[15]基于三元背景构造了条件属性蕴含形式背景,定义了形式概念、对象定向概念和属性定向概念，并给出了相应的概念格. ...

三元概念的一种构造方法

2019

三元概念与形式概念的关系

2018

三元概念与形式概念的关系

2018

基于条件属性蕴含的概念格构造及简化

2019

基于条件属性蕴含的概念格构造及简化

2019

An information fusion technology for triadic decision contexts

2016

... Tang et al^[16]定义了三元决策形式背景，并基于蕴含规则提出了三元概念的属性约简的定义和方法.该方法使原有的约束决策规则更加紧凑，能更好地对数据进行决策分析，但可能会丢失形式背景中的部分信息.如何将三元因子分析与三元决策形式背景相结合考虑三元概念的简化以及基于可辨识矩阵的三元概念约简的方法与算法设计将是我们进一步要研究的问题. ...

〈

〉

	1						2						3
	1	2	3	4	5	6	1	2	3	4	5	6	1	2	3	4	5	6
1	0	0	1	0	0	0	0	0	1	1	0	0	0	0	1	1	0	0
2	0	1	1	1	0	1	0	1	1	1	0	1	1	1	1	1	0	1
3	1	1	1	1	0	1	1	1	1	1	1	1	0	1	1	1	1	1
4	1	1	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1
5	1	1	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1
6	0	0	1	1	0	1	1	1	1	1	1	1	1	1	1	1	0	1

	1						2						3
	1	2	3	4	5	6	1	2	3	4	5	6	1	2	3	4	5	6
1	0	0	1	0	0	0	0	0	1	1	0	0	0	0	1	1	0	0
2	0	1	1	1	0	1	0	1	1	1	0	1	1	1	1	1	0	1
3	1	1	1	1	0	1	1	1	1	1	1	1	0	1	1	1	1	1
4	1	1	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1
5	1	1	0	1	0	1	1	1	1	1	1	1	1	1	1	1	1	1
6	0	0	1	1	0	1	1	1	1	1	1	1	1	1	1	1	0	1