基于cGAN的下采样LG谱图像优化重建

doi:10.13232/j.cnki.jnju.2023.05.003

基于cGAN的下采样LG谱图像优化重建

叶皓¹^,^*, 王麓懿²^,^*, 吴雪炜^,¹, 张勇²

1.固体微结构物理国家重点实验室，南京大学物理学院，南京，210093

2.南京大学现代工程与应用科学学院，南京，210023

Optimal image reconstruction from down⁃sampled LG spectrum based on cGAN

Ye Hao¹^,^*, Wang Luyi²^,^*, Wu Xuewei^,¹, Zhang Yong²

1.National Laboratory of Solid State Microstructures，School of Physics，Nanjing University，Nanjing，210093，China

2.College of Engineering and Applied Sciences，Nanjing University，Nanjing，210023，China

通讯作者: E⁃mail：wuxuewei@nju.edu.cn

第一联系人: 共同第一作者，

收稿日期: 2023-07-20

基金资助:

中央高校基本业务费. 021314380220
南京大学技术创新基金. 020414913416

Received: 2023-07-20

摘要

对于复杂图像的拉盖尔高斯（Laguerre⁃Gaussian，LG）谱成像，因为满足奈奎斯特采样率的高阶LG模式系数无法测得，重建图像的失真不可避免，而神经网络算法通过先验学习，可以对失真图像实现较为清晰的复原.提出基于条件生成对抗网络（Conditional Generative Adversarial Nets，cGAN）的图像优化重建方法，在处理下采样的LG谱单像素成像和旋转运动模糊图像中均取得了较好的效果.在1.87%的LG谱采样率下，该方法能将Kaggle数据集人像二值图像的结构相似性（Structural Similarity，SSIM）指数提升至0.8以上，和经典图像去噪算法相比有显著提升.

关键词： 频谱下采样 ; 拉盖尔高斯模式 ; cGAN ; 图像优化重建 ; 单像素成像 ; 旋转运动模糊图像复原

Abstract

For Laguerre⁃Gaussian (LG) spectral imaging under Nyquist sampling rate，the reconstructed images are generally distorted because it is difficult to measure the higher⁃order LG mode coefficients. The neural network algorithm can be used to restore these images through prior learning. In this paper，we propose an optimal image reconstruction method based on Conditional Generative Adversarial Nets (cGAN)，which works well in down⁃sampled LG spectral single⁃pixel imaging and rotational motion blur recovery in LG spectral domain. We use the portrait binary images from Kaggle dataset as an example. At a sampling rate of 1.87%，the structural similarity (SSIM) index by using our method reaches 0.8 and above，which is significantly improved comparing with classical image denoising algorithms.

Keywords： spectrum down sampling ; Laguerre⁃Gaussian mode ; cGAN ; optimal image reconstruction ; single⁃pixel imaging ; rotational motion blurred images restoration

PDF (1241KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

叶皓, 王麓懿, 吴雪炜, 张勇. 基于cGAN的下采样LG谱图像优化重建. 南京大学学报（自然科学）[J], 2023, 59(5): 752-758 doi:10.13232/j.cnki.jnju.2023.05.003

Ye Hao, Wang Luyi, Wu Xuewei, Zhang Yong. Optimal image reconstruction from down⁃sampled LG spectrum based on cGAN. Journal of nanjing University[J], 2023, 59(5): 752-758 doi:10.13232/j.cnki.jnju.2023.05.003

图像重建在图像处理领域是一项具有挑战性的热门课题，对图像频率域采样是常见的方法之一，通过频谱滤波得到频率域的每个阶次分量，由此实现对图像全局信息的操控，例如平滑、锐化、去模糊等^［1］.频谱采样率决定图像像素的高低，对高像素数图像或复杂图像的重建，实现频谱完全采样通常较困难，其对探测器要求较高且极其耗时.考虑到低频信息分量占频谱的主要成分，采用牺牲采样率的低通频谱滤波与压缩感知等方法^［2-3］虽然可以重建下采样的图像，但不可避免会造成图像信息较大损失.近年来，深度学习算法因其强大的学习能力和适应性，在图像恢复任务中表现出独特的优势^［4］，与传统模型和算法相比，能从海量数据中通过先验学习到特征训练网络模型，图像处理能力更优异，甚至可以在低采样条件下大幅提高图像重建质量^［5］.

拉盖尔高斯（Laguerre⁃Gaussian，LG）模式是激光谐振器腔内的一种本征模式，在柱坐标下对亥姆赫兹方程做傍轴近似^［6］，其解析解可以表示如下

$L G l, p r, φ = 2 p! π p + l! 1 ω 0 2 r ω 0 l L p l 2 r 2 ω 02 e x p - r 2 ω 02 e x p i l φ = L G l, p r e x p i l φ$ (1)

式（1）为LG光束在传播距离为0处的横向分布，其中l为角向指数，取任意整数；p为径向指数，取大于0的整数； $L_{p}^{|l|}$ 为拉盖尔多项式； $ω_{0}$ 为束腰半径.可将LG光束描述为径向分布 $L G_{l, p} (r)$ 与角向分布 $e x p (i l φ)$ 之积，其中角向指数l与径向指数p的任意组合形成不同的LG模式，所有LG模式构成一组完备正交基底.傅里叶基底构成的变换域为图像频谱，而相应LG基底构成的变换域为图像LG谱^［7］.LG谱采样是一种频谱采样手段，具有较高的采样效率.此外，由于LG模式具有的圆对称横向空间分布，在空间上具有旋转不变的特性^［8］，其在角向探测方面具有独特优势，广泛应用于小角度测量、对称性物体识别、动态旋转物体成像等领域^［9］.

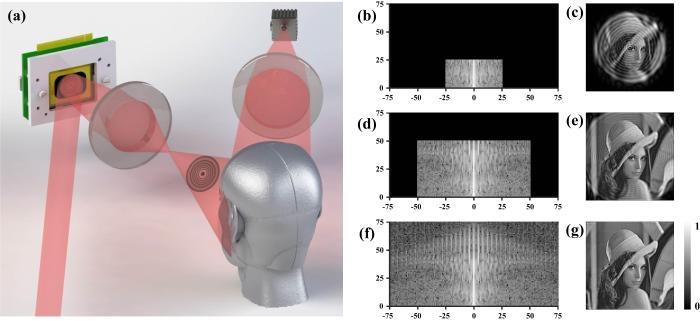
在单像素成像过程，通过投影一定数量的LG模式，可得到图像的下采样LG谱^［10］.如图1a所示，入射光经过一台数字微镜（DMD），其具有像素级编码与高帧率刷新功能，用于加载并切换产生LG模式的全息图.产生的LG模式经过透镜成像系统投影至目标物体，目标物体的反射光经聚焦透镜汇聚并由一台单点探测器采集.单点探测器采集到的信号强度可以表示为：

$I = ∑ l ∑ p U r, φ L G l, p r c o s φ l + θ$ (2)

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 LG谱采样的单像素成像系统（a）；不同的LG模式截止阶数及其对应的重建图像：(b~c) l₂₅p₂₅，(d~e) l₅₀p₅₀和(f~g) l₇₅p₇₅

Fig.1 Single⁃pixel imaging system of LG spectrum sampling (a)，different ranges of LG spectrum and the reconstructed images：(b~c) l₂₅p₂₅，(d~e) l₅₀p₅₀ and (f~g) l₇₅p₇₅

其中， $U (r, φ)$ 为目标物光场分布， $θ$ 为LG模式的附加相移.当相移 $θ$ 分别取值 $0, π / 2, π, 3 π / 2$ 时，构成图像的某一阶次LG谱模式系数 $A_{l, p}$

$I 0 - I π + i I 3 π / 2 - I π / 2 = ∑ l ∑ p U r, φ L G l, p r c o s l φ + i s i n l φ = ∑ l ∑ p U r, φ L G l, p r e x p i l φ = A l, p$ (3)

通过数字微镜器件（Digital Micromirror Devices，DMD）切换大量不同的LG模式，即可计算得到物像的LG谱.图1b，1d和1f是截止阶数分别为25，50和75的下采样LG谱，其中横坐标为角向指数l，纵坐标为径向指数p，图1c，1e和1g分别为对应的重建图像.由图可见，当采样率较低、LG模式截止阶数较小时，重建图像的视场较小，清晰度较差，随着截止阶数的增大，重建图像的细节恢复变好，图像噪声也变弱.并且，由于LG模式具有独特的径向参量，截止阶数较小，重建图像在径向具有明显的噪声.因此，在低采样率下提升单像素LG谱下采样的成像质量具有实际的研究价值.

此外，当相机拍摄高速旋转的物体时，由于相机的响应速度有限，拍摄的图像会有一定的旋转运动模糊.把高速旋转物体在某一时刻t的光场表示为

$U t r, φ, t = ∑ l ∑ p A l, p L G l, p r e x p i l φ e x p i l ∫ 0 t Ω τ d τ$ (4)

其中， $Ω (τ)$ 为物体在任意时刻的转速.相机快门控制的曝光时间为T，则最终拍摄得到的图像为物体的光场分布在曝光时间内的积分，即

$U b r, φ = ∫ 0 T U t r, φ, t d T = ∑ l ∑ p ∫ 0 T e x p i l ∫ 0 t Ω τ d τ d t ⋅ A l, p L G l, p r e x p i l φ$ (5)

可见，相机拍摄得到的旋转模糊图像由物体的转速和相机的曝光时间决定.在匀转速时，曝光时间与物体旋转角频率之积为物体在相机曝光时间内的旋转模糊角度.图2a为静止原图像，图2b~d分别为5°，15°和25°时的旋转模糊角度图像.由图可见，随着旋转模糊角度的增大，图像的不同空间位置混叠导致的失真越来越明显，在远离中心位置处的图像信息尤甚.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 静止原图(a)和旋转运动模糊图像，模糊角分别为5° （b），15° (c)和25° (d)

Fig.2 The original image (a) and the rotational motion blurred images with blurred angles of 5° (b)，15° (c) and 25° （d）

针对上述LG模式下采样单像素成像与旋转模糊成像过程中的问题，应用条件生成对抗网络（Conditional Generative Adversarial Nets，cGAN）模型来重建失真图像.对Kaggle人像数据集^［11］在1.87%的LG谱采样率下，下采样单像素成像的结构相似性（Structural Similarity，SSIM）指数的平均值由约0.55提升至约0.88，旋转模糊成像的SSIM指数的平均值由约0.30提升至约0.84，和中值滤波（Median Filtering，MF）^［12］、非局部均值滤波（Non⁃Local Means，NLM）^［13］与降噪自编码器（Denoising Autoencoder，DAE）^［14］算法相比，重建图像质量得到了显著优化.

1 研究方法

利用cGAN对LG谱下采样恢复的图像进行优化重建.近年来，生成对抗网络（GAN）方法已占据主导地位^［15-16］，其通过生成器和鉴别器的相互对抗学习，将随机噪声拟合为原始图像的分布^［17］，但经典GAN常出现结果无法收敛的问题，训练时不稳定^［18］.cGAN在GAN的基础上加入条件概率分布的信息，有利于数据增强^［19］，让生成的模型更容易受控^［20-21］.

cGAN模型是原始GAN的拓展模型，原始GAN的目标函数可以表示为^［15］：

\begin{array}{l} \underset{G}{m i n} \underset{D}{m a x} V (D, G) = E_{x ~ P_{d a t a} (x)} [l g D (x)] + \\ E_{z ~ P_{z} (z)} [l g (1 - D (G (z)))] \end{array}

(6)

其中，G代表生成器，D代表判别器，z代表分布为 $P_{z}$ 的随机噪声，x代表分布为 $P_{d a t a}$ 的目标数据.cGAN的目标函数可以表示为^［20］ $\begin{array}{l} \underset{G}{m i n} \underset{D}{m a x} V (D, G) = E_{x ~ P_{d a t a} (x)} [l g D (x| y)] + \\ E_{z ~ P_{z} (z)} [l g (1 - D (G (z| y)))] \end{array}$ (7)

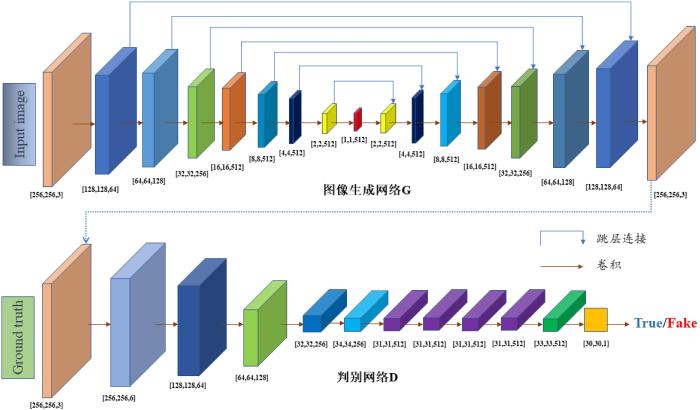
与式（6）不同的是，式（7）多了一项y，代表条件信息.其中，G试图最小化 $V (D, G)$ ，而D则试图最大化 $V (D, G)$ ，最后两者在相互博弈中达到纳什均衡，此时认为生成器生成的图像就是需要的目标图像.

cGAN的生成器基于U⁃Net结构，由编码器和解码器组成，结构如图3所示.编码器用一系列卷积动作连续下采样来提取特征，在此过程中信息被压缩了.解码器进行的是反卷积动作，需要对原本较少的信息进行扩充，在此过程中空间信息丢失，难免出现类似求解欠定方程的情形，不能得到精确解.因此U⁃Net网络通过跳跃连接将编码器相同结构的层作为输入连接到解码器，补偿下采样过程中的信息损失.cGAN的判别器为卷积神经网络（Convolutional Neural Networks，CNN），将生成图像和真实图像拼接成的图像对作为判别器的输入，判别器不断对图像进行卷积和池化操作，最终得到判别器认为生成图像是真实图像的概率.若判别器认为生成图像为真实图像则输出1，虚假图像则输出0.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 cGAN模型的结构图

Fig.3 The structure of cGAN model

利用Kaggle平台的公开人像数据集来进行实验.为了减少LG模式的分解和逆变换的计算量，预先对其进行二值化处理，使用插值算法将图像尺寸调整至256×256并对这些图像进行LG模式的分解和逆变换重建.随机抽取1200张逆变换的图像作为训练集，剩余的图像为测试集.在神经网络的训练过程中，将选取的图像尺寸扩大至286×286并随机裁剪，以提高算法的鲁棒性.在TensorFlow平台上进行网络训练，训练过程单次传递用来训练的样本数为1，利用Adam算法^［22］计算梯度，学习率设为0.002，动量值设为0.5，最终得到训练好的网络.

2 实验与结果

分别将LG变换的下采样单像素成像图像和旋转运动模糊图像的LG变换的下采样图像输入已训练好的网络进行测试，使用的LG模式范围为 $l_{0} p_{0} ~ l_{34} p_{34}$ ，共1225个模式，图像大小为256×256，则此时采样率仅为1.87%.重建图像与原图真值对比，以SSIM作为评价标准，从亮度、对比度和结构三个方面判断两张图片的相似性，范围为0~1，数值越大，重建效果越好.

对于测试的失真图像，使用较有代表性的图像去噪声算法处理进行对比，包括MF，NLM和DAE.MF是一种局部滤波方法，选取图像数字矩阵中相邻的奇数个像素点数值的中间值替代原来的像素值，以此来消除噪声点.NLM理论上可以在整个图像中计算像素的相似度，考虑效率问题，也可以设置一个相对较大的搜索窗口和一个相对较小的邻域窗口，根据邻域间的相似度确定具体的像素值.DAE是一种无监督的学习方法，可通过训练数据的自编码器来学习信号的特征^［23-24］，然后再使用这些特征去除噪声.

图4为测试集部分人像图像的LG谱下采样的MF，NLM，DAE，cGAN方法重建效果的对比图.从LG变换后的下采样图像可以看出，因截止阶数较小，欠采样率较大，LG模式重建图像的径向噪声较明显.虽然以往的工作证明MF算法在对抗椒盐噪声的场景下有较好的效果，但对全局都存在的背景噪声几乎不起作用；NLM算法虽然能对整个图像进行滤波，但对全图大范围存在的背景噪声缺乏识别能力，只能将背景噪声平均分配到整张图像中；DAE算法的表现优于滤波算法，但整体降噪效果逊色于cGAN.图5还展示了对15°旋转模糊角度的LG谱下采样的人像图像重建效果对比.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 人像图像LG谱下采样条件下使用MF，NLM，DAE和cGAN算法的重建效果

Fig.4 Images reconstructed by MF，NLM，DAE and cGAN with LG spectrum down⁃sampling

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 15°旋转模糊人像图像在LG谱下采样条件下使用MF，NLM，DAE，cGAN算法的重建效果

Fig.5 Images reconstructed by MF，NLM，DAE and cGAN with LG spectrum down⁃sampling of 15° rotational motion blurred images

表1与表2分别列出了不同处理方法处理常规和15°旋转模糊的人像图像对应的SSIM.由表可见，和其他三种算法相比，cGAN生成的图像与真实图像之间的SSIM较高.和常规人像图像相比，15°旋转模糊的人像图像经过LG变换后的下采样图像的SSIM更低，仅为0.3左右，但由cGAN重建后的图像的SSIM均达到0.8以上.

表1 人像图像LG谱下采样的MF，NLM，DAE，cGAN方法重建图像的SSIM

Table 1 SSIM of images reconstructed by MF，NLM，DAE and cGAN with LG spectrum down⁃sampling

图号	LG变换	MF	NLM	DAE	cGAN
4a	0.434	0.454	0.548	0.654	0.841
4b	0.636	0.653	0.765	0.850	0.932
4c	0.613	0.631	0.767	0.726	0.886
4d	0.536	0.554	0.674	0.738	0.868
4e	0.544	0.561	0.673	0.759	0.884

新窗口打开| 下载CSV

表2 15°旋转模糊人像图像LG谱下采样的MF，NLM，DAE，cGAN方法重建图像的SSIM

Table 2 SSIM of images reconstructed by MF，NLM，DAE and cGAN methods with LG spectrum down⁃sampling of 15° rotational motion blurred images

图号	LG变换	MF	NLM	DAE	cGAN
5a	0.301	0.307	0.371	0.511	0.825
5b	0.263	0.269	0.337	0.479	0.858
5c	0.307	0.313	0.366	0.508	0.822
5d	0.272	0.279	0.349	0.530	0.834
5e	0.331	0.338	0.410	0.585	0.866

新窗口打开| 下载CSV

MF与NLM算法，重建每张图片的运算时间短于0.02 s；DAE算法以及本文提出的基于cGAN的图像重建算法，将网络模型训练好之后，重建每张图像的运算时间短于0.1 s.

综上，基于cGAN的图像重建方法，在LG谱的低采样率情形下表现出较强的图像恢复能力，并且对旋转模糊图像有较好的重建效果，鲁棒性也较强.

3 结论

本文提出一种基于条件生成对抗网络的LG谱图像重建方法，通过生成器与鉴别器的相互对抗学习，将输入的失真图像拟合为与原图相似度较高的图像.研究证明，在LG谱的低采样率情形下，本文提出的算法实现了与原图结构相似度较高的图像重建，优于经典的图像去噪声算法.此外，在相同采样率下，该方法对旋转模糊图像同样具有较好的重建效果，鲁棒性较强.该方法在下采样LG谱成像过程中明显提升了图像重建精度，为单像素成像、模糊图像复原提供了一个可行的方案.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Gonzalez

R C

， Woods

R E

. 数字图像处理. 阮秋琦，阮宇智译. 北京：电子工业出版社，2017：169-186.