低空航拍全景图像拼接研究

doi:10.13232/j.cnki.jnju.2023.02.006

低空航拍全景图像拼接研究

代家印, 王育昕^,, 袁杰

南京大学电子科学与工程学院，南京，210023

Research on low⁃altitude aerial panoramic image stitching

Dai Jiayin, Wang Yuxin^,, Yuan Jie

School of Electronic Science and Engineering，Nanjing University，Nanjing，210023，China

通讯作者: E⁃mail：wyx@nju.edu.cn

收稿日期: 2022-11-02

基金资助:

江苏省自然科学基金. BK20181280

Received: 2022-11-02

摘要

航拍图主要被用来作为一些图像处理的基础材料，但是由于无人机飞行高度的自限性和一些干扰因素导致图像的视野和对齐效果受限，致力于研究一种改良的对齐评估方法和运动目标去除以提升全景拼接的效果，以减少局部扭曲，使得拼接结果更加接近自然和平滑.采用网格优化引导拼接来提升全局拼接效果，对于网格的规划采用三个联合的能量函数进行求优，对齐效果的直观感受来源于人类视觉对场景目标中的边缘和线条对齐的观察.因此，加入直线对齐能量函数作为联合的优化方法也能在一定程度上提高对齐的效果，拼接角度问题通过估计一个合适的三维旋转来缓解.最后，对于场景中的动态目标的影响，使用深度学习中的实例分割网络进行潜在的运动目标去除，比如行人、车辆等，并在分割网络输出的目标区域进行图像修复.

关键词： 全景拼接 ; 网格优化 ; 实例分割 ; 自然性

Abstract

Aerial photos are used as the basic material for some image processing. However，due to the self⁃limitation of the drone's flying height and some interference factors，the field of view and alignment of the image aren't good. This paper is devoted to studying an improved alignment evaluation method and moving target removal to improve the effect of panoramic stitching，reduce distortion，and make the stitching more natural and smooth. Here，grid optimization is used to guide stitching to improve the global stitching，for this method，three joint energy functions are used for optimization. The intuitive feeling of the alignment effect comes from the human vision's observation of the edge and line alignment in the scene，therefore，adding the linear alignment energy function as a joint optimization method can improve the alignment effect to a certain extent. And the angle problem is alleviated by estimating a suitable 3D rotation. Finally，for the impact of dynamic objects in the scene，this paper uses the instance segmentation network in deep learning to remove potential moving objects，such as pedestrians，vehicles，etc.，and performs image inpainting in the target area output by the segmentation network.

Keywords： panoramic Stitching ; grid optimization ; instance segmentation ; naturalness

PDF (1016KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

代家印, 王育昕, 袁杰. 低空航拍全景图像拼接研究. 南京大学学报（自然科学）[J], 2023, 59(2): 239-246 doi:10.13232/j.cnki.jnju.2023.02.006

Dai Jiayin, Wang Yuxin, Yuan Jie. Research on low⁃altitude aerial panoramic image stitching. Journal of nanjing University[J], 2023, 59(2): 239-246 doi:10.13232/j.cnki.jnju.2023.02.006

图像拼接是一种计算机视觉处理任务的基础任务，在获取更大的景观视野及城市规划任务中具有一定的应用价值，拼接在算法层面上降低了对高级的硬件需求.拼接的方法有基于传统的和近年来火热的深度学习方法，目的是提高图像的对齐效果，尽可能减少扭曲^［1］.传统的方法一般是基于单应性变换，基于单应可逆性将一组图片进行传递拼接到一个完整的画布.但是单应估计在很大程度上依赖图像的配准工作，配准工作在特征点和特征描述子方面有很多不确定性导致估计结果的不稳定，比如漏拼、对齐质量差.

漏拼问题常见于拼接图像对无法获取一个数量足够的匹配点对用于配准而被舍弃，这严重违背了拼接的基本准则，即保留原有图像信息.配准不仅仅对检测算子的建模要求高，更对场景的纹理丰富度提出了一定的要求，重复纹理、缺失纹理、遮挡问题都对特征匹配提出了挑战^［2］.为了解决纹理的问题，人们设计了很多复杂的模型用于检测，模型的复杂化势必会牺牲效率.1988年，经典的Harris角点检测算法横空出世，将图像中具有旋转、平移不变性的角点作为特征点进行图像配准.1999年，加拿大英属哥伦比亚大学教授Lowe提出了SIFT （Scale⁃Invariant Feature Transform）算法，进一步提升尺度不变特征变换，并在2004年将其完善^［3］.由于SIFT的检测效率太低，后人在此基础上衍生了比较快速的SURF （Speeded⁃Up Robust Features）算法^［4］.更有后来者将不同的特征点检测算子和描述子进行结合在保证精确度的情况下提升检测的效率，比如ORB （ORiented Brief）算法^［5］.尽管如此，在低纹理的情况下，无法保证图像配准的质量.所以对于特征点的使用，只能作为一个初始的配准，不能仅仅依靠特征点.

另外，拼接算法基于两个重要的假设：（1）相机光心一致假设；（2）拍摄纯平面假设^［6］.然而，在现实的拍摄场景中，无法保证这两个拍摄条件的成立.非平面情况下物体的景深不一致使得局部的尺度因子不具备统一性，所以导致在图像中估计一个全局的单应关系难以用于各个局部的对齐.在对传统的单应估计方法的改进中，很多前人的研究开始转向多个单应矩阵联合拼接，这是一个启发式的开端.在2011年的CVPR会议上DHW （Dual⁃Homography Warping）算法开始将场景划分为前景和背景两个平面，然后分别对齐前景和背景，在大部分场景中可以实现完美的无缝拼接^［7］.分块优化算法中具有代表性的里程碑算法有APAP （As⁃Projective⁃As⁃Possible），此方法是将单个图像分割为比较密集的网格块，然后各个网格都计算一个与之对应的单应矩阵用于网格内的对齐，我们称之为局部单应性^［8］.

在对拼接优化的研究中，网格规划是一个行之有效的方案，既然估计一个全局的单应矩阵无法满足拼接的需求，那么对图像进行分块处理进而对每个区域进行单应映射可以缓解局部不对齐的问题.在2014年的CVPR会议上提出的SPHP （Shape⁃Preserving Half⁃Projective）算法从校正形状的方向借鉴图像缩放的方法图像非重叠区域逐渐过渡到全局相似性变换，并对整个图像的相似性进行约束，减小了投影的失真^［9］.2015年CVPR提出了AANA （Adaptive As⁃Natural⁃As⁃Possible）算法，同样也是对形状进行校正，采用全局相似项约束，拼接的结果观感自然度比SPHP提升了一个档次^［10］.APAP算法是一个比较成功的案例，是以上改进方法的基础.受此启发，本文提出了一种基于网格优化的全自动的低空航拍图像拼接，利用SIFT特征点对作为图像配准的初始化点，然后通过APAP对齐的方法将网格的对齐顶点作为我们对齐函数的优化对象，算法的核心思想是找到一组变形后的顶点，通过变形前后的顶点对齐能量函数最小化来确定变形后的顶点位置^［11］.最后通过这些优化过的顶点作为局部的单应估计点对达到网格级别的对齐，同时在优化函数里添加了对直线的失真评估来确定一个合适的3D旋转角度使得拼接的结果视角更加的自然.为了消除动态目标在网格中的影响，本文使用了实例分割网络进行了潜在运动目标检测分割任务，以获取目标的掩模而进行区域的修复缓解由于场景中相对运动带来的扭曲问题.现存的比较成功的传统拼接方法有AutoStitch，APAP等，通过上述方法和本文方法在组图的漏拼比、拼接效率和直线的对齐程度等参数来说明本文方法的先进性.另外，本文对方法的局限性也进行了讨论.

1 基于网格对齐的拼接优化方法

1.1　匹配图生成

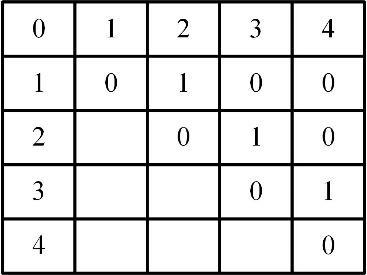
拼接自动化是低空航拍拼接的关键前提，算法首先保证拼接是一个没有人为参与的过程，对于拼接而言我们不应该对空间时间提出特定要求，那么在一个自由的空间中获取的图片组的拼接连接关系需要一个匹配图矩阵来引导拼接顺序.对于匹配图的定义，首先对获取的图像组分配序号（0，1，2，3，…），然后约定一个二维矩阵的行列标号分别为对应的图片序号，行列索引代表了两个指定图像，该索引位置下的元素使用布尔变量表示匹配关系的存在与否.矩阵定义如图1所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 匹配图

Fig.1 Matching graphy

观察上述矩阵，可以发现它是一个上三角阵，这也意味着我们的图片遍历顺序是严格正序的.对于匹配关系的确定，本文使用了特征匹配点数作为依据，点数和图像分辨率之比可以确定两个图像是否有一个邻接关系.为了方便快捷地完成这个预处理任务，本文使用了SURF特征匹配算法的CUDA（并行计算单元）加速版本^［12］.匹配图中会随机生成一个拼接图像中心，剩余图像通过匹配图完成到中心的拼接，所以匹配图需要一个有效性验证来保证所有图像最终被拼接在同个画布上，同时需要剪枝操作以避免不必要的邻接关系来减少图像之间的耦合性，降低优化复杂度并节省拼接时间.

对于匹配图的有效性验证.首先准备一个线性容器，大小为图片的总数量，用于标志图片是否被拼接在画布上.最后的验证是当该容器里布尔变量真值个数与图片数量一致时，验证通过.具体的该容器的布尔变量定义规则为：第一步，在所有的图片序号中随机选出一个拼接中心，使用图片的序号作为线性容器的下标进行容器访问，并定义该位置的布尔值为真；第二步，借助一个队列进行协同操作，将拼接中心序号入队列；第三步，开始使用迭代算法，迭代访问队列中的内容，每迭代一次（即出队列访问一次）将队列头与其他所有的图片序号进行两两配对作为匹配图二维矩阵的下标进行访问，这一步实际就是在匹配图中遍历与当前队列头图片序号相邻接的图像序号，对应的线性容器位置修改值为真，并入队列；第四步迭代结束，验证真值的个数是否与容器的大小相同.剪枝操作，对于同行同列的元素，在保证构成连通域和有效性的前提下，只保留一个真值布尔变量即可，不失一般性的同一行中所在列数数值小的匹配关系可以置零，同一列中所在行数高的可以置零.此操作既可以保证拼接图是完整的避免漏拼现象又可以减少不必要的拼接次数以提高拼接效率，并在一定程度下还能减少局部扭曲程度.因为缝合的次数越多扭曲越容易发生，这里使用了全局平滑项.单个图像的拼接邻接图越多，受到全局能量函数的影响越大，更易产生局部扭曲.

1.2　匹配点生成

特征点由于纹理分布的不确定和各种不稳定因素的干扰对于估计单应矩阵而言是十分不友好的.所以本文用生成的匹配点来代替特征点，匹配点是基于网格的划分，也就是网格的顶点，相比于特征点拥有更加均匀的分布.假设对两幅图像A，B进行网格划分，然后使用APAP方法进行对齐，并将之作为初始对齐点，然后使用顶点对齐能量函数进行优化，获得最终的对齐点，即匹配点.在完成对特征点的检测和匹配点的生成之前，首先将图像集编号为 $I_{i} (i = 0,1, 2,3, \dots)$ ，并设 $J$ 是一组拼接的图像对，对于 $J$ 中的 $I_{i}$ 和 $I_{j}$ ，利用APAP来使之对齐.在两个对齐图像重叠区域中对 $I_{i}$ 的网格顶点进行检测并设定为匹配点集合，并记作 $M^{i j}$ ，对于集合 $M^{i j}$ 中的每个匹配点，在 $I_{j}$ 中都有唯一的点与之对应，因为 $I_{i}$ 和 $I_{j}$ 已经确定了对齐关系，所以设定 $M^{j i}$ 表示 $I_{j}$ 在 $I_{i}$ 中的匹配点集合，这表示对称可逆关系，可以通过重投影进行误差验证，而目标函数通过计算对齐点的相关函数能量误差来优化匹配点.特征点和通过函数优化对齐之后的匹配点如图2所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 特征点和匹配点

Fig.2 Feature points & matching points

1.3　顶点对齐目标函数

网格的顶点在完成APAP的对齐之后需要进行优化以达到更加优良的对齐效果，优化试图找到一组顶点使得对应的目标函数最小化.目标函数包括顶点对齐误差，局部相似性变换和全局相似性变换.对于拼接图像我们设定每个对象 $I_{i}$ 中的网格顶点为 $V_{i}$ ，网格边为 $E_{i}$ ，那么所有图像的顶点集合为 $V$ ，所有边的集合为 $E$ ，变形后的顶点设为 $\tilde{V}$ .拼接结果的评价标准不同，对于目标函数的设计就不同，本文的目的是使拼接图像更加的平滑、减少局部扭曲、提升一定的自然性^［10］.自然性是人类视觉的直观感受，取决于图像的拼接视角缩放系数和整体的拼接变换相似性.我们尽量保留图像原有的角度，并使得局部乃至全局的变换是相似的，不至于产生较大的扭曲.首先关注函数的对齐项，顾名思义对齐项是对变形顶点前后的位置的误差做出最小化约束.其定义如式（1）所示：

W_{a} (v) = \sum_{i = 1}^{N} \sum_{(i, j \in J)} \sum_{p_{k}^{i j} \in M^{i j}} {‖\tilde{v} (p_{k}^{i j}) - \tilde{v} (φ (p_{k}^{i j}))‖}^{2}

(1)

其中， $φ (p)$ 是网格中对齐点 $p$ 的对应关系点，即上式计算的是对齐前后的点的误差能量函数.函数 $\tilde{v} (p)$ 是4个顶点的线性组合用来表示顶点 $p$ ， $\tilde{v} (p) = \sum_{i = 1}^{4} α_{i} {\tilde{v}}_{i}$ ， ${\tilde{v}}_{i}$ 表示 $p$ 所在的网格的4个角坐标，而 $α_{i}$ 是顶点 $p$ 的双线性权值.局部相似相 $W_{l}$ ，此项函数是用于正则化约束防止局部变形过大，还有一个重要作用是将对齐项约束从重叠区域逐渐传播到非重叠邻域，这样来实现局部的一致性们对这个函数的优化是为了确保每个网格都能进行对应的相似变换.具体定义如式（2）所示：

W_{l} (v) = \sum_{i = 1}^{N} \sum_{(j, k \in E_{i})} {‖({\tilde{v}}_{k}^{i} - {\tilde{v}}_{j}^{i}) - s_{j k}^{i} (v_{k}^{i} - v_{j}^{i})‖}^{2}

(2)

其中， $v_{j}^{i}$ 是变形前网格顶点的位置， ${\tilde{v}}_{j}^{i}$ 是拼接图经过变形后的网格顶点的位置， $s_{j k}^{i}$ 是对应边 $(j, k)$ 的相似变换，可以被定义为式（3）所示：

s_{j k}^{i} = [\begin{matrix} c (e_{j k}^{i}) & s (e_{j k}^{i}) \\ - s (e_{j k}^{i}) & c (e_{j k}^{i}) \end{matrix}]

(3)

其中，系数 $c (e_{j k}^{i})$ ， $s (e_{j k}^{i})$ 表示顶点变量的线性组合^［13］.全局相似项 $W_{g}$ ，此优化项在确保每个图像的边能大概率进行同样地变换中扮演着重要角色，相似的变换操作对于提高图像拼接整体的自然性尤为重要，如果不对整体变形限以约束，变形可能出现歪斜或者非均匀形变导致扭曲，而且它在一定程度上解决了 $v_{j}^{i} = 0$ 的一般解.如果已经选择好了图像 $I_{i}$ 合适的缩放比例 $s_{i}$ 和旋转角 $θ_{i}$ 后，全局相似性定义为式（4）所示：

W_{g} (V) = \sum_{i = 1}^{N} \sum_{e_{j}^{i} \in E_{i}} w {(e_{j}^{i})}^{2} [{(c (e_{j}^{i}) - s_{i} c o s (θ_{i}))}^{2} + {(s (e_{j}^{i}) - s_{i} s i n (θ_{i}))}^{2}]

(4)

这里的适当的缩放比例和旋转的获取方法将随后会详细叙述.上式表明需要为每个图像 $I_{i}$ 的每个边 $e_{j}^{i}$ 进行一个对应的相似变换，与为图像做相似变换有同步的操作，而函数 $c (e)$ 和 $s (e)$ 等式的值与式（3）所述的输入边 $e$ 的相似变换的系数的获取方式相同.重叠区域的边界邻域需要权重进行对齐校正，此时使用的是权重函数 $w (e_{j}^{i})$ 修正重叠区域的四边形的对齐效果，非重叠区域由于没有对齐约束，那么对距离重叠区域较远的边界区域使用一些先验相似项^［14］，权重定义则依赖先验准则，如式（5）所示：

w (e_{j}^{i}) = β + \frac{γ}{|Q (e_{j}^{i})|} \sum_{q_{k} \in Q (e_{j}^{i})} \frac{d (q_{k}, M^{i})}{\sqrt[]{R_{i}^{2} + C_{i}^{2}}}

(5)

其中， $β, γ$ 是权重系数常数，由实验经验给出； $Q (e_{j}^{i})$ 是公共边 $e_{j}^{i}$ 的四边形组合（1~2个四边形，具体的取决于公共边是否在划分网格的边界上）；函数 $d (q_{k}, M^{i})$ 是四边形 $q_{k}$ 到网络空间重叠区域的四边形的距离， $M^{i}$ 是表示 $I_{i}$ 重叠区域的四边形集合； $R_{i}$ 和 $C_{i}$ 分别代表了图像 $I_{i}$ 中网格的列数和行数.简而言之，原则是非重叠区域的权重与其边缘到网格空间中重叠区域的归一化距离成一定比例关系.网格的最终变形通过以下总体约束来达到最佳，如式（6）所示：

\tilde{V} = \underset{\tilde{V}}{a r g m i n} φ_{a} (V) + λ_{l} φ_{l} (V) + φ_{g} (V)

(6)

需要注意的是全局相似性函数 $W_{g}$ 中有 $β, γ$ 两个常量参数，这对控制全局相似项有着至关重要的作用.实验中设定 $λ_{l} = 0.56$ ， $β = 6$ ， $γ = 20$ .这是根据实验结果得出的比较稳定的参数值，保证各优化项之间能够有一个良好的均衡性，而上述优化问题则可以通过使用稀疏线性优化器进行求解^［15］.

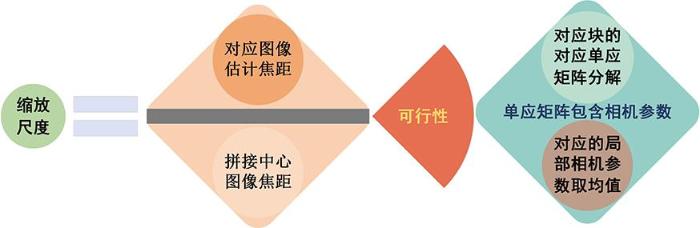
全局相似项使用了合适的尺度因子和旋转角度，对于这两个参数的估计主要是通过单应矩阵的分解来实现^［16-18］.可行性如图3所示.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 确定缩放尺度

Fig.3 Scale factor

本文对APAP对齐后的网格使用了局部单应性求解，并对结果进行分解得到初始化的相机内参 $K_{i}$ ，相机内参与中心图像内参之比可确定缩放因子.在获取了相机内参后可以通过最小化重投影误差来估计一个旋转矩阵，如式（7）所示：

R_{i j} = \underset{R}{a r g m i n} \sum_{p_{k}^{i j} \in M^{i j}} {‖K_{j} R K_{i}^{- 1} p_{k}^{i j} - φ (p_{k}^{i j})‖}^{2}

(7)

此优化项通过SVD（矩阵奇异值）分解来实现求解^［19］.这里讨论一个重点的优化项最小化直线失真，即用于直线的对齐评估.每两幅图像之间的每对匹配点可以确定一个相对旋转角度，因此在两幅图像的点集中确定的角度集中限定了我们估计的角度的旋转范围，作为最小化直线失真估计角度的合理范围.最小化直线失真如式（8），定义包含了两个部分，第一部分是直线对齐失真的旋转估计，第二部分是图像匹配点的旋转估计.

\begin{array}{l} \sum_{(i, j) \in Ω} {‖R (\emptyset^{i j}) [\begin{matrix} u_{i} \\ v_{i} \end{matrix}] - [\begin{matrix} u_{j} \\ v_{j} \end{matrix}]‖}^{2} + \\ λ_{γ} \sum_{(i, j ϵ \tilde{Ω})} {‖R (α^{i j}) [\begin{matrix} u_{i} \\ v_{i} \end{matrix}] - [\begin{matrix} u_{j} \\ v_{j} \end{matrix}]‖}^{2} \end{array}

(8)

其中， $\emptyset^{i j}$ 是二维旋转角度，是每对直线确定的相对旋转角的均值， $α^{i j}$ 是三维旋转角，是匹配点对重投影误差估计的旋转矩阵 $R_{i j}$ 绕图像三维左手坐标系的z轴分解而来.

1.4　动态目标去除

动态目标的运动检测一直是一个重要的研究课题，传统的检测方法大多是对模板和光流的匹配，效果并不理想.事实上，运动目标一般是一些常见的可移动物体也称为潜在运动目标，包括行人、车辆等，而对于航拍图而言，行人的占比可忽略不计，所以重点检测出移动的车辆就可以做出相对的影响消除.由于航拍不是定点拍摄，导致设备和场景同时发生了运动，基于传统的模板匹配已经很难适应这种场景，所以本文使用了深度学习中的实例分割网络Mask⁃RCNN进行了潜在运动目标的检测^［20］.Mask⁃RCNN在Faster⁃RCNN的基础上用ROI⁃Align（双线性插值）取缔了ROI⁃Pooling（池化），并在主干网络提取的特征图上添加了一个二维的交叉损失熵回归用于像素级的分类实现实例分割.我们对无人机航拍数据集Drove进行了标注和标签的制作，用于训练网络，并迁移到低空航拍数据集中进行网络微调（Fine Tune）.经过训练之后的网络可以对航拍图中的车辆物体实施较为精确的分割从而获得一个掩模区域，掩模对于修复该区域十分重要.修复基于快速行进算法^［21］，首先从区域的边界开始，随后进入区域内，逐渐使用邻域像素填充边界中的像素.像素由邻域中所有已知像素的归一化加权和计算.权重的确定是一个重点项，对于靠近需要修复的像素集，靠近边界的法线和位于边界轮廓上的像素，给予更多的权重.

2 实验与结果

实验使用的航拍设备是大疆无人机（DJI AIR 2S），相机分辨率为5472×3648，取景地点为校园操场和道路，飞行高度为100 m.本文采用平移飞行和环绕飞行两种方式各10组拼接数据且具备移动车辆测试组，一组拼接图像数量为四.分割网络采用的是集成了Mask⁃RCNN的detectron2计算机视觉库，其来自Facebook AI团队，支持实例分割.拼接平台使用NVIDIA TX2可移动高性能嵌入式平台，该平台整合了四核ARM A57 CPU、Pascal架构GPU （16 nm工艺并行计算架构）、最高8 G内存、32 G固态存储器等组件，标准功耗为7.5 W.该平台可以在无人机的搭载下实现一体化低空航拍系统，运行效率高且稳定.

首先对实例分割网络进行预训练.预训练模型基于COCO （Common Objects in Context）^［22］，然后对无人机飞行数据集106张图片执行300轮训练，训练集包括五个类别（道路、植被、车辆、房顶、建筑物正面），选择的场景基于航拍图像的一般场景类别，而COCO作为图像处理领域的大规模数据集包含了150万个目标，80个目标类别（包括行人和车辆），91个材料类别.这对于预训练一个自然场景特征提取能力强的主干网络而言是非常有效的.初始学习率设定为0.002，在每十轮后进行一个学习率的衰减，以稳定的收敛.最后使用拼接数据集进行微调训练，以网络最佳适应我们的应用场景.本文所关注的是网络对潜在运动目标车辆的识别和分割能力，通过测试验证了我们的车辆分割和手工车辆分割的交并比平均达到86.34%，满足对车辆区域的提取任务.

对于我们的实验而言，我们的网络模型已经可以获取一个稳定可靠的动态目标掩模，足够提供支持对掩模内容进行修复，以下分别对动态目标的有无使用本文描述的算法执行拼接，其结果如图4所示.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 实例分割结果（左：分割前；右：分割后）

Fig.4 Instance segmentation (left: before,right: after)

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 动态目标影响（左：有目标，右：无目标）

Fig.5 Vehicle impact comparison,with (left) and without (right) target

实例分割的结果中由于精度的问题导致除了车辆被检测出，还附着了很多不需要关注的物体框，然而这些多余的目标框对图像修复任务并不存在干扰，只有类别为车辆的框内分割区域才会被我们的算法所修复.不难发现拼接后的上示全景图中，黑色轿车并没有对齐且出现了错位，道路也没有完全的对齐，图像的边缘出现了扭曲现象.但是在经过掩模处理后，主要是为了消除可能会移动的车辆，去除有位移的车后，发现对齐的结果明显提升，且扭曲程度大大降低，每张图像形变程度并不高且基本保留了原有的姿态.通过量化的拼接完整度、效率和扭曲度三个参数来说明算法的提升效果（表1）.

表1 参数对比

Table 1 Comparison of performance parameters

方法	漏拼比	拼接时间	直线扭曲度
AutoStitch	10.23%	22.39 ms	4.91°
APAP	2.45%	20.20 ms	5.92°
本文方法	1.02%	8.78 ms	1.42°

新窗口打开| 下载CSV

图6展示多组拼接测试结果以说明本文算法的综合表现能力.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 拼接结果

Fig.6 Panoramic stitching

3 结论

全景拼接比较容易出现扭曲，这主要是旋转角度和不同的景深带来的尺度不统一导致的，从二维图像组的角度去拼接得到全景图本是一个病态问题（三维投影尺度缺失、遮挡），正如无法从二维图直接恢复三维结构一样，但是仅对于拼接而言，其效果就是为了满足人的直观感受，做到尽可能地接近自然拍摄效果.本文通过对齐后的网格顶点优化生成了精度较高且分布均匀的匹配点，用于引导图像分块拼接，同时去除了动态目标的干扰因素造成的扭曲现象，拼接结果取得了自然平滑的表现，这得益于一个合适的缩放因子和旋转估计.人们视觉倾向于通过齐场景中的直线边缘来评估拼接的对齐效果，从这一关键点出发衍生了本文的直线对齐的优化项，每对直线的对齐可以估计一个相对的旋转角度，这为我们估计图像之间的旋转奠定了良好的基础，自然性的体现便是图像的旋转使得画布整体接近同一个拍摄角度.本文着重研究了匹配图自动生成、拼接自然性和动态目标去除，最后的目的就是能够满足更多的适应场景.在很多领域图像拼接依然面临着通用性和普适性问题，一个没有时序和空间序的拼接方案对于提高拼接应用的灵活性有很大的帮助，提升使用体验，这对相关产品的更新具有较大的意义，尤其是在三维重建和无人机航拍快速拼接中，具有重大意义.但是由于景深的问题，我们无法对尺度变换大的物体做出良好的适应性，这可能导致海拔高的物体在拼接后很难对齐，出现重影，投影的尺度无法恢复.而对于动态目标的检测和分割也需要更进一步的收集数据以增强学习，提高检测的精度.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Lee

K Y

， Sim

J Y

Warping residual based image stitching for large parallax

∥Proceedings of the 2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Seattle，WA，USA：IEEE，2020：8195-8203.