Deep neural networks for acoustic modeling in speech recognition:The shared views of four research groups
1
2012
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
Reservoir computing approaches to recurrent neural network training
1
2009
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
Spintronics for energy?efficient computing:An overview and outlook
2
2021
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 至此,我们的模拟结果和分析证明了高强度非线性“子弹”局域模是由局域在点电极边界A处的自旋流直接激发的,而在外围B区域的次强度准线性自旋波模是主模通过非线性倍频能量传输间接激发的,这些结果与之前的平面点接触自旋霍尔振荡器的微磁模拟和相关实验结果相类似[38-39].然而,不同于平面点接触自旋霍尔振荡器,我们的垂直点接触自旋霍尔振荡器中的自旋流具有手性对称性,自旋波只能在点接触一侧被激发,且其传播方向与外加磁场的面内方向垂直.因此,可以通过改变外加磁场的面内方向来调控自旋波空间分布及传播的方向,这非常有利于后期自旋波非线性耦合效应发展低功耗自旋波器件,如自旋波类脑计算硬件[4-11,19-20]. ...
Spintronic neuromorphic devices
0
2022
Recurrent neural networks made of magnetic tunnel junctions
0
2020
Spintronic devices for neuromorphic computing
1
2020
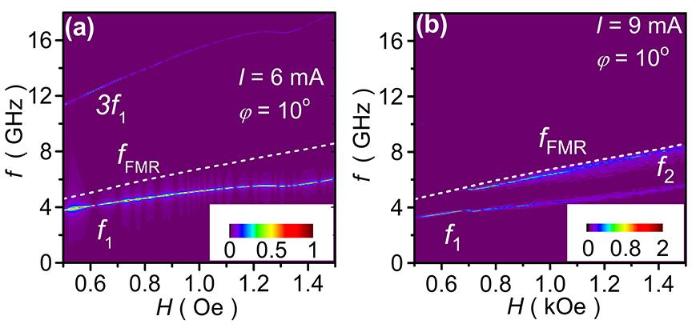
... 为了进一步研究其他实验参数对这类垂直点接触自旋霍尔振荡器的自旋波模式影响及依赖关系,对外加磁场大小和面外角度情况下的频谱特性进行了系列模拟计算和分析.图5为自旋霍尔振荡器在激发电流和下的频谱特性随外加磁场H变化的依赖关系.在低激发电流下,自旋霍尔振荡器在所有研究的磁场下()只能激发低频的局域“子弹”型孤波模[7]以及它的三次谐波模;而当增大电流到时,自旋霍尔振荡器在外加磁场强度大于的范围内,除了能激发局域“子弹”型孤波模,还能激发高频的准线性自旋波模.在所有研究磁场大小范围内,所激发的准线性自旋波模的频率与铁磁共振频率非常接近,与上述图3结果一致. ...
Neuro?morphic spintronics
0
2020
Voltage?controlled spintronic stochastic neuron based on a magnetic tunnel junction
0
2019
Physical reservoir computing using magnetic skyrmion memristor and spin torque Nano?oscillator
0
2019
基于磁性隧道结的群体编码实现无监督聚类
2
2022
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 至此,我们的模拟结果和分析证明了高强度非线性“子弹”局域模是由局域在点电极边界A处的自旋流直接激发的,而在外围B区域的次强度准线性自旋波模是主模通过非线性倍频能量传输间接激发的,这些结果与之前的平面点接触自旋霍尔振荡器的微磁模拟和相关实验结果相类似[38-39].然而,不同于平面点接触自旋霍尔振荡器,我们的垂直点接触自旋霍尔振荡器中的自旋流具有手性对称性,自旋波只能在点接触一侧被激发,且其传播方向与外加磁场的面内方向垂直.因此,可以通过改变外加磁场的面内方向来调控自旋波空间分布及传播的方向,这非常有利于后期自旋波非线性耦合效应发展低功耗自旋波器件,如自旋波类脑计算硬件[4-11,19-20]. ...
Implementation of unsupervised clustering based on population coding of magnetic tunnel junctions
2
2022
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 至此,我们的模拟结果和分析证明了高强度非线性“子弹”局域模是由局域在点电极边界A处的自旋流直接激发的,而在外围B区域的次强度准线性自旋波模是主模通过非线性倍频能量传输间接激发的,这些结果与之前的平面点接触自旋霍尔振荡器的微磁模拟和相关实验结果相类似[38-39].然而,不同于平面点接触自旋霍尔振荡器,我们的垂直点接触自旋霍尔振荡器中的自旋流具有手性对称性,自旋波只能在点接触一侧被激发,且其传播方向与外加磁场的面内方向垂直.因此,可以通过改变外加磁场的面内方向来调控自旋波空间分布及传播的方向,这非常有利于后期自旋波非线性耦合效应发展低功耗自旋波器件,如自旋波类脑计算硬件[4-11,19-20]. ...
Spin transfer torques
3
2008
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
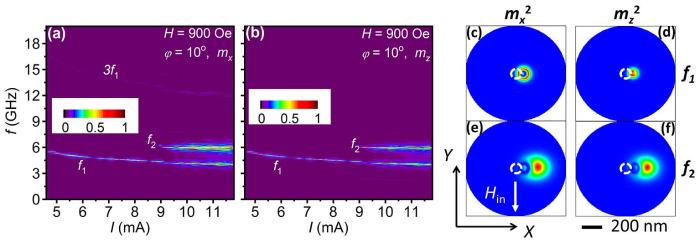
... 基于微磁模拟,能获得垂直点接触自旋霍尔纳米振荡器的频谱特性随激发电流大小变化的依赖关系.每个电流下的频谱曲线是通过对器件的平均磁化强度在x轴或y轴方向的分量随时间变化的振荡数据和进行快速傅里叶变换(FFT)得到的.如图3a和图3b所示,在外加磁场下,当激发电流达到临界值时,器件的频谱曲线在5.8 GHz处会突然出现一个振荡峰,被标注为低频自旋波模.该振荡模的频率低于其铁磁共振频率fFMR,且随激发电流的增加呈现明显的频率红移现象.当激发电流继续增加,达到时,除了低频自旋波模之外,在接近其铁磁共振频率处还会出现另外一个高频振荡峰,被标注为高频自旋波模,该自旋波模的频率随激发电流的增加基本保持不变.另外,高频自旋波模的出现也会导致低频自旋波模的线宽展宽,表明两种振荡模式间存在一定的相互作用.根据之前关于自旋力矩纳米振荡器的非线性理论和相关实验结果[26-28,38],能初步判断低频自旋波模是一类非线性局域的自旋孤波,也称为局域“子弹”型孤波[12],而高频自旋波模是一类准线性传播型自旋波[37,39,46].另外,从图3a中,还可以发现该振荡器还能激发出自旋波模的三次谐波,其频率远高于.为了进一步分析低频振荡模和高频振荡模的属性,对微磁模拟中的每个格点的磁矩随时间变化曲线和进行快速傅里叶变换,提取每个格点的和的频谱功率强度PFFT之后,再按照其原来的空间顺序进行排布,最后能得到振荡器在和模式下的功率密度空间分布.如图3c和图3d所示,低频振荡模局域在点电极边缘的右侧直径的圆形区域A内,这里的自旋流强度最大,且其自旋极化方向与外磁场方向(或平衡态磁矩矢量)相反.图3e和图3f显示,高频振荡模的强度分布在低频振荡模的右侧200 nm纵深的区域B内,其振荡区域大约是的2倍.这些特性与上面分析的局域“子弹”型孤波和准线性传播型自旋波相符. ...
Spin wave mode excited by spin?polarized current in a magnetic nanocontact is a standing self?localized wave bullet
0
2005
The dynamics of vertically coupled vortices excited by current with tilted spin polarization
0
2021
Spin transfer nano?oscillators
0
2014
自旋转矩纳米振荡器的研究进展
2
2013
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Recent research of spin torque nano?oscillator
2
2013
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Excitation of coherent propagating spin waves by pure spin currents
1
2016
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
1
2022
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
1
2022
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
Recent progress on excitation and manipulation of spin?waves in spin Hall Nano?oscillators
3
2020
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
... 至此,我们的模拟结果和分析证明了高强度非线性“子弹”局域模是由局域在点电极边界A处的自旋流直接激发的,而在外围B区域的次强度准线性自旋波模是主模通过非线性倍频能量传输间接激发的,这些结果与之前的平面点接触自旋霍尔振荡器的微磁模拟和相关实验结果相类似[38-39].然而,不同于平面点接触自旋霍尔振荡器,我们的垂直点接触自旋霍尔振荡器中的自旋流具有手性对称性,自旋波只能在点接触一侧被激发,且其传播方向与外加磁场的面内方向垂直.因此,可以通过改变外加磁场的面内方向来调控自旋波空间分布及传播的方向,这非常有利于后期自旋波非线性耦合效应发展低功耗自旋波器件,如自旋波类脑计算硬件[4-11,19-20]. ...
Opportunities and challenges for spintronics in the microelectronics industry
2
2020
... 神经网络算法对生物神经元的模拟需要计算和存储大量非线性信息,而随着所处理的问题复杂度和数据量的增加,基于冯诺依曼架构的传统半导体微电子技术难以提供满足各类复杂算法要求的高计算量、高并行度、低功耗的计算硬件[1-3].自旋电子学是研究电子内禀自旋及其应用的学科.目前大量研究表明,基于电子自旋特性设计的纳米自旋器件有望实现高集成度、高速、低功耗的新型非冯诺依曼架构用于模拟神经元和突触行为,进行高效的神经形态类脑计算,应用于当前如火如荼的人工智能领域[4-11].在多层磁性异质结(自旋阀和磁隧道结)体系中,利用自旋转移力矩(Spin⁃Transfer Torque,STT)效应在纳米磁性薄膜中能实现电流驱动其磁矩进行微波频段的高频振荡,激发相干自旋波,具有丰富的高频非线性效应[12-16],能作为微纳尺度的微波信号源或自旋波源[17-18],有望推进片上集成的无线通信技术和模拟神经形态计算的发展[19-20]. ...
... 至此,我们的模拟结果和分析证明了高强度非线性“子弹”局域模是由局域在点电极边界A处的自旋流直接激发的,而在外围B区域的次强度准线性自旋波模是主模通过非线性倍频能量传输间接激发的,这些结果与之前的平面点接触自旋霍尔振荡器的微磁模拟和相关实验结果相类似[38-39].然而,不同于平面点接触自旋霍尔振荡器,我们的垂直点接触自旋霍尔振荡器中的自旋流具有手性对称性,自旋波只能在点接触一侧被激发,且其传播方向与外加磁场的面内方向垂直.因此,可以通过改变外加磁场的面内方向来调控自旋波空间分布及传播的方向,这非常有利于后期自旋波非线性耦合效应发展低功耗自旋波器件,如自旋波类脑计算硬件[4-11,19-20]. ...
Spin?transfer torque generated by a topological insulator
1
2014
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Maximizing spin–orbit torque efficiency of Ta(O)/Py via modu?lating oxygen?induced interface orbital hybridization
1
2021
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Quantum materials for spin and charge conversion
1
2018
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Spin?torque switching with the giant spin hall effect of Tantalum
1
2012
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Magnetic nano?oscillator driven by pure spin current
1
2012
... 基于微磁模拟,能获得垂直点接触自旋霍尔纳米振荡器的频谱特性随激发电流大小变化的依赖关系.每个电流下的频谱曲线是通过对器件的平均磁化强度在x轴或y轴方向的分量随时间变化的振荡数据和进行快速傅里叶变换(FFT)得到的.如图3a和图3b所示,在外加磁场下,当激发电流达到临界值时,器件的频谱曲线在5.8 GHz处会突然出现一个振荡峰,被标注为低频自旋波模.该振荡模的频率低于其铁磁共振频率fFMR,且随激发电流的增加呈现明显的频率红移现象.当激发电流继续增加,达到时,除了低频自旋波模之外,在接近其铁磁共振频率处还会出现另外一个高频振荡峰,被标注为高频自旋波模,该自旋波模的频率随激发电流的增加基本保持不变.另外,高频自旋波模的出现也会导致低频自旋波模的线宽展宽,表明两种振荡模式间存在一定的相互作用.根据之前关于自旋力矩纳米振荡器的非线性理论和相关实验结果[26-28,38],能初步判断低频自旋波模是一类非线性局域的自旋孤波,也称为局域“子弹”型孤波[12],而高频自旋波模是一类准线性传播型自旋波[37,39,46].另外,从图3a中,还可以发现该振荡器还能激发出自旋波模的三次谐波,其频率远高于.为了进一步分析低频振荡模和高频振荡模的属性,对微磁模拟中的每个格点的磁矩随时间变化曲线和进行快速傅里叶变换,提取每个格点的和的频谱功率强度PFFT之后,再按照其原来的空间顺序进行排布,最后能得到振荡器在和模式下的功率密度空间分布.如图3c和图3d所示,低频振荡模局域在点电极边缘的右侧直径的圆形区域A内,这里的自旋流强度最大,且其自旋极化方向与外磁场方向(或平衡态磁矩矢量)相反.图3e和图3f显示,高频振荡模的强度分布在低频振荡模的右侧200 nm纵深的区域B内,其振荡区域大约是的2倍.这些特性与上面分析的局域“子弹”型孤波和准线性传播型自旋波相符. ...
Spectral charac?teristics of the microwave emission by the spin hall nano?oscillator
0
2013
Spin?orbit?torque efficiency and current?driven coherent magnetic dynamics in a Pt/Ni/Py trilayer?based spin hall Nano?oscillator
2
2022
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
... 基于微磁模拟,能获得垂直点接触自旋霍尔纳米振荡器的频谱特性随激发电流大小变化的依赖关系.每个电流下的频谱曲线是通过对器件的平均磁化强度在x轴或y轴方向的分量随时间变化的振荡数据和进行快速傅里叶变换(FFT)得到的.如图3a和图3b所示,在外加磁场下,当激发电流达到临界值时,器件的频谱曲线在5.8 GHz处会突然出现一个振荡峰,被标注为低频自旋波模.该振荡模的频率低于其铁磁共振频率fFMR,且随激发电流的增加呈现明显的频率红移现象.当激发电流继续增加,达到时,除了低频自旋波模之外,在接近其铁磁共振频率处还会出现另外一个高频振荡峰,被标注为高频自旋波模,该自旋波模的频率随激发电流的增加基本保持不变.另外,高频自旋波模的出现也会导致低频自旋波模的线宽展宽,表明两种振荡模式间存在一定的相互作用.根据之前关于自旋力矩纳米振荡器的非线性理论和相关实验结果[26-28,38],能初步判断低频自旋波模是一类非线性局域的自旋孤波,也称为局域“子弹”型孤波[12],而高频自旋波模是一类准线性传播型自旋波[37,39,46].另外,从图3a中,还可以发现该振荡器还能激发出自旋波模的三次谐波,其频率远高于.为了进一步分析低频振荡模和高频振荡模的属性,对微磁模拟中的每个格点的磁矩随时间变化曲线和进行快速傅里叶变换,提取每个格点的和的频谱功率强度PFFT之后,再按照其原来的空间顺序进行排布,最后能得到振荡器在和模式下的功率密度空间分布.如图3c和图3d所示,低频振荡模局域在点电极边缘的右侧直径的圆形区域A内,这里的自旋流强度最大,且其自旋极化方向与外磁场方向(或平衡态磁矩矢量)相反.图3e和图3f显示,高频振荡模的强度分布在低频振荡模的右侧200 nm纵深的区域B内,其振荡区域大约是的2倍.这些特性与上面分析的局域“子弹”型孤波和准线性传播型自旋波相符. ...
Effect of Oersted field on the localized droplet mode and propagating spin waves mode excited in spin?torque nano?oscillator
1
2021
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Opportunities at the frontiers of spintronics
1
2015
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Prospect of spin?orbitronic devices and their applications
0
2020
自旋霍尔纳米振荡器的非线性动力学及其应用
2
2020
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
... ,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Nonlinear dynamics and applications of spin hall nano?oscillators
2
2020
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
... ,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Collimated bidirectional propagating spin wave generated by a nonlocal spin?current nano?oscillator
1
2021
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Experiments and SPICE simulations of double MgO?based perpen?dicular magnetic tunnel junction
1
2021
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Field? and current?driven magnetization reversal and dynamic properties of CoFeB?MgO?based perpendicular magnetic tunnel junctions
0
2020
Highly efficient spin?orbit torque in a perpendicular synthetic ferrimagnet
1
2022
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Emission of coherent propagating magnons by insulator?based spin?orbit?torque oscillators
2
2018
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
... 基于微磁模拟,能获得垂直点接触自旋霍尔纳米振荡器的频谱特性随激发电流大小变化的依赖关系.每个电流下的频谱曲线是通过对器件的平均磁化强度在x轴或y轴方向的分量随时间变化的振荡数据和进行快速傅里叶变换(FFT)得到的.如图3a和图3b所示,在外加磁场下,当激发电流达到临界值时,器件的频谱曲线在5.8 GHz处会突然出现一个振荡峰,被标注为低频自旋波模.该振荡模的频率低于其铁磁共振频率fFMR,且随激发电流的增加呈现明显的频率红移现象.当激发电流继续增加,达到时,除了低频自旋波模之外,在接近其铁磁共振频率处还会出现另外一个高频振荡峰,被标注为高频自旋波模,该自旋波模的频率随激发电流的增加基本保持不变.另外,高频自旋波模的出现也会导致低频自旋波模的线宽展宽,表明两种振荡模式间存在一定的相互作用.根据之前关于自旋力矩纳米振荡器的非线性理论和相关实验结果[26-28,38],能初步判断低频自旋波模是一类非线性局域的自旋孤波,也称为局域“子弹”型孤波[12],而高频自旋波模是一类准线性传播型自旋波[37,39,46].另外,从图3a中,还可以发现该振荡器还能激发出自旋波模的三次谐波,其频率远高于.为了进一步分析低频振荡模和高频振荡模的属性,对微磁模拟中的每个格点的磁矩随时间变化曲线和进行快速傅里叶变换,提取每个格点的和的频谱功率强度PFFT之后,再按照其原来的空间顺序进行排布,最后能得到振荡器在和模式下的功率密度空间分布.如图3c和图3d所示,低频振荡模局域在点电极边缘的右侧直径的圆形区域A内,这里的自旋流强度最大,且其自旋极化方向与外磁场方向(或平衡态磁矩矢量)相反.图3e和图3f显示,高频振荡模的强度分布在低频振荡模的右侧200 nm纵深的区域B内,其振荡区域大约是的2倍.这些特性与上面分析的局域“子弹”型孤波和准线性传播型自旋波相符. ...
Dynamical mode coexistence and chaos in a nanogap Spin Hall nano?oscillator
3
2019
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
... 基于微磁模拟,能获得垂直点接触自旋霍尔纳米振荡器的频谱特性随激发电流大小变化的依赖关系.每个电流下的频谱曲线是通过对器件的平均磁化强度在x轴或y轴方向的分量随时间变化的振荡数据和进行快速傅里叶变换(FFT)得到的.如图3a和图3b所示,在外加磁场下,当激发电流达到临界值时,器件的频谱曲线在5.8 GHz处会突然出现一个振荡峰,被标注为低频自旋波模.该振荡模的频率低于其铁磁共振频率fFMR,且随激发电流的增加呈现明显的频率红移现象.当激发电流继续增加,达到时,除了低频自旋波模之外,在接近其铁磁共振频率处还会出现另外一个高频振荡峰,被标注为高频自旋波模,该自旋波模的频率随激发电流的增加基本保持不变.另外,高频自旋波模的出现也会导致低频自旋波模的线宽展宽,表明两种振荡模式间存在一定的相互作用.根据之前关于自旋力矩纳米振荡器的非线性理论和相关实验结果[26-28,38],能初步判断低频自旋波模是一类非线性局域的自旋孤波,也称为局域“子弹”型孤波[12],而高频自旋波模是一类准线性传播型自旋波[37,39,46].另外,从图3a中,还可以发现该振荡器还能激发出自旋波模的三次谐波,其频率远高于.为了进一步分析低频振荡模和高频振荡模的属性,对微磁模拟中的每个格点的磁矩随时间变化曲线和进行快速傅里叶变换,提取每个格点的和的频谱功率强度PFFT之后,再按照其原来的空间顺序进行排布,最后能得到振荡器在和模式下的功率密度空间分布.如图3c和图3d所示,低频振荡模局域在点电极边缘的右侧直径的圆形区域A内,这里的自旋流强度最大,且其自旋极化方向与外磁场方向(或平衡态磁矩矢量)相反.图3e和图3f显示,高频振荡模的强度分布在低频振荡模的右侧200 nm纵深的区域B内,其振荡区域大约是的2倍.这些特性与上面分析的局域“子弹”型孤波和准线性传播型自旋波相符. ...
... 至此,我们的模拟结果和分析证明了高强度非线性“子弹”局域模是由局域在点电极边界A处的自旋流直接激发的,而在外围B区域的次强度准线性自旋波模是主模通过非线性倍频能量传输间接激发的,这些结果与之前的平面点接触自旋霍尔振荡器的微磁模拟和相关实验结果相类似[38-39].然而,不同于平面点接触自旋霍尔振荡器,我们的垂直点接触自旋霍尔振荡器中的自旋流具有手性对称性,自旋波只能在点接触一侧被激发,且其传播方向与外加磁场的面内方向垂直.因此,可以通过改变外加磁场的面内方向来调控自旋波空间分布及传播的方向,这非常有利于后期自旋波非线性耦合效应发展低功耗自旋波器件,如自旋波类脑计算硬件[4-11,19-20]. ...
Dynamical mode coupling and coherence in a spin hall nano?oscillator with perpendicular magnetic anisotropy
2
2019
... 基于微磁模拟,能获得垂直点接触自旋霍尔纳米振荡器的频谱特性随激发电流大小变化的依赖关系.每个电流下的频谱曲线是通过对器件的平均磁化强度在x轴或y轴方向的分量随时间变化的振荡数据和进行快速傅里叶变换(FFT)得到的.如图3a和图3b所示,在外加磁场下,当激发电流达到临界值时,器件的频谱曲线在5.8 GHz处会突然出现一个振荡峰,被标注为低频自旋波模.该振荡模的频率低于其铁磁共振频率fFMR,且随激发电流的增加呈现明显的频率红移现象.当激发电流继续增加,达到时,除了低频自旋波模之外,在接近其铁磁共振频率处还会出现另外一个高频振荡峰,被标注为高频自旋波模,该自旋波模的频率随激发电流的增加基本保持不变.另外,高频自旋波模的出现也会导致低频自旋波模的线宽展宽,表明两种振荡模式间存在一定的相互作用.根据之前关于自旋力矩纳米振荡器的非线性理论和相关实验结果[26-28,38],能初步判断低频自旋波模是一类非线性局域的自旋孤波,也称为局域“子弹”型孤波[12],而高频自旋波模是一类准线性传播型自旋波[37,39,46].另外,从图3a中,还可以发现该振荡器还能激发出自旋波模的三次谐波,其频率远高于.为了进一步分析低频振荡模和高频振荡模的属性,对微磁模拟中的每个格点的磁矩随时间变化曲线和进行快速傅里叶变换,提取每个格点的和的频谱功率强度PFFT之后,再按照其原来的空间顺序进行排布,最后能得到振荡器在和模式下的功率密度空间分布.如图3c和图3d所示,低频振荡模局域在点电极边缘的右侧直径的圆形区域A内,这里的自旋流强度最大,且其自旋极化方向与外磁场方向(或平衡态磁矩矢量)相反.图3e和图3f显示,高频振荡模的强度分布在低频振荡模的右侧200 nm纵深的区域B内,其振荡区域大约是的2倍.这些特性与上面分析的局域“子弹”型孤波和准线性传播型自旋波相符. ...
... 至此,我们的模拟结果和分析证明了高强度非线性“子弹”局域模是由局域在点电极边界A处的自旋流直接激发的,而在外围B区域的次强度准线性自旋波模是主模通过非线性倍频能量传输间接激发的,这些结果与之前的平面点接触自旋霍尔振荡器的微磁模拟和相关实验结果相类似[38-39].然而,不同于平面点接触自旋霍尔振荡器,我们的垂直点接触自旋霍尔振荡器中的自旋流具有手性对称性,自旋波只能在点接触一侧被激发,且其传播方向与外加磁场的面内方向垂直.因此,可以通过改变外加磁场的面内方向来调控自旋波空间分布及传播的方向,这非常有利于后期自旋波非线性耦合效应发展低功耗自旋波器件,如自旋波类脑计算硬件[4-11,19-20]. ...
Magnetic droplet mode in a vertical nanocontact?based Spin Hall nano?oscillator at oblique fields
0
2020
Controllable excitation of multiple spin wave bullet modes in a Spin Hall nano?oscillator based on multilayers
0
2021
Spatial coexistence of multiple modes in a nanogap spin Hall nano?oscillator with extended Pt/Ni/Fe trilayers
0
2022
Long?range mutual synchronization of spin Hall nano?oscillators
0
2017
Two?dimensional mutually synchronized Spin Hall nano?oscillator arrays for neuromorphic computing
1
2020
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Spin?wave?mode coexistence on the nanoscale:a consequence of the oersted?field?induced asymmetric energy landscape
1
2013
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
Controlled nonlinear magnetic damping in Spin?Hall nano?devices
2
2019
... 除了多层磁性异质结中的自旋转移力矩效应,最近,在铁磁/重金属或拓扑材料双层结构中发现强自旋霍尔和界面Rashba效应[21-23],利用其产生的纯自旋流实现高效的电流调控邻近磁性层的磁矩翻转或激发相干自旋波[24-29],从而有望革新当前自旋电子学技术[30-32].另外,这种自旋轨道效应产生的纯自旋流与电荷电流方向是相互垂直的,能实现空间上相互分离,因此,纯自旋流操控自旋的方式能最大限度地减少电荷电流引起的焦耳热和奥斯特场对器件核心区域产生的副效应[33],实现高速磁随机存储器(MRAM)[34-36]和自旋纳米振荡器(Spin⁃Transfer Torque Nano⁃Oscillator,STNO).因此,近年来,在这类纯自旋流器件中,利用电流产生的自旋轨道力矩(Spin⁃Orbit Torque,SOT)[12-16]驱动可控磁翻转和激发相干自旋波进行了深入研究[25-28],其中,结构简单和重复性高的自旋霍尔纳米振荡器(Spin⁃Hall Nano Oscillator,SHNO)能应用于各类自旋极化材料(如重金属及氧化物,拓扑绝缘体,外尔半金属等)和磁性材料(如低阻尼金属和绝缘体)体系[19,32,37],因此,近年来受到越来越多研究者的关注和深入研究[38-44].例如前期微波谱实验发现自旋霍尔纳米振荡器中纯自旋流激发的自旋波非线性动力学现象(如:自旋波模式的退相干、共存、跳变和同步、非线性耦合导致磁阻尼等)与电流产生的奥斯特磁场和自旋流的自旋极化方向及密度分布、磁各向异性以及外加磁场角度等参数密切相关[45-46],其具体依赖关系和背后物理机制还有待进一步深入研究. ...
... 基于微磁模拟,能获得垂直点接触自旋霍尔纳米振荡器的频谱特性随激发电流大小变化的依赖关系.每个电流下的频谱曲线是通过对器件的平均磁化强度在x轴或y轴方向的分量随时间变化的振荡数据和进行快速傅里叶变换(FFT)得到的.如图3a和图3b所示,在外加磁场下,当激发电流达到临界值时,器件的频谱曲线在5.8 GHz处会突然出现一个振荡峰,被标注为低频自旋波模.该振荡模的频率低于其铁磁共振频率fFMR,且随激发电流的增加呈现明显的频率红移现象.当激发电流继续增加,达到时,除了低频自旋波模之外,在接近其铁磁共振频率处还会出现另外一个高频振荡峰,被标注为高频自旋波模,该自旋波模的频率随激发电流的增加基本保持不变.另外,高频自旋波模的出现也会导致低频自旋波模的线宽展宽,表明两种振荡模式间存在一定的相互作用.根据之前关于自旋力矩纳米振荡器的非线性理论和相关实验结果[26-28,38],能初步判断低频自旋波模是一类非线性局域的自旋孤波,也称为局域“子弹”型孤波[12],而高频自旋波模是一类准线性传播型自旋波[37,39,46].另外,从图3a中,还可以发现该振荡器还能激发出自旋波模的三次谐波,其频率远高于.为了进一步分析低频振荡模和高频振荡模的属性,对微磁模拟中的每个格点的磁矩随时间变化曲线和进行快速傅里叶变换,提取每个格点的和的频谱功率强度PFFT之后,再按照其原来的空间顺序进行排布,最后能得到振荡器在和模式下的功率密度空间分布.如图3c和图3d所示,低频振荡模局域在点电极边缘的右侧直径的圆形区域A内,这里的自旋流强度最大,且其自旋极化方向与外磁场方向(或平衡态磁矩矢量)相反.图3e和图3f显示,高频振荡模的强度分布在低频振荡模的右侧200 nm纵深的区域B内,其振荡区域大约是的2倍.这些特性与上面分析的局域“子弹”型孤波和准线性传播型自旋波相符. ...
Stockholm,Sweden:COMSOL AB
1
... 为了量化器件的电流和奥斯特磁场的空间分布作为下面微磁模拟的参数,利用多物理场有限元模拟软件COMSOL MULTIPHYSICS对上述器件结构进行准平衡静态电和磁相关仿真计算[47].图2a是重金属层中电流密度的二维平面矢量及强度分布图.电流从环形金电极通过铁磁/重金属双层均匀地聚集到薄膜中心,再经过直径的点电极流出器件薄膜.电流的这种径向流动,使得铁磁/重金属双层中的电流密度在点电极边缘到达最大(红色环形区域).图2b展示了由电流产生的面内奥斯特场在铁磁层中的方向及强度分布图,其最大值也局域在点电极边缘区域.由于重金属层的自旋霍尔效应,重金属层中的电流也将产生垂直于器件平面流向的自旋流,注入上层铁磁多层.如图2c所示,自旋流的极化方向与圆盘径向方向垂直,与面内奥斯特场相类似,其强度也局域在点电极边缘.需要强调的是,在这类强自旋霍尔体系中,下面的微磁学模拟我们仅考虑了面内自旋极化的自旋流,而最近研究发现,在一些具有自旋轨道耦合的铁磁体中,由于自旋交换效应(Spin Swapping Effect),会导致部分面外自旋极化的自旋流[48]. ...
Observation of nontrivial spin?orbit torque in single?layer ferromagnetic metals
1
2022
... 为了量化器件的电流和奥斯特磁场的空间分布作为下面微磁模拟的参数,利用多物理场有限元模拟软件COMSOL MULTIPHYSICS对上述器件结构进行准平衡静态电和磁相关仿真计算[47].图2a是重金属层中电流密度的二维平面矢量及强度分布图.电流从环形金电极通过铁磁/重金属双层均匀地聚集到薄膜中心,再经过直径的点电极流出器件薄膜.电流的这种径向流动,使得铁磁/重金属双层中的电流密度在点电极边缘到达最大(红色环形区域).图2b展示了由电流产生的面内奥斯特场在铁磁层中的方向及强度分布图,其最大值也局域在点电极边缘区域.由于重金属层的自旋霍尔效应,重金属层中的电流也将产生垂直于器件平面流向的自旋流,注入上层铁磁多层.如图2c所示,自旋流的极化方向与圆盘径向方向垂直,与面内奥斯特场相类似,其强度也局域在点电极边缘.需要强调的是,在这类强自旋霍尔体系中,下面的微磁学模拟我们仅考虑了面内自旋极化的自旋流,而最近研究发现,在一些具有自旋轨道耦合的铁磁体中,由于自旋交换效应(Spin Swapping Effect),会导致部分面外自旋极化的自旋流[48]. ...
OOMMF(NIST)
1
... 使用开源软件OOMMF对上述器件结构进行微磁学模拟[49],其材料参数如下:铁磁层的饱和磁化强度;磁交换常数;界面垂直各向异性系数;自旋霍尔角为0.05,磁性阻尼因子为0.03.为了避免圆盘边界对自旋波的反射,把边界区域的阻尼因子设为1,用于吸收中心区域发射的自旋波.最小微磁模拟单元尺寸为,整个微磁模拟尺寸为直径的圆盘,厚度为;外加磁场方向固定在轴的负方向,且与器件平面成的面外角().电流从环形电极流向点电极的方向定义为正电流方向. ...
1
2020
... 然而,从图2c所显示的自旋流强度分布图可以看出,高频准线性传播型自旋波模的空间分布区域处的自旋流密度相对比较低,为何会在此处激发高频的自旋波呢?为了探讨其中的原因,对A和B两个区域的平均磁矩矢量 M 随时间变化的进动三维轨迹图进行分析.图4a显示主导型“子弹”局域模在A区域的磁矩振荡是绕y轴方向的椭圆形进动,磁矩矢量 Mx 在x轴和z轴方向振幅到达90%以上,在y轴(其绕轴方向)方向振幅也到达60%以上,且其y轴方向的振荡频率是x轴和z轴方向振荡频率的2倍.因此,这类高振荡幅值椭圆型进动在分量上会产生很强的二次谐波.基于自旋波模之间的非线性耦合,该二次谐波通过参数泵浦(Parameter Pump)方式把系统能量从主导型“子弹”局域模传输给其他自旋波模[50-51],从而在大电流下通过这种能量传递过程在外围区域B处实现高频的准线性传播型自旋波模的激发.这个过程也解释了图3a中模为何在出现之后表现出明显的线宽展宽行为.图4(b)显示次强度振荡模在B区域的磁矩进动轨迹,磁矩矢量也是绕y轴方向进行椭圆形进动,主要沿轴振荡(振幅达),在轴方向振幅最高只有,在y轴(其绕轴方向)方向振幅为,所以分量依然会产生较强的二次谐波振荡信号. ...
The theory of ferromagnetic resonance at high signal powers
1
1957
... 然而,从图2c所显示的自旋流强度分布图可以看出,高频准线性传播型自旋波模的空间分布区域处的自旋流密度相对比较低,为何会在此处激发高频的自旋波呢?为了探讨其中的原因,对A和B两个区域的平均磁矩矢量 M 随时间变化的进动三维轨迹图进行分析.图4a显示主导型“子弹”局域模在A区域的磁矩振荡是绕y轴方向的椭圆形进动,磁矩矢量 Mx 在x轴和z轴方向振幅到达90%以上,在y轴(其绕轴方向)方向振幅也到达60%以上,且其y轴方向的振荡频率是x轴和z轴方向振荡频率的2倍.因此,这类高振荡幅值椭圆型进动在分量上会产生很强的二次谐波.基于自旋波模之间的非线性耦合,该二次谐波通过参数泵浦(Parameter Pump)方式把系统能量从主导型“子弹”局域模传输给其他自旋波模[50-51],从而在大电流下通过这种能量传递过程在外围区域B处实现高频的准线性传播型自旋波模的激发.这个过程也解释了图3a中模为何在出现之后表现出明显的线宽展宽行为.图4(b)显示次强度振荡模在B区域的磁矩进动轨迹,磁矩矢量也是绕y轴方向进行椭圆形进动,主要沿轴振荡(振幅达),在轴方向振幅最高只有,在y轴(其绕轴方向)方向振幅为,所以分量依然会产生较强的二次谐波振荡信号. ...