基于后向气团轨迹的大气污染特征时序混合模型研究

doi:10.13232/j.cnki.jnju.2022.06.012

基于后向气团轨迹的大气污染特征时序混合模型研究

许睿¹, 刘相阳¹, 文益民¹, 沈世铭², 李建^,¹

1.桂林电子科技大学计算机与信息安全学院, 桂林, 541004

2.卫星导航定位与位置服务国家地方联合工程研究中心, 桂林, 541004

Research on time series hybrid model of air pollution characteristics based on backward air mass trajectory

Xu Rui¹, Liu Xiangyang¹, Wen Yimin¹, Shen Shiming², Li Jian^,¹

1.School of Computer Science and Information Security，Guilin University of Electronic Technology，Guilin，541004，China

2.Satellite Navigation Positioning and Location Service National & Local Joint Engineering Research Center，Guilin，541004，China

通讯作者: E⁃mail：lijian@guet.edu.cn

收稿日期: 2022-07-04

基金资助:

广西自然科学基金.  2021GXNSFAA220056
广西重点研发计划.  AB21196063
国家自然科学基金.  62266014
桂林市重大成果转化基金.  20192013⁃1
桂林电子科技大学大学生创新创业训练计划.  202010595031

Received: 2022-07-04

摘要

由于大气污染监测数据量大且具备长时序特征，深度学习领域已将其作为一种标准数据集使用.针对现有大气污染预测方法未能结合大气传输的物理机理和有效考虑污染物传输的时空特征等问题，提出一种基于多模型混合的特征与时序污染物预测模型，利用HYSPLIT （Hybrid Single⁃Particle Lagrangian Integrated Trajectory）计算后向气团运动轨迹，引入VGG （Visual Geometry Group）模型提取气团轨迹线的变化特征；将其与污染物和气象时序数据结合，输入LSTM （Long Short⁃Term Memory）模型，预测研究区域内的目标污染物浓度，以评估研究区域的空气质量状况.以桂林市61个空气质量监测站点的污染物和相关气象在线监测数据为基础，对模型性能进行了评估，将实验结果与几种先进的方法进行了比较.结果表明，提出的H⁃VGG⁃LSTM （HYSPLIT⁃VGG⁃LSTM）模型有效提高了大气污染物的预测准确度，其预测结果的RMSE （Root Mean Squared Error），MAE （Mean Absolute Error）和SMAPE （Symmetric Mean Absolute Percentage Error）分别为0.202，1.198和1.97%，预测性能和其他先进模型相比有明显的提升.证明该模型对复杂气象条件下的污染物预测更准确，并具有较好的泛化性能.

关键词： 大气污染预测 ; PM_2.5 ; 后向轨迹模拟 ; 卷积神经网络 ; LSTM

Abstract

Deep learning uses air pollution monitoring data as a standard data set because of its huge number and characteristics of long time series. Aiming at the problems that the existing air pollution prediction methods fail to combine the physical mechanism of atmospheric transport and effectively consider the spatio⁃temporal characteristics of pollutant transport，in this paper，a feature and time series pollutant prediction model based on multi⁃model is proposed. Backward air mass trajectories are calculated using HYSPLIT (Hybrid Single⁃Particle Lagrangian Integrated Trajectory)，and the VGG (Convolutional Neural Networks) is introduced to extract the change characteristics of the air mass trajectory. The characteristics is combined with pollutant and meteorological time series data as the input of LSTM (Long Short⁃Term Memory)，then the predicted value of target pollutant concentration in the study area is obtained to evaluate the air quality of the study area. Based on the pollutants and related meteorological online monitoring data from 61 air quality monitoring stations in Guilin，the model performance is evaluated. Experimental results are compared with several state⁃of⁃the⁃art methods，which show that the proposed HYSPLIT⁃VGG⁃LSTM (H⁃VGG⁃LSTM) model effectively improves the prediction accuracy of atmospheric pollutants. RMSE(The Root Mean Square Error)，MAE(Mean Absolute Error)，and SMAPE (Symmetric Mean Absolute Percentage Error) of the prediction results are 0.202，1.198，and 1.97% respectively，and the prediction performance of the model is significantly improved compared with other advanced models. It is proved that the proposed model is more accurate in forecasting pollutants for complex meteorological conditions and has better generalization performance.

Keywords： air pollution prediction ; PM_2.5 ; backward trajectory simulation ; convolutional neural network ; LSTM

PDF (1360KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

许睿, 刘相阳, 文益民, 沈世铭, 李建. 基于后向气团轨迹的大气污染特征时序混合模型研究. 南京大学学报（自然科学）[J], 2022, 58(6): 1041-1049 doi:10.13232/j.cnki.jnju.2022.06.012

Xu Rui, Liu Xiangyang, Wen Yimin, Shen Shiming, Li Jian. Research on time series hybrid model of air pollution characteristics based on backward air mass trajectory. Journal of nanjing University[J], 2022, 58(6): 1041-1049 doi:10.13232/j.cnki.jnju.2022.06.012

随着社会经济的发展和科技的进步，城市化和工业化的扩张对桂林地区空气质量的威胁越来越严重.区域大气污染物的预测对空气质量状况的控制至关重要^［1］，但是传统预测方法对于地形和气象复杂地区的预测效果较差.因此，结合气候变量和排放源开展对当地区域大气污染物的准确预测，已经具备了实用和学术价值.

目前，大气污染物的预测方法主要有传统物理模型、机器学习模型和深度学习模型.物理模型主要通过模拟大气污染的扩散和传输机理来预测大气污染物^［2-3］.例如，Rangel et al^［4］利用AERMOD VIEW模拟软件估算巴西东北部农村排放的CO，PM_2.5和NO _x 的体积和在大气中的扩散情况.Zhang et al^［5］提出一种结合风向的插值算法Win⁃OK，利用新乡市的数据集进行验证.Chen et al^［6］将NO₂的插值结果作为LUR（Land Use Regression）建模的变量的预测模型，提高了台湾地区NO₂的预测精度.Wang et al^［7］使用嵌套空气质量预测建模系统（NAQPMS），校准了PM_2.5浓度值.由于大气中气溶胶化学和动力学机制存在不确定性，扩散和化学传输模型等基于物理的模型仍在开发中^［8-12］.此外，默认参数的使用和缺乏实际观察结果限制了其在非线性问题中的准确性.

为了克服物理模型的局限性，有学者尝试采用机器学习模型.赵文怡等^［13］通过加权KNN⁃BP神经网络模型，预测了北京市东城区PM_2.5浓度的动态变化.车磊等^［14］提出一种基于多尺度最小二乘支持向量机优化的克里金插值方法，估测了青岛市PM_2.5浓度的时空分布特征.Alimissis et al^［15］使用人工神经网络（Artificial Neural Network，ANN）和多元线性回归（Multiple Linear Regression，MLR），实现了对希腊主要污染物浓度的高精度预测.Ortiz⁃Garcia et al^［16］基于支持向量机（Support Vector Machine，SVM）、多层感知器（Multi⁃Layer Perceptron，MLP）和向量自回归移动平均（Vector Autoregressive Moving Average，VARMA）等开发的模型预测西班牙北部的PM₁₀浓度.尽管非线性机器学习模型在预测大气污染领域已经获得了良好的性能，但对于捕捉时序数据的长期依赖仍具有局限性.

为了从时序数据中获得更多信息，有学者开始使用深度学习模型^［17-20］.例如，Qin et al^［21］将卷积神经网络（Convolutional Neural Networks，CNN）与长短期记忆网络（Long Short⁃Term Memory，LSTM）结合，预测上海市的PM_2.5浓度.Ma et al^［22］开发了一种基于迁移学习的堆叠式双向长短时记忆网络（Transfer Learning⁃Based Stacked Bidirectional Long Short Term Memory，TLS⁃BLSTM），提高了安徽省PM_2.5，NO₂和O₃的预测精度.Ding et al^［23］利用加利福尼亚州PM_2.5数据，证明相关滤波时空长短期记忆（Correlation Filtered Spatial⁃Temporal Long Short⁃Term，CFST⁃LSTM）模型能有效提高预测精度.尽管深度学习模型可以从数据中更好地捕获时序信息^［24-25］，且已经在大气污染预测中获得良好的结果，但是其缺少对研究区域内空间特征的考虑^［26-28］，或考虑不够充分^［29-30］，无法有效解释大气污染传输机理.

针对上述问题，提出基于后向气团轨迹的大气污染特征时序混合模型.本研究的主要贡献：

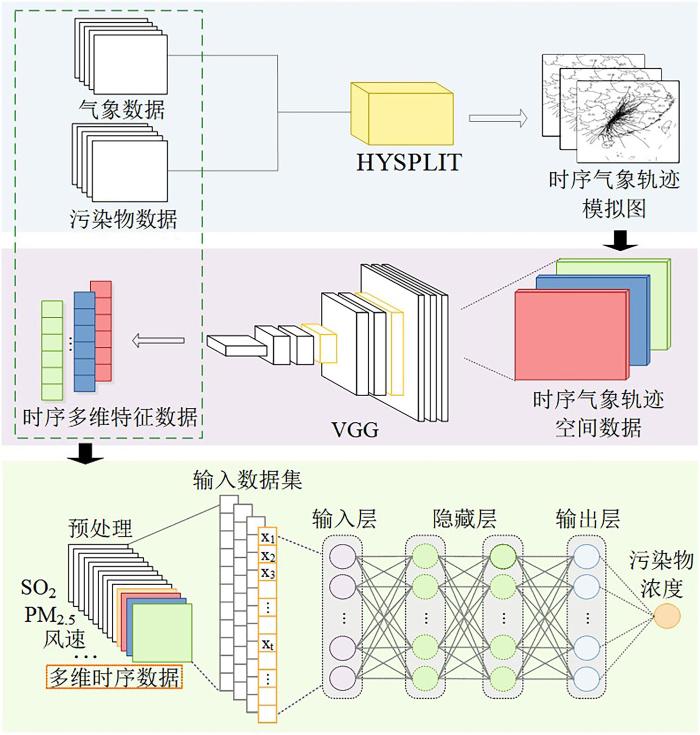
（1）将HYSPLIT （Hybrid Single⁃Particle Lagrangian Integrated Trajectory）与VGG （Visual Geometry Group）组合，提取气象传输特征并获得时序大气传输高维特征值，结合气象数据和其他污染物数据序列构成LSTM的输入数据集.

（2）利用LSTM分析污染物、气象和大气传输高维特征值，对研究区域内的目标污染物浓度进行预测.

（3）通过对比实验，证明提出的多模型混合预测方法可以有效提高气象复杂地区的目标污染物浓度预测精度.通过消融实验，验证了考虑污染物传输空间特征信息的必要性.

1 研究区概况及研究数据

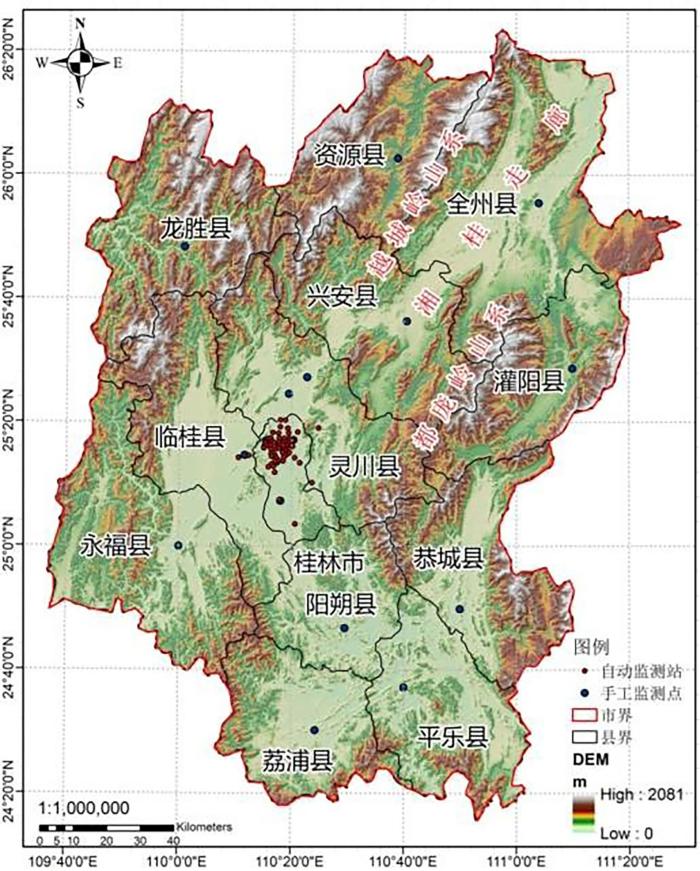
桂林市位于中国广西东北部，位于109°36′~111°29′ E，24°15′~26°23′ N，境内为典型的“喀斯特”岩溶地貌，支流河谷两侧多悬崖峭壁，有利于山谷环流的形成.桂林市东北方和南方皆毗邻重工业市，东北部为狭长的气团走向带“湘桂走廊”，利于外部气团的输入.因此，整体区域适用于大气污染物预测模型的研究.

桂林市有61处大气质量监测站，站点位置分布如图1所示.研究数据包括2017-2020年的污染物及气象的小时级监测数据，污染物数据包括PM_2.5，PM₁₀和NO₂等指标，气象数据包括大气温度、湿度和风向等指标.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 桂林市的地形和监测站分布

Fig.1 The topography and distribution of monitoring stations in Guilin

选择2016-2019年度数据作为基准数据集，具体如表1所示.PM_2.5和PM₁₀作为评价空气质量状况的核心指标，能够客观反映大气污染变化情况，在本研究中将其作为H⁃VGG⁃LSTM模型的研究对象.

表1 数据资料

Table 1 Description of dataset variables

	输入变量	单位
污染物变量	PM_2.5	μg·m^-3
	SO₂	μg·m^-3
	NO₂	μg·m^-3
	PM₁₀	μg·m^-3
	CO	μg·m^-3
	O₃	μg·m^-3
气象变量	风速	m·s^-1
	风向	°
	气温	℃
	湿度	%
	压强	hPa
	降水	mm

新窗口打开| 下载CSV

2 相关理论与模型构建

2.1　后向轨迹模型

后向轨迹模型可以计算简单的气团轨迹以及模拟复杂的扩散和沉积，其中混合单粒子拉格朗日综合轨迹模型（Hybrid Single⁃Particle Lagrangian Integrated Trajectory，HYSPLIT）是分析污染物远距离传输路径的模型，已被广泛地应用于大气污染跨地区传输和扩散的研究.

在后向轨迹模型计算原理的平流方程中采用线性插值方法，计算如式（1）和式（2）所示：

P^{' (t + Δ t)} = P (t) + V (p, t) Δ t

(1)

\begin{array}{l} P (t + Δ t) = \\ P (t) + 0.5 [V (p, t) + V (p^{'}, t + Δ t)] Δ t \end{array}

(2)

其中，积分时间步长需满足条件 $Δ t < \frac{0.75 格距}{U_{M A X}}$ ， $U_{M A X}$ 为最大风速.

垂直方向内插到地形跟随坐标系，如式（3）所示：

σ = \frac{Z_{t o p} - Z_{m s l}}{Z_{t o p} - Z_{g l}}

(3)

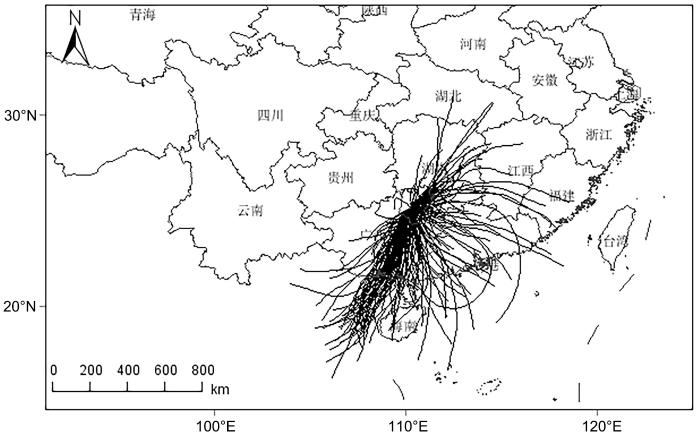
HYSPLIT模型将气象数据转化为轨迹矢量格式，计算后将轨迹线显示在指定区域可以得到桂林市四季后向气团轨迹模拟图.

2.2　卷积神经网络模型

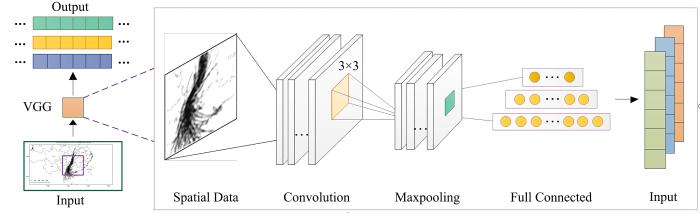
利用改进型卷积神经网络VGG模型提取气团轨迹线的特征，研究外部污染源对研究区空气质量的影响.多层非线性层可以增加网络深度以保证学习更复杂的模式.

VGG模型的卷积层对上层的小部分进行再分析，得到更加抽象的图像特征.卷积层如式（4）所示.将ReLU函数作为激活函数，可以有效避免梯度消失问题，数学表达如式（5）所示.

x_{j}^{l} = f (\sum_{i = M_{j}} x_{j}^{(l - 1)} \cdot k_{i} j^{l} + b_{j}^{l})

(4)

f (x) = m a x (0, x)

(5)

其中， $l$ 表示网络的第 $l$ 层， $M_{j}$ 表示上一层输出的感受野， $b$ 表示偏置， $k$ 为卷积层， $f (\cdot)$ 是非线性激活函数.

VGG模型中最大池化方法可以将输入特征的最大值输出，如式（6）所示：

x_{j}^{l} = f (β_{j}^{I} p (x_{j}^{I - 1}) + b_{j}^{l})

(6)

其中， $p (\cdot)$ 为池化函数， $β$ 为权重， $b$ 为偏置.

如图2所示，将HYSPLIT模型计算得到的气象轨迹图转化成224×224×3的图像格式作为VGG模型的图形化输入，提取气团的传输特征，最终获得空间图像转化而成的时序高维特征值；然后，将其与气象数据和其他污染物数据序列结合，构成混合深度学习模型的输入数据集.

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 VGG模型的体系结构

Fig.2 Architecture of the constructed VGG model

2.3　循环神经网络模型

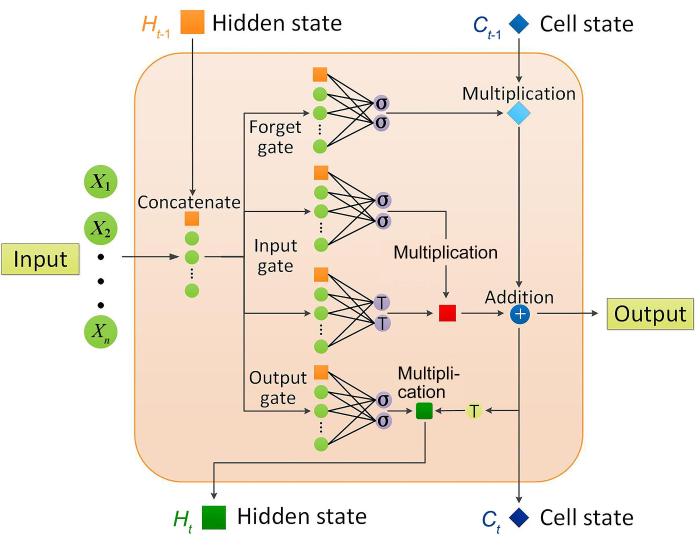
多元变量间的非线性映射关系可以用循环神经网络（Recurrent Neural Network，RNN）表示.LSTM是一种对普通RNN的改进型网络，其结构如图3所示.LSTM的输入和输出为持续的时间序列数据，其中输入数据由时序高维特征值、污染物和气象等数据组成，输出为目标污染物预测值.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 LSTM模型的体系结构

Fig.3 Architecture of the constructed LSTM model

LSTM节点通过门结构对细胞状态上的信息进行线性修改，保证在时间序列变长时时间相关性不会衰减.遗忘门以一定的概率控制上层隐藏的细胞状态，输入门处理当前时间点的输入，其计算分别如式（7）和式（8）所示：

f_{t} = σ (W_{f} \cdot [H_{t - 1}, X_{t}] + b_{f})

(7)

i_{t} = σ (W_{i} \cdot [H_{t - 1}, X_{t}] + b_{i})

(8)

输出门首先确定下一个隐藏状态的值 $H_{t}$ ，这包含之前输入的特征值、污染物及其影响因素信息，然后将隐藏状态作为当前神经元的输出 ${\hat{X}}_{t + 1}$ ，其计算如式（9）所示. ${\tilde{C}}_{t}$ 表示细胞更新后的状态，其计算如式（10）所示.细胞状态 $C_{t}$ 取决于前一层遗忘门和输入门的结果，如式（11）所示.

O_{t} = σ (W_{o} \cdot [H_{t - 1}, X_{t}] + b_{o})

(9)

{\tilde{C}}_{t} = t a n h (W_{c} \cdot [H_{t - 1}, X_{t}] + b_{c})

(10)

C_{t} = f_{t} \cdot C_{t - 1} + i_{t} \cdot {\tilde{C}}_{t}

(11)

其中， $X_{t}$ 为输入变量， $W_{f}$ ， $W_{i}$ ， $W_{o}$ 和 $W_{c}$ 分别为 $X_{t}$ 在遗忘门、输入门、输出门和细胞状态中的权重， $b_{f}$ ， $b_{i}$ ， $b_{o}$ 和 $b_{c}$ 分别是其偏移量.

2.4　H⁃VGG⁃LSTM模型构建

虽然区域内大气污染物浓度的变化过程存在一定的周期性，但由于其同时受到外部污染源和区域内部气象等因素的影响，所以表现出了非线性的变化过程.LSTM可以从时序序列数据中获得污染物及气象数据的历史依赖性，但缺乏对气象传输特征的考虑，未能有效解释大气污染传输机理.

VGG模型将HYSPLIT模型计算得到气团轨迹线模拟结果的时间序列数据，分段并进行卷积运算，然后提取其气团传输特征.但因其不能对整个时间序列进行有效提取，所以在大气污染的预测模型中，一般不单独使用VGG模型.

将HYSPLIT，VGG和LSTM模型融合得到H⁃VGG⁃LSTM模型，结构如图4所示.首先，运用HYSPLIT模型将气象数据转化为矢量格式进行计算，将轨迹线显示在指定区域，得到模拟的气团轨迹图；然后通过VGG模型从气团轨迹图中提取气团传输特征，将其与污染物和气象数据一同输入LSTM模型，得到目标污染物的预测浓度.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 H⁃VGG⁃LSTM的框架图

Fig.4 The framework of H⁃VGG⁃LSTM

3 实验分析

3.1　实验数据集

将PM_2.5作为预测指标.选择桂林市61个自动在线监测站点2017-2019年PM_2.5和气象小时级数据作为基准训练数据集.利用训练后的模型预测2020年2-5月的PM_2.5浓度.在输入模型之前，对观测数据进行预处理，利用Min⁃Max方法对输入数据进行归一化，以提高模型的训练速度和预测精度.Min⁃Max的归一化过程如式（12）所示：

z = \frac{x - m i n (x)}{m a x (x) - m i n (x)}

(12)

其中， $x$ 为监测数据， $m i n (x)$ 和 $m a x (x)$ 分别为监测数据的最大值和最小值， $z$ 为归一化后的值.

3.2　气团模拟和聚类分析

模拟时间尺度为2017年7月1日-2019年6月30日桂林市外来气团的1000 m高度后向轨迹分布，并结合聚类分析法对桂林市PM_2.5气团轨迹和潜在污染源区进行分析得到气团轨迹图.以2017年春季为例，得到模拟结果如图5所示.由图可见，桂林市后向气团轨迹分布的季节变化特征显著，对比图1，气团轨迹的走向与“湘桂走廊”方向基本一致.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 对2017年春季桂林市后向气团轨迹的模拟结果

Fig.5 Simulation results of backward air mass trajectory in Guilin in spring of 2017

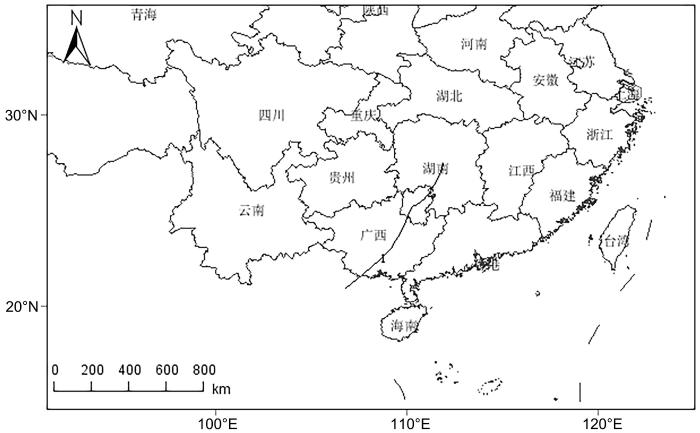
采用聚类方式对轨迹线进行聚类，得到各季节具有代表性的轨迹线，以2017年春季为例，结果如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 对2017年春季桂林市气团轨迹线的聚类结果

Fig.6 Clustering results of backward air mass trajectory lines in Guilin in spring of 2017

3.3　网络模型参数

模型的超参数有神经元数量及Time_step.

表2给出了神经元数量对H⁃VGG⁃LSTM模型性能的影响，由表可见，神经元为32时模型的综合预测性能最佳.

表2 神经元数量对H⁃VGG⁃LSTM模型性能的影响

Table 2 Effect of the number of neuron nodes on the performence of H⁃VGG⁃LSTM

Neurons	RMSE	MAE
16	0.941	0.756
32	0.584	0.523
64	0.763	0.654
128	0.836	0.736

新窗口打开| 下载CSV

表3是Time_step对H⁃VGG⁃LSTM模型性能的影响，由表可见， $T i m e_s t e p = 10$ 时模型效率最高.因此，设置 $T i m e_s t e p = 10$ ，即利用过去10 h的浓度数据，预测下一小时的污染物浓度.

表3 Time_step对H⁃VGG⁃LSTM模型性能的影响

Table 3 Effect of Time_step on the performence of H⁃VGG⁃LSTM

Time_step	RMSE	MAE
4	0.756	0.658
6	0.523	0.502
8	0.489	0.433
10	0.328	0.303
12	0.459	0.412
14	0.602	0.598

新窗口打开| 下载CSV

3.4　评价方法

对提出的H⁃VGG⁃LSTM模型的性能进行了评估.首先，将H⁃VGG⁃LSTM模型与传统预测模型进行比较，包括基于统计理论的自回归移动平均模型（Autoregressive Integrated Moving Average Model，ARIMA）、基于地理要素变量的土地利用回归模型（Land Use Regression，LUR）、门控循环单元（Gate Recurrent Unit，GRU）、基于注意力机制的并行网络（Attention⁃based Parallel network，APNet）、基于注意力机制的LSTM密集连接卷积网络（Densely Connected Convolutional Networks with Attention⁃Based LSTM，DCCN⁃ALSTM）.

利用均方根误差（Root Mean Squared Error，RMSE）、平均绝对误差（Mean Absolute Error，MAE）和对称平均绝对百分比误差（Symmetric Mean Absolute Percentage Error，SMAPE）三个评价指标对H⁃VGG⁃LSTM模型的预测性能进行评价.

3.5　模型性能

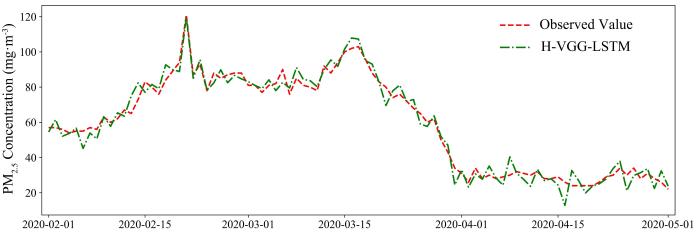
经过训练收敛得到H⁃VGG⁃LSTM的最优权重，使用测试集评估，得到PM_2.5的预测值与实际值，如图7所示．由图可见，模型预测的PM_2.5浓度值与实际值的拟合效果较好.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 H⁃VGG⁃LSTM模型对PM_2.5浓度的预测结果

Fig.7 Prediction results of PM_2.5 by H⁃VGG⁃LSTM model

比较H⁃VGG⁃LSTM模型与ARIMA，LUR，GRU，APNet和DCCN⁃ALSTM的预测表现.表4给出各模型RMSE，MAE和SMAPE的计算值.

表4 六种模型的预测表现

Table 4 Prediction performance of six models

Method	RMSE	MAE	SMAPE
ARIMA	0.424	0.368	5.01%
LUR	0.350	0.319	4.34%
GRU	0.292	0.243	3.28%
APNet	0.251	0.225	2.21%
DCCN⁃ALSTM	0.235	0.216	2.16%
H⁃VGG⁃LSTM	0.202	0.198	1.97%

新窗口打开| 下载CSV

ARIMA的预测精度较差，因为这种模型仅适用于平稳的时间序列数据，而桂林市复杂的大气环境导致其污染物浓度及气象状况波动较大.LUR可以结合土地利用特征，其预测精度和只考虑单一内生变量的ARIMA相比，有较大的提高.GRU可以获得时序数据中的长期依赖关系，能够大概拟合较长时间域的真实监测数据.与其他模型相比，H⁃VGG⁃LSTM获得了最好的预测结果，其三项评价指标在比较实验中全部取得最低值，其中，RMSE比APNet和DCCN⁃ALSTM分别低19.5%和14.0%.

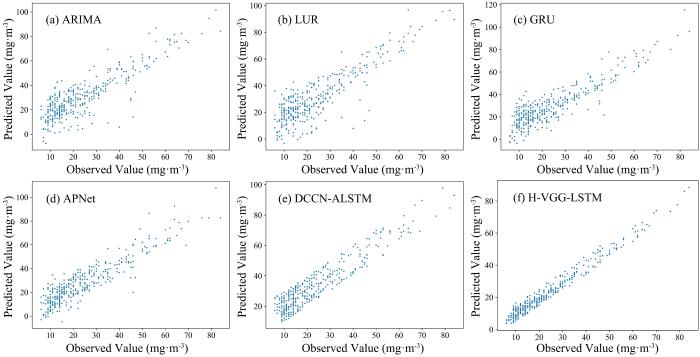
为了直观地展示预测的效果，图8对比了H⁃VGG⁃LSTM和五个参照模型对PM_2.5观测和预测的散点图.各模型的预测曲线与观测曲线的趋势一致，且均呈线性相关.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 六种模型对PM_2.5浓度预测结果的散点分布图

Fig.8 Scatter plots of the prediction results of PM_2.5 by six models

由图可见，ARIMA和LUR的预测值和实际观测值之间的分布误差较大，GRU的分布误差比ARIMA小，表明深度学习模型在捕捉时序数据特征方面具有优势.在某些极值处的预测，APNet产生了较大的误差.应用注意力机制考虑了空间特征的DCCN⁃ALSTM模型表现较好，但其对预测地区的数据平稳性要求较高，因而模型的泛化能力较弱.与上述模型相比，基于深度学习和物理机理的H⁃VGG⁃LSTM在桂林地区的PM_2.5浓度预测上有最好的效果，其VGG和LSTM的混合结构充分考虑了与目标参数相关的线性、非线性和非泛函关系，有效地提取了目标参数.该模型通过CNN准确捕捉输入数据的潜在内在特征，通过LSTM既可以充分反映时间序列的短期时间特征，捕捉短期时序突变点，也可以识别时间序列的长期依赖特征，进一步提高预测精度.

3.6　消融实验

3.6.1　消融实验方法

时序高维气象传输特征值由气团轨迹数据经HYSPLIT和VGG组合得到，为进一步探究H⁃VGG⁃LSTM模型中气团轨迹数据的影响，针对该模型设计了消融实验，使用以下模型结构在相同的数据集中进行实验.模型的结构组成见表5.

表5 两种模型的结构组成

Table 5 Structure of the two models

	HYSPLIT	VGG	LSTM
M1			√
M2	√	√	√

新窗口打开| 下载CSV

（1）M1模型：未加入HYSPLIT模型和VGG模型，LSTM的输入数据中只有气象数据和污染物数据，未考虑时序高维气象传输特征值.

（2）M2模型：即本文提出的基于后向气团轨迹的大气污染特征时序混合模型H⁃VGG⁃LSTM，利用HYSPLIT和VGG得到时序高维气象传输特征值，结合气象和其他污染物时序数据构成LSTM的输入数据.

3.6.2　消融实验结果及分析

将3.5.1中的M1和M2两种模型在3.1中的数据集上进行了消融实验，实验结果如表6所示.

表6 两种模型在3.1的数据集上进行消融实验的结果

Table 6 Results of the ablation experiment by two models on datasets in 3.1

	RMSE	MAE	SMAPE
M1	0.329	0.362	3.61%
M2	0.201	0.197	1.98%

新窗口打开| 下载CSV

由表可见，M1与M2模型在相同数据集上的实验结果有一定差距，M2的RMSE，MAE和SMAPE比M1分别低0.128，0.165和1.63%，这是由于M2模型中LSTM的输入数据集中加入了HYSPLIT和VGG组合得到污染物传输的时序高维特征值，模型整体考虑了污染物传输的空间特征信息，提高了对目标污染物的预测精度.

4 结论

本文提出一种基于后向气团轨迹的大气污染特征时序混合模型，通过HYSPLIT得到后向气团轨迹时序模拟图，输入VGG提取气团轨迹的传输特征时序数据，将其与气象和污染物数据结合，输入LSTM得到对目标污染物的预测数据.在实验部分对提出模型的性能进行了评估，并将其与物理模型、传统的机器学习模型和深度学习模型进行了比较.结果表明，H⁃VGG⁃LSTM的RMSE，MAE和SMAPE指标均优于现有的其他先进方法.该模型充分考虑了污染物扩散的时间和空间特征，有效提高了气象复杂地区的大气污染物的预测精度，可为区域大气质量控制和研究大气污染机理提供较大的帮助.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Yin

Z C

， Wang

H J

， Liao

，et al.

Seasonal to interannual prediction of air pollution in China：Review and insight

Atmospheric and Oceanic Science Letters，2022，15(1)：100131.