聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用.
传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力.
以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好.
同时,引入范数对矩阵进行稀疏约束来发展一些稳健的NMF算法.Peng et al[31 ] 提出一种基于相关熵的鲁棒非负矩阵分解算法(l 1 ⁃Norm Non⁃Negative Matrix Factorization Based on Maximum Correntropy Criterion,l 1 ⁃CNMF),将传统的NMF算法与l 1 ⁃范数和最大相关熵准则结合,对系数矩阵进行稀疏约束,在图像聚类任务中取得了较好的效果.Zhang et al[32 ] 提出基于l 2,1 ⁃范数的矩阵分解来获得抗噪声和离群点的鲁棒解.Chen et al[33 ] 提出基于流形正则化和稀疏学习的鲁棒非负矩阵分解算法(Robust Non⁃Negative Matrix Factorization via Jointly Manifold Regularization and Sparse Learning,MS⁃RNMF),在NMF中引入l 2,1 ⁃范数约束,同时对基矩阵和系数矩阵进行稀疏约束.
然而,传统的基于NMF的聚类算法仍然具有以下问题:(1)容易受非高斯噪声和异常值的影响而产生较大的误差;(2)无法充分利用数据的结构信息;(3)没有利用矩阵的稀疏性,导致计算复杂,优化时间长.
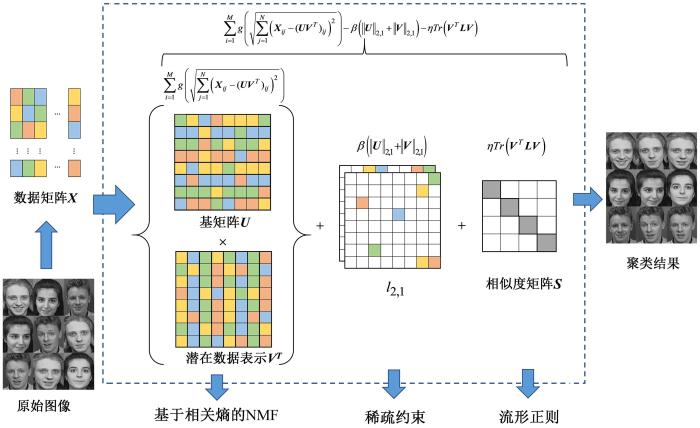
受上述工作启发,为了充分保持数据的结构信息并继承传统NMF算法的优点,本文提出基于相关熵和流形正则化的图像聚类算法 (CRNMF).在提出的框架中引入相关熵代替欧式距离来减轻非高斯噪声的影响.另外,充分考虑数据的结构信息并通过l 2,1 ⁃范数进行稀疏约束,减轻异常值的影响.CRNMF算法的流程如图1 所示.
(1)针对图像聚类问题,提出一个基于相关熵和流形正则化的联合优化框架CRNMF,将相关熵、稀疏约束和流形正则整合到一个统一的目标函数中.
(2)通过相关熵代替欧式距离,通过流形正则化保存数据的局部结构,并引入l 2,1 ⁃范数对非负矩阵进行稀疏约束,增强了算法的抗非高斯噪声能力和局部平滑性.
(3)利用半二次优化技术(Half⁃Quadratic Optimization Technique,HQ)对CRNMF进行优化,将非凸目标函数转化为乘法形式的二次函数,导出算法的更新规则,同时在理论上证明了算法的收敛性,并分析了计算复杂度.
图1
图1
CRNMF框架
Fig.1
The framework of CRNMF
(4)在五个图像数据集上进行实验,实验结果表明,提出的算法在图像聚类任务中有较好的有效性和鲁棒性.
1 相关工作
1.1 非负矩阵分解 (NMF)
NMF的主要思想是将非负数据矩阵近似分解为两个低维非负矩阵,其乘积尽可能逼近原数据矩阵以找到原始数据矩阵的恰当低维表示.
假设X = x 1 , x 2 , … , x N ∈ ℝ ≥ 0 M × N X M [3 ] 可以表示为:
X ≈ U V T (1)
其中,K < m i n N , M U = u i k ∈ ℝ ≥ 0 M × K V = v j k ∈ ℝ ≥ 0 N × K
多数情况下,传统的NMF通常使用欧式距离作为度量,表示为以下优化问题:
𝒪 S E D = ∑ j = 1 N ∑ i = 1 M X i j - U V T i j 2 = X - U V T F 2 (2)
其中,⋅ F ⋅ T
虽然U V 式(2)中是非凸的,但不是同时非凸.因此,传统NMF的乘法更新规则如下:
U ← U X V U V T V (3)
V ← V X T U V U T U (4)
实际上,通常K ≪ M K ≪ N . 因此,NMF基本上为寻找原始数据矩阵的压缩近似.近似值按列查看如下所示:
x j ≈ ∑ k = 1 K u k v j k (5)
其中, u k U k 列向量.因此,数据向量 x j U V
与其他矩阵分解算法最大的不同是,NMF对U V [19 ] .
1.2 流形正则化
在许多现实世界的应用中,数据点常位于一个低维的流形上,因此流形学习引起了巨大的关注.通常,邻近的数据点可能有相似的特征并被分类或划分到同一组中.假设邻近的数据点在新的数据空间中也是相近的,称为“流形假设”[34 ] .将“流形假设”引入非负矩阵分解中,即局部流形学习,以期望小邻域内的邻近数据点可以共享内在的几何结构.
为了捕捉数据的内在几何结构使用基于图的流形方法,使用热核函数构建最近邻图来度量数据点之间的相似度.若两个数据点在原始空间中相似则在目标空间中也相似.给定具有N X = x 1 , x 2 , … , x N S ∈ ℝ N × N
S = e - x i - x j 2 2 λ 2 , i 与 j 相 邻 0 , 否 则 (6)
为了保留局部信息,结合流形正则化和局部相似度使数据点达到无差异[33 ] .vi 和vj 是与数据点xi ,xj 关联的特征向量.通过1 2 m i n ∑ i , j v i - v j 2 vi 和vj 之间的微小差异.因此,局部相似度得分越高则数据点之间的差异越小,定义如下:
𝒪 d a t a = ∑ i , j = 1 N d v i , v j × S = T r V T D V - T r V T S V = T r V T L V (7)
其中,T r ⋅ D = ∑ j = 1 N S L ∈ ℝ N × N L = D - S .
1.3 相关熵
由于对非高斯噪声和异常值的鲁棒性,相关熵已被广泛应用.作为一个非线性和局部相似性度量函数,相关熵直接与相似随机变量A 和B 在联合空间邻域中的概率有关,定义如下[28 ,35 -36 ] :
V A , B = E κ A , B = ∫ κ a , b d F A B a , b (8)
其中,E ⋅ κ ⋅ , ⋅ F A B a , b A , B κ ⋅ , ⋅
κ σ a , b = g a , b = e - a - b 2 2 σ 2 (9)
其中,σ > 0 F A B a , b a n , b n n = 1 N
V ̂ N , σ A , B = 1 N ∑ n = 1 N g a n - b n (10)
从两个不同的方面进行分析来说明相关熵的鲁棒性.首先,可以利用高斯核的泰勒级数展开重写式(8):
V A , B = ∑ n = 0 ∞ - 1 n 2 n σ 2 n n ! ∫ ∫ a - b 2 n d F A B a , b (11)
从统计学角度看,相关熵可以捕捉高阶矩(即所有的偶数阶矩),这有助于抑制非高斯噪声和异常值的负面影响.其次,每个数据样本对相关熵的贡献在很大程度上取决于沿联合空间中a = b l 2 ⁃范数距离;如果样本点相距较远,则相关熵表现为l 1 ⁃范数距离;如果样本点相距非常远,则相关熵表现为l 0 ⁃范数.因此,基于上述分析,相关熵对非高斯噪声和异常值不敏感.
1.4 半二次优化技术(HQ)
通常,基于信息论学习(Information Theoretic Learning,ITL)方法的目标函数是非线性的且非凸的,难以直接进行优化.幸运的是,HQ常被用来解决基于ITL的优化问题[30 -31 ,36 ] .假设ϕ e e ∈ ℝ M
ϕ e = ∑ i = 1 M ϕ e i (12)
其中,ei 是向量 e i 个元素.基于最小化的HQ,通过引入辅助变量ϱ i ei ,方法如下:
ϕ e i = m i n ϱ i Q e i , ϱ i + φ ϱ i (13)
其中,ϱ i ϕ ⋅ Q e i , ϱ i
φ ⋅ ϕ ⋅ Q e i , ϱ i
Q e i , ϱ i = 1 2 ϱ i e i 2 (14)
假设Q e , ϱ = ∑ i = 1 M Q e i , ϱ i ϱ = ϱ 1 , ⋯ , ϱ M . 结合式(13)和式(14),可以得到式(13)的向量形式如下:
ϕ e = m i n ϱ Q e , ϱ + ∑ i = 1 M φ ϱ i (15)
2 CRNMF算法
2.1 目标函数
如前所述,为了克服传统NMF算法的局限性,学习有区别的数据表示,充分利用数据的结构信息,增强矩阵的稀疏性,本文提出基于相关熵和流形正则化的CRNMF框架.CRNMF用相关熵代替欧式距离,通过流形正则化学习局部结构,并引入l 2,1 ⁃范数对非负矩阵进行约束,有效减轻了非高斯噪声和异常值的影响,具有良好的有效性和鲁棒性.
m a x U , V 𝒪 = ∑ i = 1 M g ∑ j = 1 N X i j - U V T i j 2 - β U 2,1 + V 2,1 - η T r V T L V (16)
其中,第一项为用相关熵代替欧式距离,第二项是对聚类中心U V β η
2.2 算法优化
显然,上述目标函数(16)的优化问题很难直接解决,因为目标函数(16)中的U V [37 ] ,因此,本文使用基于共轭函数理论的HQ对CRNMF进行优化.首先将非凸目标函数转化为乘法形式的二次函数,然后利用乘法更新规则对转化后的二次函数进行求解.基于凸共轭函数的性质,有以下命题:
g x = m a x ϱ ϱ x 2 σ 2 - φ ϱ (17)
其中,ϱ x ,ϱ ϱ = - g x .
显然,CRNMF的优化问题(16)可以通过使用命题1进行优化:
m a x U , V , ϱ 𝒪 ̂ = ∑ i = 1 M ϱ i σ 2 ∑ j = 1 N X i j - U V T i j 2 - φ ϱ i - β U 2,1 + V 2,1 - η T r V T L V (18)
其中,𝒪 ̂ 𝒪 ϱ = ϱ 1 , ⋯ , ϱ M T U V 𝒪 ̂ ϱ i
ϱ i = - g ∑ j = 1 N X i j - U V T i j 2 = - e - ∑ j = 1 N X i j - U V T i j 2 2 σ 2 (19)
由于应用的多样性,没有一个统一的策略来选择最佳的核带宽参数σ . 因此,σ σ
σ = 1 2 M ∑ i = 1 M ∑ j = 1 N X i j - U V T i j 2 (20)
m a x U , V 𝒪 ̂ = ∑ i = 1 M ϱ i ∑ j = 1 N X i j - U V T i j 2 - β U 2,1 + V 2,1 - η T r V T L V (21)
m i n U , V 𝒪 ̂ 1 = - ∑ i = 1 M ϱ i ∑ j = 1 N X i j - U V T i j 2 + β U 2,1 + V 2,1 + η T r V T L V = T r X T H X - 2 V U T H X + V U T H U V T + β T r U M 1 U T + V M 2 V T + η T r V T L V (22)
H i i = - ϱ i = e - ∑ j = 1 N X i j - U V T i j 2 2 σ 2 (23)
M 1 i i = 1 U i , i = 1,2 , ⋯ , M (24)
M 2 j j = 1 V j , j = 1,2 , ⋯ , N (25)
假设Φ = Φ i k ∈ ℝ ≥ 0 M × K Ψ = Ψ j k ∈ ℝ ≥ 0 N × K U V U ≥ 0 V ≥ 0
ℒ = T r X T H X - 2 V U T H X + V U T H U V T + β T r U M 1 U T + V M 2 V T + η T r V T L V + T r Φ U T + T r Ψ V T (26)
∂ ℒ ∂ U = - 2 H X V + 2 H U V T V + 2 β M 1 U + Φ (27)
使用KKT条件Φ i k u i k = 0
u i k ← u i k H X V i k H U V T V + β M 1 U i k (28)
∂ ℒ ∂ V = - 2 X T H U + 2 V U T H U + 2 β M 2 V + 2 η L V + Ψ (29)
使用KKT条件Ψ j k v j k = 0
v j k ← v j k X T H U + η S V j k V U T H U + β M 2 V + η D V j k (30)
输入:数据矩阵X p β η K T .
4.根据式(24)和式(25)分别计算对角矩阵M 1 , M 2
3 算法分析
3.1 收敛性分析
不失一般性,使用辅助函数法证明提出算法的收敛性,并有以下定理:
CRNMF中的目标函数𝒪 ̂ 1
在证明定理1之前,首先给出辅助函数和引理1的定义如下:
G v , v ' ≥ F v , G v , v = F v (31)
如果G F F t t + 1
v t + 1 = a r g m i n V G v , v t (32)
F v t + 1 ≤ G v t + 1 , v t ≤ G v t , v t = F v t
显然,如果使用引理1和更新规则(28)和(30)证明最小化目标函数𝒪 ̂ 1 G 𝒪 ̂ 1 u i k v j k U V F i k F j k u i k v j k U V
F i k ' = ∂ 𝒪 ̂ 1 ∂ U i k = - 2 H X V + 2 H U V T V i k + 2 β M 1 U i k (33)
F i k ' ' = ∂ 2 𝒪 ̂ 1 ∂ U 2 i k = 2 H i i V T V k k + 2 β M 1 i i (34)
F j k ' = ∂ 𝒪 ̂ 1 ∂ V j k = - 2 X T H U + 2 V U T H U j k + 2 β M 2 V j k + 2 η L V j k (35)
F j k ' ' = ∂ 2 𝒪 ̂ 1 ∂ V 2 j k = 2 U T H U k k + 2 β M 2 j j + 2 η L j j (36)
本质上,更新规则是元素式的.因此,需要证明F i k F j k
G u , u i k t G v , v j k t F i k F j k
G u , u i k t = F i k u i k t + F i k ' u - u i k t + H U V T V + β M 1 U i k u i k t u - u i k t 2 (37)
G v , v j k t = F j k v j k t + F j k ' v - v j k t + V U T H U + β M 2 V + η D V j k v j k t v - v j k t 2 (38)
显然,G u , u = F i k u G v , v = F j k v G u , u i k t ≥ F i k u G v , v j k t ≥ F j k v . 结合式(33)和式(34),将F i k u
F i k u = F i k u i k t + F i k ' u i k t u - u i k t + 1 2 F i k ' ' u i k t u - u i k t 2 = F i k u i k t + F i k ' u i k t u - u i k t + u - u i k t 2 H i i V T V k k + β M 1 i i (39)
为了保证G u , u i k t ≥ F i k u 式(37)和式(39),得到以下不等式:
H U V T V + β M 1 U i k u i k t ≥ H i i V T V k k + β M 1 i i (40)
H U V T V i k = ∑ l = 1 K u i l t H i i V T V l k ≥ u i k t H i i V T V k k (41)
结合式(35)和式(36),将F j k v
F j k v = F j k v j k t + F j k ' v j k t v - v j k t + 1 2 F j k ' ' v j k t v - v j k t 2 = F j k v j k t + F j k ' v j k t v - v j k t + v - v j k t 2 U T H U k k + β M 2 j j + η L j j (42)
为了保证G v , v j k t ≥ F j k v 式(38)和式(42),得到以下不等式:
V U T H U + β M 2 V + η D V j k v j k t ≥ U T H U k k + β M 2 j j + η L j j (43)
V U T H U j k = ∑ l = 1 K v j l t U T H U l k ≥ v j k t U T H U k k (44)
η D V j k = η ∑ l = 1 N D j l v l k t ≥ η D j j v j k t ≥ η D - S j j v j k t = η L j j v j k t (45)
对于目标函数𝒪 ̂ 1 G u , u i k t 式(37),将G v , v j k t 式(38),导出以下更新规则:
u i k t + 1 = u i k t - u i k t F i k ' u i k t 2 H U V T V + β M 1 U i k = u i k t H X V i k H U V T V + β M 1 U i k (46)
v j k t + 1 = v j k t - v j k t F j k ' v j k t 2 V U T H U + β M 2 V + η D V j k = v j k X T H U + η S V j k V U T H U + β M 2 V + η D V j k (47)
3.2 鲁棒性分析
本文通过HQ对CRNMF算法进行优化,将非凸优化问题转化为迭代加权的NMF问题.由命题1可知,当固定矩阵U V X
ϱ i = - g ∑ j = 1 N X i j - ( U V T ) i j 2 = - e - ∑ j = 1 N X i j - U V T i j 2 2 σ 2 (48)
根据式(48)可知,当数据受损严重时将被分配较小的权重,因而对目标函数的贡献较小.通过引入相关熵和l 2,1 ⁃范数,CRNMF能够有效地减轻噪声对聚类结果的影响.因此,CRNMF算法对噪声和异常值不敏感.
3.3 计算复杂度分析
计算复杂度对于评估算法的效率非常重要.分析每次更新迭代的CRNMF计算成本,并使用最常用的符号O 式(6)可知,CRNMF需要O M N 2 p⁃ 近邻图来计算相似度矩阵,M 为特征维度,N 为样本数量.此外,根据式(20)、式(23)、式(28)和式(30)更新σ H U V O T M N K K 为嵌入维度.假设提出的算法在T O M N 2 + T M N K .
4 实验
4.1 实验设置
4.1.1 实验环境
所有算法均用Matlab R2018a实现,在一台2.40 GHz Intel Core CPU 16.0 GB RAM和Windows 10操作系统的计算机上进行.
4.1.2 数据集
实验使用五个图像数据集,分别为CMU PIE,ORL,UMIST,YaleB和COIL20.用于聚类任务的数据集的详细特征如表2 所示,图2 至图6 给出了每个数据集的图像样本.对于每个图像数据集,将数据格式化为具有相同维数和样本数大小的数据矩阵,并将每个样本(即数据矩阵的每一列)归一化为欧几里得长度.
CMU PIE:包含68个人的2856幅图像,每个人有13种不同的姿态、4种不同表情和43种不同的光照条件.
ORL:剑桥大学提出的数据集,包含40个人的400幅图像.每个人有10张面部表情图像.
UMIST:包含20个人的575幅图像,每个主题由不同种族、性别或外貌的图像组成,并包含从侧面到正面的一系列姿势.
YaleB:包含38个人的2414幅正面人脸图像(大约每人64幅图像),所有图像都已损坏.
COIL20:哥伦比亚大学提出的数据集,包含20个对象的1440幅图像,每个对象都由72幅不同角度的图像组成.
图2
图2
CMU PIE数据集样本
Fig.2
Samples of CMU PIE dataset
图3
图3
ORL数据集样本
Fig.3
Samples of ORL dataset
图4
图4
UMIST数据集样本
Fig.4
Samples of UMIST dataset
图5
图5
YaleB数据集样本
Fig.5
Samples of YaleB dataset
图6
图6
COIL20数据集样本
Fig.6
Samples of COIL20 dataset
4.1.3 评价指标
为了衡量聚类性能,采用三个常用的评价指标,即聚类精度(ACC )、归一化互信息(NMI )和纯度(PUR ).
A C C = ∑ N n = 1 δ r n , m a p c n N (49)
其中,N r n c n δ h , z δ
h = z δ m a p ⋅ [38 ] 将每个聚类标签映射到来自数据集的等价标签的映射函数.
N M I = ∑ N i = 1 ∑ N j = 1 n i , j l g n i , j n i n j ∑ N i = 1 n i l g n i n ∑ N j = 1 n ̂ j l g n j n (50)
其中,n i n ̂ j i j n i , j N
P U R = 1 n ∑ N i = 1 m a x n i j (51)
具体地,聚类精度(ACC )计算聚类中的数据点来自同一类的百分比;归一化互信息(NMI )衡量不同簇的相似性;纯度(PUR )衡量聚类中的数据点来自一个类的程度.所有评价指标范围是0到1,值越大,聚类性能越好.
4.1.4 比较算法
为了证明提出的CRNMF算法在聚类任务中的有效性和鲁棒性,将CRNMF与七种相关聚类算法进行比较,它们是k⁃ means,NMF,GNMF[19 ] ,CGNMF[25 ] ,GDNMF[24 ] ,GLoRSS[28 和l 1 ⁃CNMF[31 ] .在这些比较算法中,k⁃ means是基线.
(1)k⁃ means算法是应用最广泛的聚类算法之一,常被用于聚类算法的基线.
(2)非负矩阵分解(NMF)将原始数据矩阵分解为两个非负矩阵,实现了高维数据的低维表示,以更好地应用于聚类任务.
(3)图正则化非负矩阵分解(GNMF)通过结合拉普拉斯正则化来考虑流形数据上的固有几何结构.
(4)基于相关熵诱导度量的图正则化非负矩阵分解算法(CGNMF)将相关熵引入GNMF,在保持数据几何结构的同时增强算法的抗噪声能力.
(5)基于图的带标签信息的判别非负矩阵分解(GDNMF)是在考虑了数据的局部几何结构的同时,在NMF中引入了标签信息.
(6)GLoRSS是一种基于最大相关熵准则的鲁棒子空间学习算法.
(7)l 1 ⁃CNMF是基于最大相关熵准则的l 1 ⁃范数非负矩阵分解算法,该算法用相关熵提高鲁棒性并且对系数矩阵进行l 1 ⁃范数约束.
4.1.5 其他设置
实验需要预先设置四个主要参数,分别是图最近邻数p β η K . 在不提及其他方面的情况下,将参数p β η 5,0.1,100 K λ σ 式(20)计算.GNMF算法的正则化参数设置为100.CGNMF算法的正则化参数设置为10-6 .GDNMF算法的正则化参数设置为1,标签约束参数在1,5 , 10,100 0.001 ,
0.01,0.1,1 , 10,100 l 1 ⁃CNMF算法的稀疏参数设置为0.1.与直接应用于原始数据的
k ⁃means不同,其他算法的聚类过程包括两个主要步骤:(1)获得原始数据矩阵的潜在低维表示矩阵;(2)对学习的表示矩阵运用k⁃ means算法.根据经验,最大迭代次数设置为300次,并对所有算法进行20次具有不同初始值的相关蒙特卡罗方法.对于每个数据集,计算出平均结果作为所有算法的最终聚类结果,并突出显示最佳结果.
4.2 聚类结果
在五个图像数据集上的实验结果如表3 所示,表中粗体字为结果最优.可以看出,提出的CRNMF算法基本在所有图像数据集上都获得了最佳的聚类性能,在大多数情况下,CRNMF在精度(ACC )、归一化互信息(NMI )和纯度(PUR )上优于其他算法.例如,在五个图像数据集上,CRNMF的聚类性能比GNMF有明显提高,可以证明相关熵的有效性.在CMU PIE数据集上,CRNMF的聚类精度(ACC )、归一化互信息(NMI )和纯度(PUR )比CGNMF分别提高1.94%,3.95%和0.54%,证明增加稀疏约束在一定程度上可以提高聚类结果.
在所有数据集上,CRNMF的聚类结果均优于l 1 ⁃CNMF,证明利用l 2,1 ⁃范数对矩阵约束的有效性.与传统的聚类算法相比,CRNMF在大多数情况下优于这些比较算法的主要原因可以概括如下:该算法在目标函数中使用相关熵代替欧式距离,可以减少非高斯噪声污染对数据集的负面影响;CRNMF还充分考虑了数据的局部结构,并通过l 2,1 ⁃范数对矩阵进行稀疏约束,在保持局部平滑的同时充分利用了矩阵的稀疏性,因此具有更好的聚类效果.此外,k⁃ means的聚类结果比其他算法差得多,表明挖掘数据潜在的低维表示可以提高聚类任务的性能.
同时,为了验证CRNMF各部分的有效性,分别将β η β = 0 A C C = 75.56 % η = 0 A C C = 19.64 %
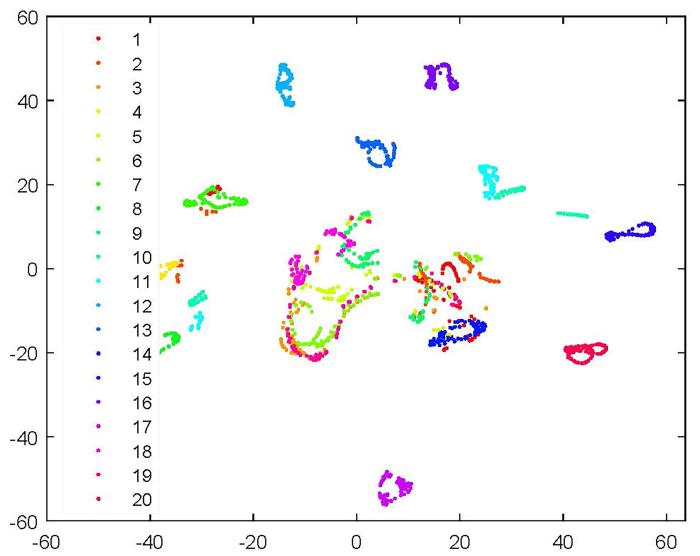
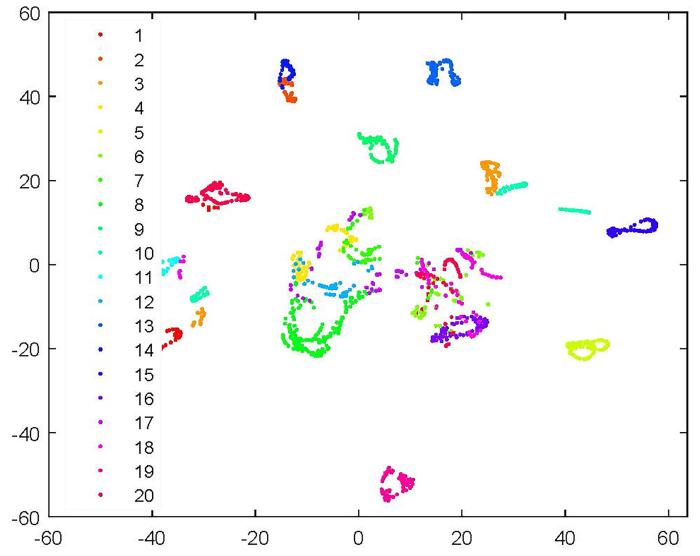
CRNMF在COIL20数据集上的T⁃SNE可视化结果如图7 和图8 所示,由图可见,CRNMF可以将相似的数据聚集到同一类中.
4.3 鲁棒性
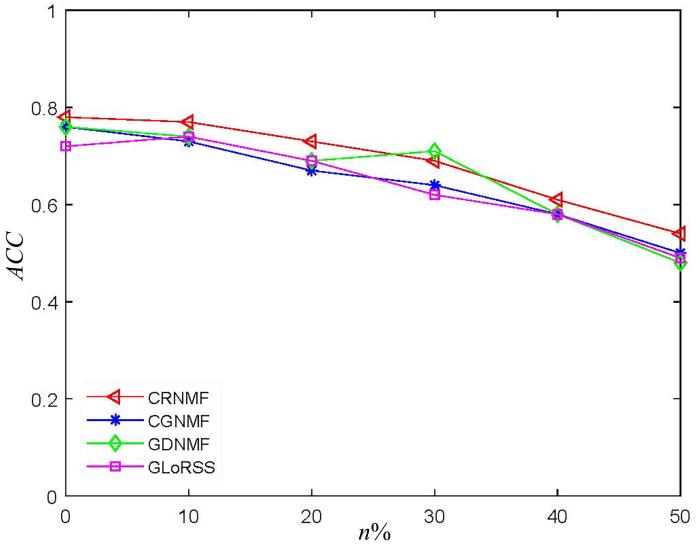
为了验证CRNMF算法的鲁棒性,在CMU PIE数据集上进行实验.具体地,将噪声密度为0.01的椒盐噪声加入CMU PIE数据集.CMU PIE数据集加入椒盐噪声后的图像如图9 所示.CMU PIE数据集加入椒盐噪声后聚类精度的变化如图10 所示,其中,n %表示所有图像的噪声百分比,n =0,10,20,30,40,50,n 越大,噪声水平越高.由图可见,随着噪声水平的增加,提出的CRNMF算法在大多数情况下具有最佳的聚类精度,表明相关熵对非高斯噪声和异常值不敏感,所以处理非高斯噪声和异常值是有效的.与实验中的其他算法相比,CRNMF算法在具有明显异常值的CMU PIE数据集上鲁棒性更强.
图7
图7
COIL20数据集T⁃SNE可视化
Fig.7
T⁃SNE visualization of COIL20 dataset
图8
图8
CRNMF在COIL20数据集上的T⁃SNE可视化
Fig.8
T⁃SNE visualization of CRNMF on COIL20 dataset
图9
图9
加入椒盐噪声的CMU PIE数据集
Fig.9
CMU PIE dataset with salt and pepper noise
图10
图10
CMU PIE数据集上椒盐噪声影响下的聚类精度变化
Fig.10
Variation of ACC under the influence of salt and pepper noise on CMU PIE dataset
4.4 参数选择
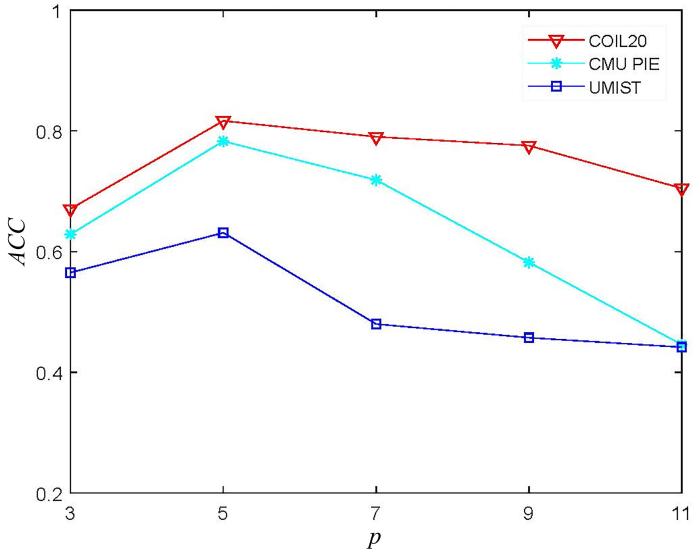
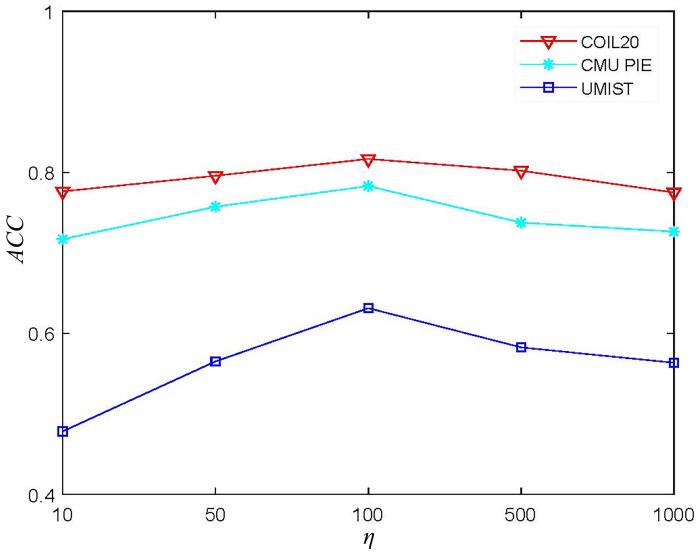
在COIL20,CMU PIE和UMIST数据集上研究参数p β η p β η 3,5 , 7,9 ,
11 0.01,0.1,1 , 10,100 10,50,100,500 ,
1000 . 图11 至图13 显示了参数p β η p p = 5 p p = 5 0.01,0.1,1 , 10,100 β β = 0.1 β η
4.5 收敛性
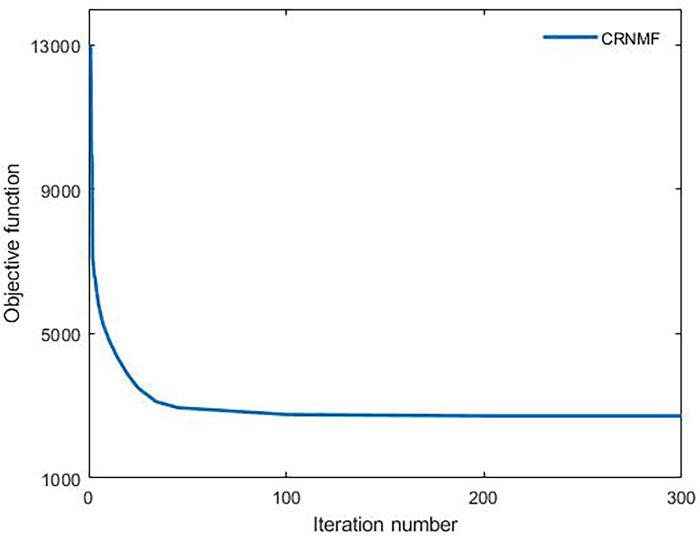
为了验证CRNMF的收敛性,在COIL20数据集上进行实验.实验结果如图14 所示,x 轴表示迭代次数,y 轴表示CRNMF的目标函数值𝒪 ̂ 1 . 由图可见,对于COIL20数据集,在乘法更新规则(28)和(30)下,𝒪 ̂ 1
图11
图11
在COIL20,CMU PIE和UMIST数据集上CRNMF随参数p
Fig.11
ACC of CRNMF with the change of parameter p
图12
图12
在COIL20,CMU PIE和UMIST数据集上CRNMF随参数β
Fig.12
ACC of CRNMF with the change of parameter β
图13
图13
在COIL20,CMU PIE和UMIST数据集上CRNMF随参数η
Fig.13
ACC of CRNMF with the change of parameter η
图14
图14
CRNMF在COIL20数据集上的收敛曲线
Fig.14
Convergence curves of CSNMF on COIL20 dataset
5 结论和展望
本文提出一种基于相关熵和流形正则化的图像聚类算法(CRNMF),将相关熵、稀疏约束和流形正则集成为一个统一框架.采用相关熵代替传统NMF中的欧氏距离,在充分学习数据的局部结构的同时对非负矩阵进行稀疏约束,有效抑制非高斯噪声和异常值的影响.最后,采用半二次优化技术(HQ)导出CRNMF的乘法更新规则,证明了算法的正确性和收敛性.在五个图像数据集上进行实验,并与经典的聚类算法进行比较,证明CRNMF的聚类精度(ACC )、归一化互信息(NMI )和纯度(PUR )都有所提高.
尽管CRNMF在聚类任务中取得了较好的效果,但仅限于处理非高斯噪声.为了处理更加复杂的噪声,未来的工作将进一步提高CRNMF的有效性和鲁棒性.首先,拓展所提出的算法,增加双图调节或超图约束;其次,充分利用数据中的监督信息,研究算法在半监督学习中的性能;最后,将所提出的算法应用到多视图聚类任务中.
参考文献
View Option
[1]
Hartigan J A Wong M A Algorithm AS 136:A k ⁃means clustering algorithm
Applied Statistics ,1979 ,28 (1 ):100 -108 .
[本文引用: 1]
[2]
Von Luxburg U A tutorial on spectral clustering
Statistics and Computing ,2007 ,17 (4 ):395 -416 .
[本文引用: 1]
[3]
Lee D D Seung H S Algorithms for non⁃negative matrix factorization
∥Proceedings of the 13th International Conference on Neural Information Processing Systems . Cambridge,MA,USA :MIT Press ,2000 (13 ):535 -541 .
[本文引用: 2]
[4]
Jain A K Data clustering:50 years beyond k ⁃means
Pattern Recognition Letters ,2010 ,31 (8 ):651 -666 .
[本文引用: 1]
[5]
Kriegel H P Kröger P Zimek A Clustering high⁃dimensional data:A survey on subspace clustering,pattern⁃based clustering,and correlation clustering
ACM Transactions on Knowledge Discovery from Data ,2009 ,3 (1 ):1 .
[6]
Chakraborty S Paul D Das S et al Entropy regularized power k ⁃means clustering
2020 ,arXiv ,2001 .03452 .
[本文引用: 1]
[7]
Wang Y X Zhang Y J Nonnegative matrix factorization:A comprehensive review
IEEE Transactions on Knowledge and Data Engineering ,2013 ,25 (6 ):1336 -1353 .
[本文引用: 1]
[8]
Tolić D Antulov⁃Fantulin N Kopriva I A nonlinear orthogonal non⁃negative matrix factorization approach to subspace clustering
Pattern Recognition ,2018 (82 ):40 -55 .
[本文引用: 1]
[9]
Liu G C Lin Z C Yan S C et al Robust recovery of subspace structures by low⁃rank representation
IEEE Transactions on Pattern Analysis and Machine Intelligence ,2013 ,35 (1 ):171 -184 .
[本文引用: 1]
[10]
Jolliffe I T Principal component analysis
Journal of Marketing Research ,2002 ,87 (4 ):513 .
[本文引用: 1]
[11]
Höcker A Kartvelishvili V SVD approach to data unfolding
Nuclear Instruments and Methods in Physics Research Section A:Accelerators,Spectrometers,Detectors and Associated Equipment ,1996 ,372 (3 ):469 -481 .
[本文引用: 1]
[12]
Lee D D Seung H S Learning the parts of objects by non⁃negative matrix factorization
Nature ,1999 ,401 (6755 ):788 -791 .
[本文引用: 2]
[13]
Li S Z Hou X W Zhang H J et al Learning spatially localized,parts⁃based representation
∥Proceedings of 2001 IEEE Computer Society Conference on Computer Vision and Pattern Recognition . Kauai,HI,USA :IEEE ,2001 :5 .
[本文引用: 1]
[14]
Ullman S High⁃level vision:Object⁃recognition and visual cognition
Optical Engineering ,1997 ,36 (11 ):231 -256 .
[本文引用: 1]
[15]
Logothetis N K Sheinberg D L Visual object recognition
Annual Review of Neuroscience ,1996 (19 ):577 -621 .
[本文引用: 1]
[16]
Liu X W Wang L Zhang J et al Global and local structure preservation for feature selection
IEEE Transactions on Neural Networks and Learning Systems ,2017 ,25 (6 ):1083 -1095 .
[本文引用: 1]
[17]
Chen J Ma Z M Liu Y Local coordinates alignment with global preservation for dimensionality reduction
IEEE Transactions on Neural Networks and Learning Systems ,2013 ,24 (1 ):106 -117 .
[18]
Luong K Nayak R Learning inter⁃ and intra⁃manifolds for matrix factorization⁃based multi⁃aspect data clustering
IEEE Transactions on Knowledge and Data Engineering ,2020 ,DOI:10.1109/TKDE. 2020.3022072 .
[本文引用: 1]
[19]
Cai D He X F Han J W et al Graph regularized nonnegative matrix factorization for data representation
IEEE Transactions on Pattern Analysis and Machine Intelligence ,2011 ,33 (8 ):1548 -1560 .
[本文引用: 3]
[20]
He P Xu X H Ding J et al Low⁃rank nonnegative matrix factorization on stiefel manifold
Information Sciences ,2020 (514 ):131 -148 .
[本文引用: 1]
[21]
Guan N Y Tao D C Luo Z G et al Manifold regularized discriminative nonnegative matrix factorization with fast gradient descent
IEEE Transactions on Image Processing ,2011 ,20 (7 ):2030 -2048 .
[本文引用: 1]
[22]
Shang F H Jiao L C Wang F Graph dual regularization non⁃negative matrix factorization for co⁃clustering
Pattern Recognition ,2012 ,45 (6 ):2237 -2250 .
[本文引用: 1]
[23]
Zeng K Yu J Li C H et al Image clustering by hyper⁃graph regularized non⁃negative matrix factorization
Neurocomputing ,2014 (138 ):209 -217 .
[本文引用: 1]
[24]
Li H R Zhang J S Shi G et al Graph⁃based discriminative nonnegative matrix factorization with label information
Neurocomputing ,2017 (266 ):91 -100 .
[本文引用: 2]
[25]
Wang Y Y Wu S Y Mao B et al Correntropy induced metric based graph regularized non⁃negative matrix factorization
Neurocomputing ,2016 (204 ):172 -182 .
[本文引用: 2]
[26]
Du L Xuan L Shen Y D Robust nonnegative matrix factorization via half⁃quadratic minimization
∥2012 IEEE 12th International Conference on Data Mining . Brussels,Belgium :IEEE ,2013 :201 -210 .
[本文引用: 1]
[27]
Li L Yang J J Zhao K L et al Graph regularized
[本文引用: 1]
non⁃negative matrix factorization by maximizing correntropy Journal of Computers ,2014 ,9 (11 ):2570 -2579 .
[本文引用: 1]
[28]
Zhou N Xu Y Y Cheng H et al Maximum correntropy criterion⁃based sparse subspace learning for unsupervised feature selection
IEEE Transactions on Circuits and Systems for Video Technology ,2019 ,29 (2 ):404 -417 .
[本文引用: 2]
[29]
谢林江 ,尹东 基于最大相关熵准则的鲁棒度量学习算法
计算机系统应用 ,2018 ,27 (10 ):146 -153 .
[本文引用: 1]
Xie L J Yin D Robust metric learning based on maximum correntropy criterion
Computer Systems and Applications ,2018 ,27 (10 ):146 -153 .
[本文引用: 1]
[30]
Yu N Wu M J Liu J X et al Correntropy⁃based hypergraph regularized NMF for clustering and feature selection on multi⁃cancer integrated data
IEEE Transactions on Cybernetics ,2020 ,51 (8 ):3952 -3963 .
[本文引用: 2]
[31]
Peng S Y Ser W Lin Z P et al Robust sparse nonnegative matrix factorization based on maximum correntropy criterion
∥2018 IEEE International Symposium on Circuits and Systems . Florence,Italy :IEEE ,2018 :1 -5 .
[本文引用: 3]
[32]
Zhang L F Zhang Q Du B et al Robust manifold matrix factorization for joint clustering and feature extraction
∥31st AAAI Conference on Artificial Intelligence . San Francisco,CA,USA :Machine Learning Applications ,2017 :1662 -1668 .
[本文引用: 1]
[33]
Chen G F Xu C Wang J Y et al Robust non⁃negative matrix factorization for link prediction in complex networks using manifold regularization and sparse learning
Physica A:Statistical Mechanics and its Applications ,2020 ,539 :122882 ,DOI:10.1016/j.physa.2019.122882 .
[本文引用: 2]
[34]
Belkin M Niyogi P Sindhwani V Manifold regularization:A geometric framework for learning from Labeled and Unlabeled examples
The Journal of Machine Learning Research ,2006 ,7 (1 ):2399 -2434 .
[本文引用: 1]
[35]
Peng S Y Chen B D Sun L et al Constrained maximum correntropy adaptive filtering
Signal Processing ,2017 ,140 :116 -126 .
[本文引用: 1]
[36]
Peng S Y Ser W Chen B D et al Robust semi⁃supervised nonnegative matrix factorization for image clustering
Pattern Recognition ,2021 (111 ):107683 ,DOI:10.1016/j.patcog.2020.107683 .
[本文引用: 2]
[37]
He R Hu B G Yuan X T et al Robust recognition via information theoretic learning . New York :Springer ,2014 .
[本文引用: 1]
[38]
Lovász L Plummer M D Matching theory . Amsterdam,The Netherlands :North⁃Holland ,1986 :544 .
[本文引用: 1]
Algorithm AS 136:A k ?means clustering algorithm
1
1979
... 聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用. ...
A tutorial on spectral clustering
1
2007
... 聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用. ...
Algorithms for non?negative matrix factorization
2
2000
... 聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用. ...
... 假设X = x 1 , x 2 , … , x N ∈ ℝ ≥ 0 M × N X M [3 ] 可以表示为: ...
Data clustering:50 years beyond k ?means
1
2010
... 聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用. ...
Clustering high?dimensional data:A survey on subspace clustering,pattern?based clustering,and correlation clustering
0
2009
Entropy regularized power k ?means clustering
1
2020
... 聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用. ...
Nonnegative matrix factorization:A comprehensive review
1
2013
... 聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用. ...
A nonlinear orthogonal non?negative matrix factorization approach to subspace clustering
1
2018
... 聚类的目的是将相似度高的数据点聚为一类,将相似度低的数据点聚为不同类.由于聚类在机器学习、数据挖掘、计算机视觉等领域受到广泛关注,如何降低噪声和异常值对聚类结果的影响已成为一个重要课题.几十年来,大量的聚类算法被提出,例如k⁃ means[1 ] 、谱聚类(Spectral Clustering,SC)[2 ] 和非负矩阵分解(Non⁃Negative Matrix Factorization,NMF)[3 ] 等.k⁃ means既是基于划分的聚类算法,也是基于矩阵分解的聚类算法,虽然实现速度快,但无法处理非线性数据.谱聚类可以用来处理非线性数据,但其计算成本较高.大多数情况下,现实世界聚类任务中遇到的数据维数非常高,传统的聚类算法及其变种[4 -6 ] 因为噪声和冗余的影响,处理高维数据的性能不佳,因此,发现高维数据的低维表示尤为重要.由于NMF对数据表示良好的可解释性和明确的物理意义,已成为最流行的维度还原算法之一[7 -8 ] .本文主要研究NMF在聚类中的应用. ...
Robust recovery of subspace structures by low?rank representation
1
2013
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Principal component analysis
1
2002
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
SVD approach to data unfolding
1
1996
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Learning the parts of objects by non?negative matrix factorization
2
1999
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
... [12 ]之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Learning spatially localized,parts?based representation
1
2001
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
High?level vision:Object?recognition and visual cognition
1
1997
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Visual object recognition
1
1996
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Global and local structure preservation for feature selection
1
2017
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Local coordinates alignment with global preservation for dimensionality reduction
0
2013
Learning inter? and intra?manifolds for matrix factorization?based multi?aspect data clustering
1
2020
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Graph regularized nonnegative matrix factorization for data representation
3
2011
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
... 与其他矩阵分解算法最大的不同是,NMF对U V [19 ] . ...
... 为了证明提出的CRNMF算法在聚类任务中的有效性和鲁棒性,将CRNMF与七种相关聚类算法进行比较,它们是k⁃ means,NMF,GNMF[19 ] ,CGNMF[25 ] ,GDNMF[24 ] ,GLoRSS[28 和l 1 ⁃CNMF[31 ] .在这些比较算法中,k⁃ means是基线. ...
Low?rank nonnegative matrix factorization on stiefel manifold
1
2020
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Manifold regularized discriminative nonnegative matrix factorization with fast gradient descent
1
2011
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Graph dual regularization non?negative matrix factorization for co?clustering
1
2012
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Image clustering by hyper?graph regularized non?negative matrix factorization
1
2014
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
Graph?based discriminative nonnegative matrix factorization with label information
2
2017
... 传统矩阵分解有低秩表示(Latent Low⁃Rank Representation,LRR)[9 ] 、主成分分析(Principal Components Analysis,PCA)[10 ] 和奇异值分解(Singular Value Decomposition,SVD)[11 ] 等.与它们不同,NMF的目标是学习两个低维非负矩阵,即分解后的两个非负矩阵的乘积能够逼近原始数据矩阵.由于施加在低维子空间中分解矩阵上的非负约束条件且只允许学习矩阵的加法组合,NMF只学习基于部分的数据表示[12 -13 ] .更重要的是,NMF符合大脑中人类认知过程的直观概念,即结合部分形成整体,这已在心理学和生理学中得到研究[14 -15 ] .因此,NMF可以被认为是一种优秀的降维算法,并已成功应用于包括文本分析和图像处理在内的各种实际应用中.一般地,大多数传统NMF及其扩展算法中的矩阵分解的目标函数或优化准则是基于欧式距离或KL (Kullback⁃Leibler)散度,因为它们具有简单、良好的数学性质和对高斯噪声不敏感等优点.然而在许多实际应用中,数据通常包含不同类型的非高斯噪声和异常值,这种情况下,传统NMF算法及其扩展的性能很差.在Lee and Seung[12 ] 之后,受到上述原始NMF优越特性的激励,NMF受欢迎的程度日益提高.随后,为了解决不同的问题,提出了许多以NMF为代表的变体和扩展.但是,如果不考虑数据的流形结构,传统NMF算法的性能依旧很差.因此,保持数据流形结构的重要性在机器学习、数据挖掘和模式识别的研究领域引起了相当大的关注[16 -18 ] .例如,图正则化非负矩阵分解(Graph Regularized Non⁃Negative Matrix Factorization,GNMF)充分利用数据的固有几何结构,通过拉普拉斯正则化将数据空间建模为嵌入在环境空间中的流形.GNMF同时考虑了原始空间中数据点的线性和非线性关系,与只考虑欧氏距离的普通NMF区别很大[19 -20 ] ,因此GNMF比普通NMF更适合聚类问题.在此基础上,Guan et al[21 ] 充分考虑数据的几何结构和不同类别的判别信息,提出流形正则化判别非负矩阵分解算法(Manifold Regularized Discriminative Non⁃Negative Matrix Factorization,MD⁃NMF).Shang et al[22 ] 提出一种考虑样本流形和特征流形的图对偶正则化算法(Graph Dual Regularization Non⁃Negative Matrix Factorization,DNMF),用于处理共聚类问题.Zeng et al[23 ] 提出超图正则化算法(Hyper⁃Graph Regularized Non⁃Negative Matrix Factorization,HNMF)来更好地反映数据中固有的几何结构.Li et al[24 ] 同时考虑标签信息和局部流形正则化,提出基于图的判别非负矩阵分解算法 (Graph⁃Based Discriminative Non⁃Negative Matrix Factorization,GDNMF),通过构造p⁃ 近邻图对数据的局部几何结构进行编码,并在NMF中考虑标签信息,增强了聚类表示的区分能力. ...
... 为了证明提出的CRNMF算法在聚类任务中的有效性和鲁棒性,将CRNMF与七种相关聚类算法进行比较,它们是k⁃ means,NMF,GNMF[19 ] ,CGNMF[25 ] ,GDNMF[24 ] ,GLoRSS[28 和l 1 ⁃CNMF[31 ] .在这些比较算法中,k⁃ means是基线. ...
Correntropy induced metric based graph regularized non?negative matrix factorization
2
2016
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
... 为了证明提出的CRNMF算法在聚类任务中的有效性和鲁棒性,将CRNMF与七种相关聚类算法进行比较,它们是k⁃ means,NMF,GNMF[19 ] ,CGNMF[25 ] ,GDNMF[24 ] ,GLoRSS[28 和l 1 ⁃CNMF[31 ] .在这些比较算法中,k⁃ means是基线. ...
Robust nonnegative matrix factorization via half?quadratic minimization
1
2013
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
Graph regularized
1
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
1
2014
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
Maximum correntropy criterion?based sparse subspace learning for unsupervised feature selection
2
2019
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
... 由于对非高斯噪声和异常值的鲁棒性,相关熵已被广泛应用.作为一个非线性和局部相似性度量函数,相关熵直接与相似随机变量A 和B 在联合空间邻域中的概率有关,定义如下[28 ,35 -36 ] : ...
基于最大相关熵准则的鲁棒度量学习算法
1
2018
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
Robust metric learning based on maximum correntropy criterion
1
2018
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
Correntropy?based hypergraph regularized NMF for clustering and feature selection on multi?cancer integrated data
2
2020
... 以上算法都使用欧式距离来最小化原始数据矩阵和重构矩阵之间的距离,由于欧式距离的可解释性和可处理性,已被广泛应用于基于NMF的算法中.然而,基于欧式距离的NMF对非高斯噪声和异常值敏感,进行聚类任务时性能显著降低,因此,相关熵被提出用于处理基于NMF的任务.Wang et al[25 ] 将相关熵引入GNMF,提出一种用于图像聚类的非负矩阵分解算法(Correntropy Induced Metric Based Graph Regularized Non⁃Negative Matrix Factorization,CGNMF),在考虑数据流形结构的同时增强算法的鲁棒性.Du et al[26 ] 提出一种基于相关熵诱导度量的鲁棒算法(Robust Non⁃Negative Matrix Factorization Method Based on the Correntropy Induced Metric,CIM⁃NMF),通过结合关于离群点的结构知识导出用于处理离群点的基于行的CIM⁃NMF.Li et al[27 ] 通过最大化用于非可视化图像聚类的相关熵准则,发展图正则化的非负矩阵分解算法(Graph Regularized Non⁃Negative Matrix Factorization by Maximizing Correntropy,GRNMF).Zhou et al[28 ] 提出一种无监督的特征选择算法,称为基于相关熵的全局和局部保持鲁棒稀疏子空间学习算法(Global and Local Structure Preserving Robust Sparse Subspace Learning,GLoRSS).谢林江和尹东[29 ] 提出基于最大相关熵准则的鲁棒度量学习算法,将相关熵引入度量学习来更好地实现分类.Yu et al[30 ] 提出用于癌症聚类的超图正则化非负矩阵分解算法(Correntropy⁃Based Hypergraph Regularized Non⁃Negative Matrix Factorization,CHNMF),用相关熵代替欧氏距离来提高鲁棒性并引入超图正则化项,在癌症数据集上效果较好. ...
... 通常,基于信息论学习(Information Theoretic Learning,ITL)方法的目标函数是非线性的且非凸的,难以直接进行优化.幸运的是,HQ常被用来解决基于ITL的优化问题[30 -31 ,36 ] .假设ϕ e e ∈ ℝ M
Robust sparse nonnegative matrix factorization based on maximum correntropy criterion
3
2018
... 同时,引入范数对矩阵进行稀疏约束来发展一些稳健的NMF算法.Peng et al[31 ] 提出一种基于相关熵的鲁棒非负矩阵分解算法(l 1 ⁃Norm Non⁃Negative Matrix Factorization Based on Maximum Correntropy Criterion,l 1 ⁃CNMF),将传统的NMF算法与l 1 ⁃范数和最大相关熵准则结合,对系数矩阵进行稀疏约束,在图像聚类任务中取得了较好的效果.Zhang et al[32 ] 提出基于l 2,1 ⁃范数的矩阵分解来获得抗噪声和离群点的鲁棒解.Chen et al[33 ] 提出基于流形正则化和稀疏学习的鲁棒非负矩阵分解算法(Robust Non⁃Negative Matrix Factorization via Jointly Manifold Regularization and Sparse Learning,MS⁃RNMF),在NMF中引入l 2,1 ⁃范数约束,同时对基矩阵和系数矩阵进行稀疏约束. ...
... 通常,基于信息论学习(Information Theoretic Learning,ITL)方法的目标函数是非线性的且非凸的,难以直接进行优化.幸运的是,HQ常被用来解决基于ITL的优化问题[30 -31 ,36 ] .假设ϕ e e ∈ ℝ M
... 为了证明提出的CRNMF算法在聚类任务中的有效性和鲁棒性,将CRNMF与七种相关聚类算法进行比较,它们是k⁃ means,NMF,GNMF[19 ] ,CGNMF[25 ] ,GDNMF[24 ] ,GLoRSS[28 和l 1 ⁃CNMF[31 ] .在这些比较算法中,k⁃ means是基线. ...
Robust manifold matrix factorization for joint clustering and feature extraction
1
2017
... 同时,引入范数对矩阵进行稀疏约束来发展一些稳健的NMF算法.Peng et al[31 ] 提出一种基于相关熵的鲁棒非负矩阵分解算法(l 1 ⁃Norm Non⁃Negative Matrix Factorization Based on Maximum Correntropy Criterion,l 1 ⁃CNMF),将传统的NMF算法与l 1 ⁃范数和最大相关熵准则结合,对系数矩阵进行稀疏约束,在图像聚类任务中取得了较好的效果.Zhang et al[32 ] 提出基于l 2,1 ⁃范数的矩阵分解来获得抗噪声和离群点的鲁棒解.Chen et al[33 ] 提出基于流形正则化和稀疏学习的鲁棒非负矩阵分解算法(Robust Non⁃Negative Matrix Factorization via Jointly Manifold Regularization and Sparse Learning,MS⁃RNMF),在NMF中引入l 2,1 ⁃范数约束,同时对基矩阵和系数矩阵进行稀疏约束. ...
Robust non?negative matrix factorization for link prediction in complex networks using manifold regularization and sparse learning
2
2020
... 同时,引入范数对矩阵进行稀疏约束来发展一些稳健的NMF算法.Peng et al[31 ] 提出一种基于相关熵的鲁棒非负矩阵分解算法(l 1 ⁃Norm Non⁃Negative Matrix Factorization Based on Maximum Correntropy Criterion,l 1 ⁃CNMF),将传统的NMF算法与l 1 ⁃范数和最大相关熵准则结合,对系数矩阵进行稀疏约束,在图像聚类任务中取得了较好的效果.Zhang et al[32 ] 提出基于l 2,1 ⁃范数的矩阵分解来获得抗噪声和离群点的鲁棒解.Chen et al[33 ] 提出基于流形正则化和稀疏学习的鲁棒非负矩阵分解算法(Robust Non⁃Negative Matrix Factorization via Jointly Manifold Regularization and Sparse Learning,MS⁃RNMF),在NMF中引入l 2,1 ⁃范数约束,同时对基矩阵和系数矩阵进行稀疏约束. ...
... 为了保留局部信息,结合流形正则化和局部相似度使数据点达到无差异[33 ] .vi 和vj 是与数据点xi ,xj 关联的特征向量.通过1 2 m i n ∑ i , j v i - v j 2 vi 和vj 之间的微小差异.因此,局部相似度得分越高则数据点之间的差异越小,定义如下: ...
Manifold regularization:A geometric framework for learning from Labeled and Unlabeled examples
1
2006
... 在许多现实世界的应用中,数据点常位于一个低维的流形上,因此流形学习引起了巨大的关注.通常,邻近的数据点可能有相似的特征并被分类或划分到同一组中.假设邻近的数据点在新的数据空间中也是相近的,称为“流形假设”[34 ] .将“流形假设”引入非负矩阵分解中,即局部流形学习,以期望小邻域内的邻近数据点可以共享内在的几何结构. ...
Constrained maximum correntropy adaptive filtering
1
2017
... 由于对非高斯噪声和异常值的鲁棒性,相关熵已被广泛应用.作为一个非线性和局部相似性度量函数,相关熵直接与相似随机变量A 和B 在联合空间邻域中的概率有关,定义如下[28 ,35 -36 ] : ...
Robust semi?supervised nonnegative matrix factorization for image clustering
2
... 由于对非高斯噪声和异常值的鲁棒性,相关熵已被广泛应用.作为一个非线性和局部相似性度量函数,相关熵直接与相似随机变量A 和B 在联合空间邻域中的概率有关,定义如下[28 ,35 -36 ] : ...
... 通常,基于信息论学习(Information Theoretic Learning,ITL)方法的目标函数是非线性的且非凸的,难以直接进行优化.幸运的是,HQ常被用来解决基于ITL的优化问题[30 -31 ,36 ] .假设ϕ e e ∈ ℝ M
1
2014
... 显然,上述目标函数(16)的优化问题很难直接解决,因为目标函数(16)中的U V [37 ] ,因此,本文使用基于共轭函数理论的HQ对CRNMF进行优化.首先将非凸目标函数转化为乘法形式的二次函数,然后利用乘法更新规则对转化后的二次函数进行求解.基于凸共轭函数的性质,有以下命题: ...
1
1986
... h = z δ m a p ⋅ [38 ] 将每个聚类标签映射到来自数据集的等价标签的映射函数. ...