时态图是一种多重边动态图,在时态图中任意两个顶点之间可以存在多条边,并且每条边包含额外的时间信息.时态图中的顶点和边会随时间不断发生变化,新的顶点(边)会被插入或删除,因此时态图在多个时间点拥有不同的快照.现实中很多系统都可以被抽象为时态图,如线上社交网络、航空运输网络、蛋白质相互作用网络等,如何在这些复杂网络中挖掘有价值的信息或区域一直是研究人员密切关心的问题.
本文提出一种面向大规模时态图的
1 相关工作
在简单图中,对图中所有的
在一种特殊的动态图——时态图中,任意两个顶点之间可以同时存在多条边,因此时态图的紧密子图
2 背景知识
表1为本文使用的数学符号及其含义.
表1 文中使用的数学符号表
Table 1
| 符号 | 描述 |
|---|---|
| 时态图 | |
| 一张时态图 | |
| 上一时刻的时态图 | |
| 当前时刻的时态图 | |
| 部分 | |
| 插入子图 | |
| 删除子图 | |
| 时态图 | |
| 时态图 | |
| 时态图中任意一个顶点 | |
| 时态图中任意一个顶点 | |
| 时态图中任意一条边 | |
| 图 | |
| 图 | |
| 图 | |
| 图 | |
| 图 | |
| 图 |
2.1 时态图
时态图是一种特殊的无环无向无权多重图,其中每条边都带有额外的时间信息,用于指明这条边的生存周期,即边从第一次出现到消失的时间段.对于时态图
为了方便表述,本文简化了一些符号.对于时态图
为了更好地描述两张时态图之间的联系,还定义了一些在时态图上的集合操作.对于给定的两张时态图
2.2
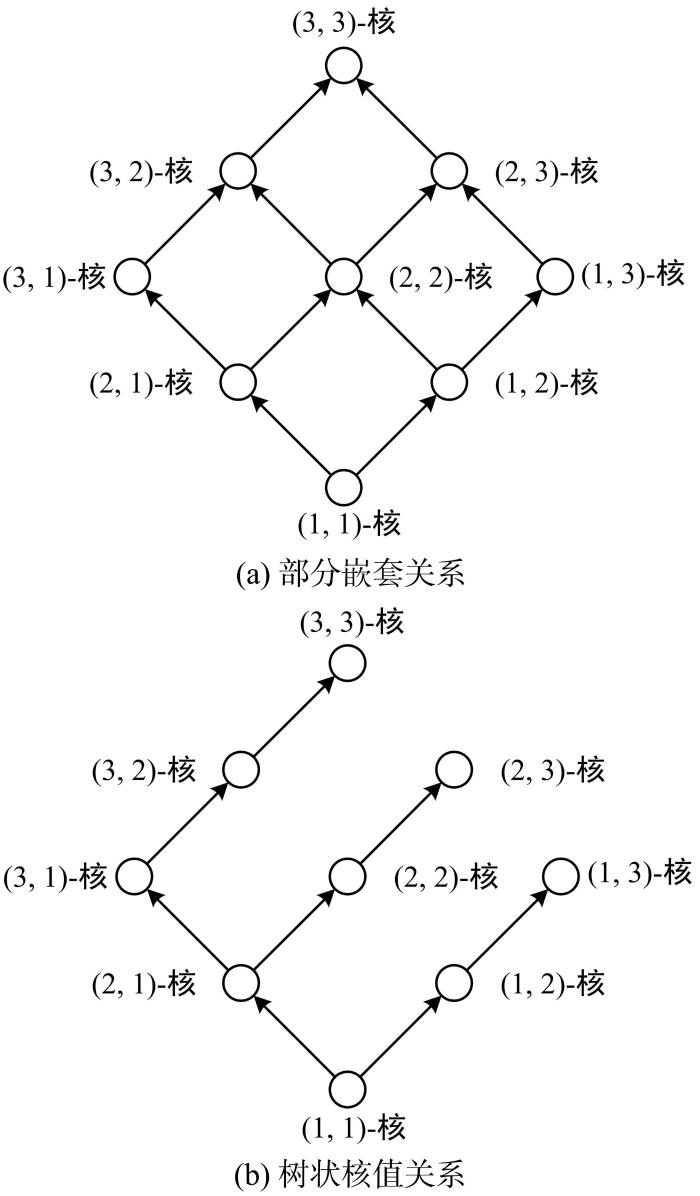
与k⁃核不同的是,
对于任意一条边,有:
图1
扩展图 给定两张时态图
满足
且
则
扩展图具有以下特征:如果
类似
图:令
对于任意一条边
值得注意的是,类似
部分
当前时刻有新的边插入时态图时,为了估计新插入的边对时态图中顶点核值的影响范围,还需要引入候选插入子图的概念.候选插入子图的定义及其解释详见下文.
此外,给定一张时态图
3 自顶向下的时态图
本文提出一种由紧密到稀疏、自顶向下的时态图
对于
当算法只维护最紧密的
对一个受到插入边影响而需要更新的
候选插入子图 令:
如果图
自顶向下的时态图
根据
根据定义5可以发现,
算法1介绍了识别候选插入子图的具体方法.由于该算法只涉及图的遍历操作,因此时间复杂度不会超过
候选插入子图识别算法
输入:当前时刻的时态图快照
输出:候选插入子图
1.定义一个空的顶点集合
2.将所有
3.while
4. 从
5. for all 顶点
6. if
7. if
8. 将
9. if
10. 将顶点
11.输出此时的
在获得候选插入子图后,还需考虑如何利用候选插入子图识别部分
令:
那么:
定理1的证明略.
如果
令:
根据定义3,可知
综上,
令:
那么:
令:
首先证明
接下来证明
假设(a):存在一张非空时态图
假设(b):
对于任意一条边
综上,得出
综上,
令:
那么:
定理3的证明略.
那么:
令
首先根据定义5,当:
时
综上,
综上,
基于以上四个定理,本文提出一种部分
部分
输入:候选插入子图
核
输出:部分
1.if
2. 初始化顶点队列
3. for all
4. if
5. 将
6. while
7. 从
8. for all
9. if
10. 将
11. 将
12. 此时的
13.else
14. 利用
15.输出部分
最后,提出一种自顶向下的时态图
自顶向下的时态图
输入:当前时刻的时态图快照
输出:当前时刻最紧密的
1.计算所有类似
2.初始化不重复队列
3.计算
4.将
5.while
6. 从
7. if
8.
9. if
10. 令
11. 根据算法1计算
12. 根据算法2计算
13. if
14. 将
15. 若
16. if
17. 将
18.输出当前时刻最紧密的
算法3第1行利用QTCDNG算法[16]计算
图2展示了自顶向下的时态图
图2
图2
当插入
Fig.2
The process of top⁃down maintenance of the temporal graph
4 自顶向下的时态图
当有上一时刻时态图中存在的边在当前时刻被删除时,删除子图
算法4展示了对于单独一个
单一
输入:类似
输出:当前时刻的
1.定义一个空的用于存储顶点的队列
2.for all
3. 将
4. if
5. 将
6. if
7. 将顶点
8. if
9. 将顶点
10.while
11. 从
12. for all
13. 删除
14. if
15. 将顶点
16. 将顶点
17.输出当前的
在算法4的基础上,自顶向下的时态图
自顶向下的时态图
输入:当前时刻的时态图快照
输出:当前时刻最紧密的
1.计算所有的类似
2.定义一个空的用于存储
3.将所处层数与上一时刻时态核层数的最大值相同的所有
4.初始化
5.while
6. 从
7. if
8. 用
9. if
10. 利用算法4计算
11. if
12. 将
13. 若
14. if
15. 将
16.输出当前时刻最紧密的
需要注意,当只有自顶向下维护最紧密的前
接下来,算法5第10~12行利用算法4完成删边时对每一个
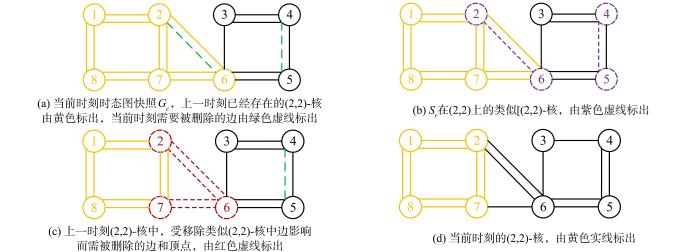
图3展示了自顶向下的时态图
图3
图3
当删除
Fig.3
The process of top⁃down maintenance of temporal graph
5 实验结果与分析
实验平台:CPU Xeon E5⁃2683v4 @ 2.1 GHz×2,内存128 GB,操作系统Linux.
使用的数据集均来自Network Repository和SNAP,选用10个真实存在的时态图数据集,分别为ia⁃contact (IC),ia⁃contacts⁃dublin (ICD),ia⁃digg⁃reply (IDR),ia⁃enron⁃employees (IEE),ia⁃escorts⁃dynamic (IED),ia⁃enron⁃email⁃all (IEEA),sx⁃askubuntu (SA),ia⁃stackexch⁃user⁃marks⁃post⁃und (ISUMPU),rec⁃amazon⁃ratings (RAR),rec⁃stackoverflow (RS).表2详细介绍了这些图数据集的关键数据,其中
表2 真实时态图
Table 2
| IC | 274 | 28244 | 101 | 168 | 39 | 168 |
| ICD | 10972 | 415912 | 64 | 345 | 18 | 345 |
| IDR | 30,360 | 86203 | 283 | 25 | 9 | 25 |
| IEE | 150 | 24705 | 74 | 1117 | 14 | 1117 |
| IED | 10106 | 50412 | 311 | 39 | 11 | 39 |
| IEEA | 86978 | 1134990 | 1726 | 1353 | 53 | 1353 |
| SA | 157222 | 726639 | 5401 | 215 | 48 | 215 |
| ISUMPU | 545196 | 1302234 | 6121 | 4 | 24 | 4 |
| RAR | 2146057 | 5776660 | 12204 | 28 | 29 | 28 |
| RS | 545196 | 1301923 | 6121 | 2 | 24 | 2 |
接下来将这些图按照图的规模分为两组:规模较小的一组(IC,ICD,IDR,IEE,IED)用于测试算法的性能;规模较大的一组(IEEA,ISUMPU,RAR,SA,RS)用于测试算法的可扩展性.观察表2可以发现,
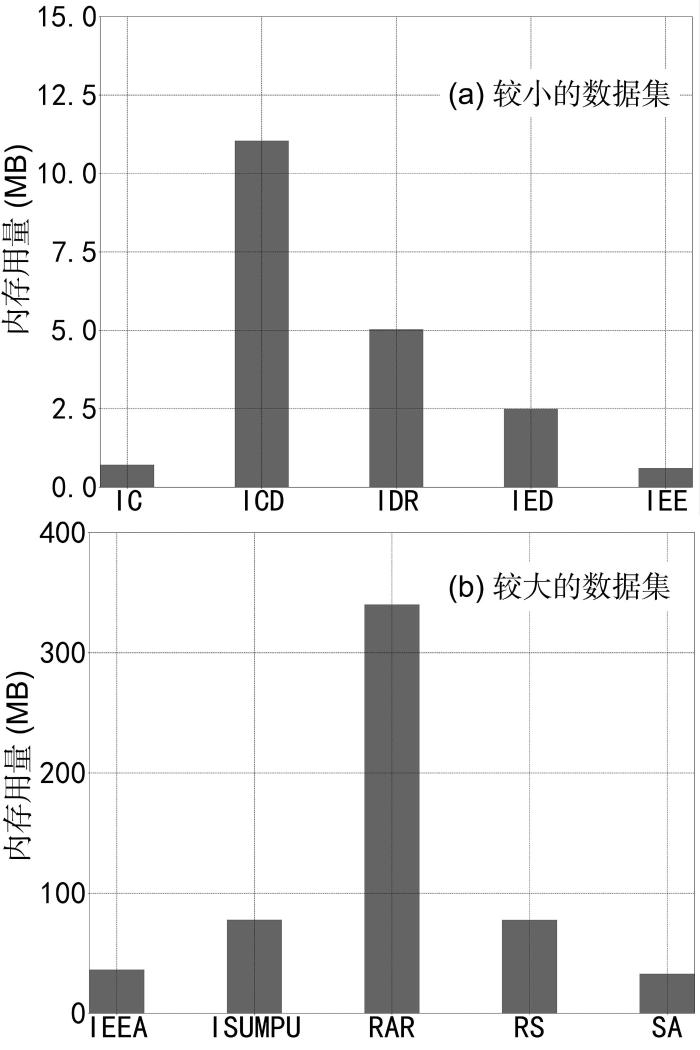
图4
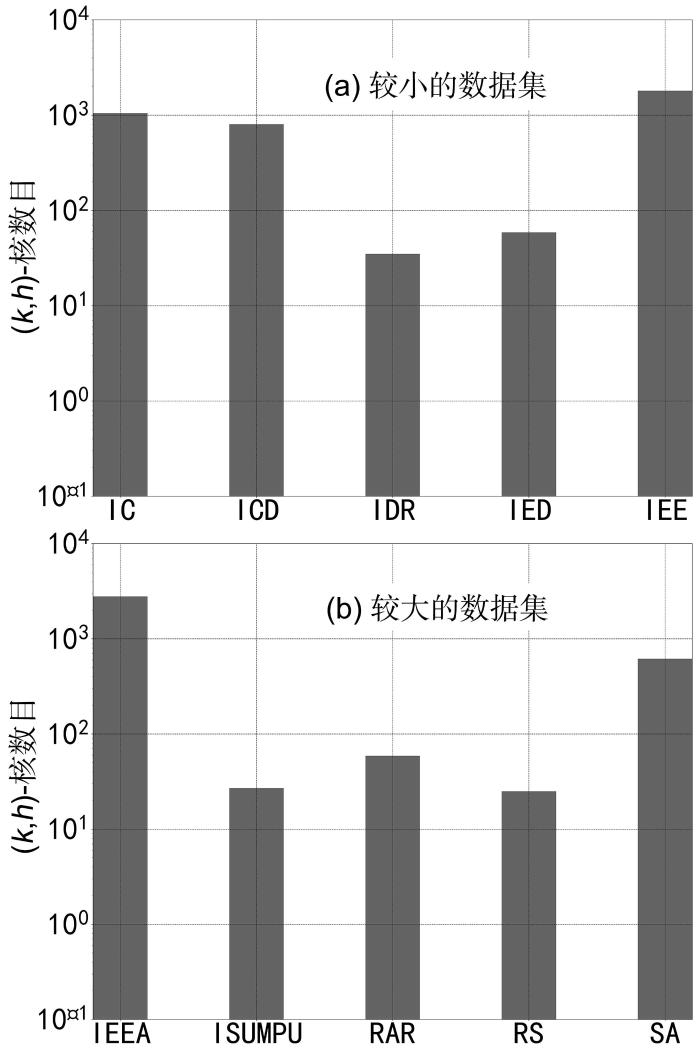
图5
为了体现时态图动态变化的过程,对于有新的边插入的情况,对实验所用时态图的所有边按照第一次出现的时间戳进行升序排序,使用排在最后的
5.1 对比算法与评价指标
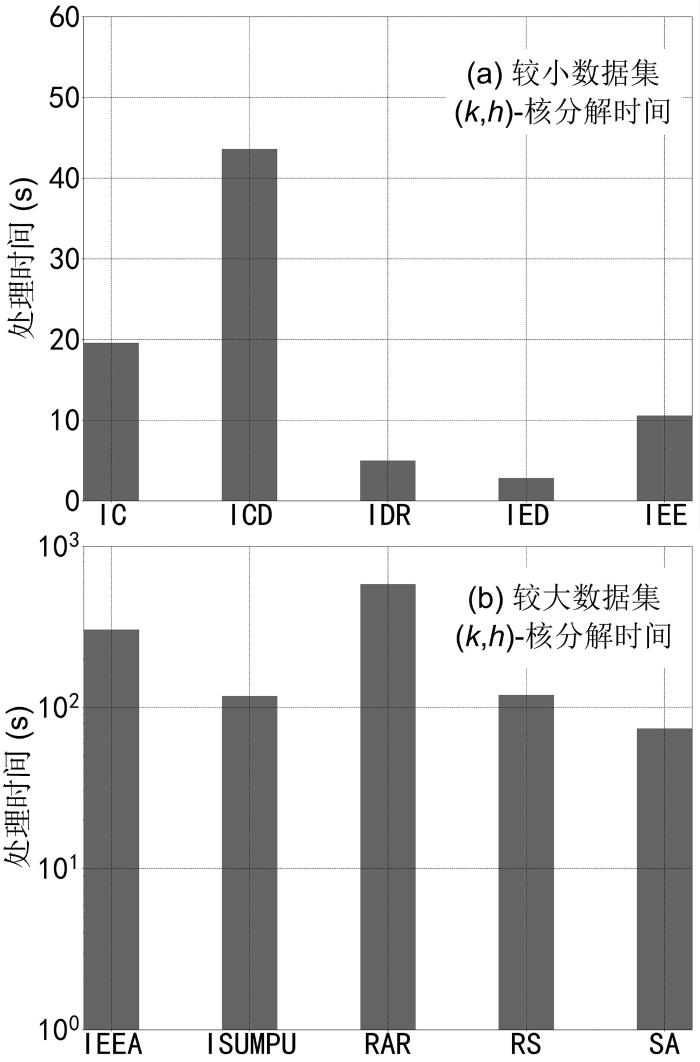
图6
图6
直接的
Fig.6
Processing time of direct
5.2 维护层数可扩展性
5.2.1 自顶向下的时态图
首先固定时态图中发生变化的边数为100条,研究需要维护的层数
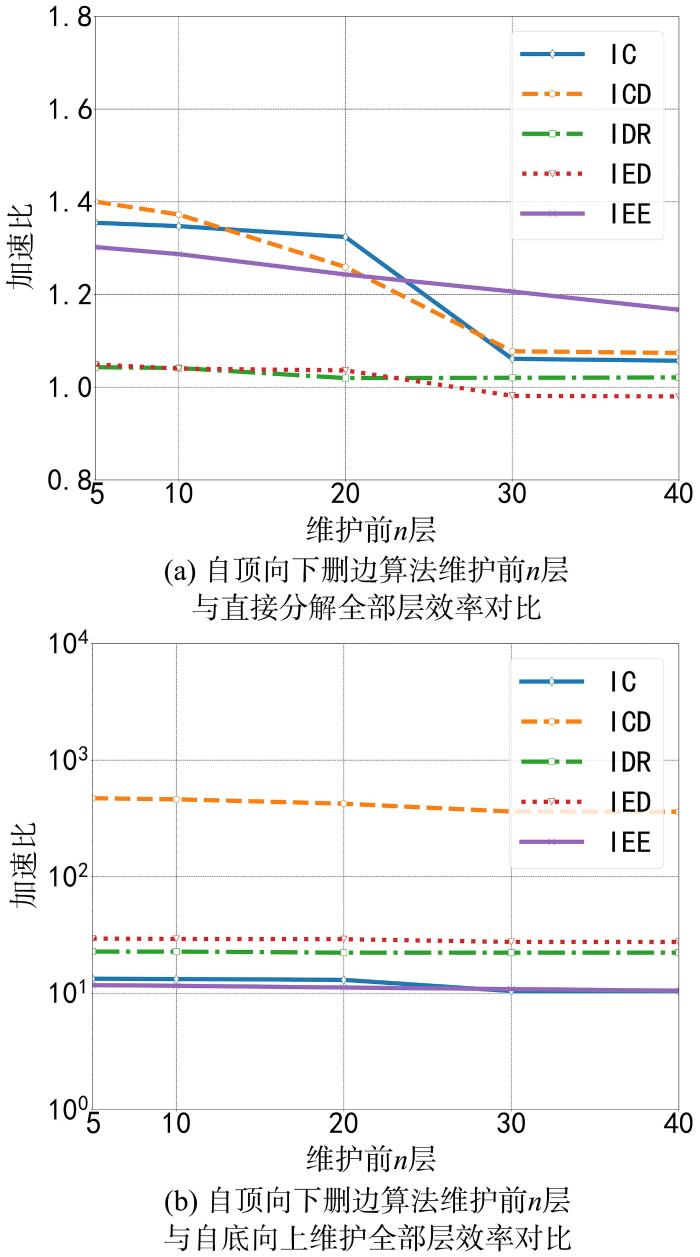
图7
图7
加边情况下维护全部层的效率
Fig.7
The algorithm efficiency of maintaining full layers when inserting edges
5.2.2 自顶向下的时态图
接下来,固定时态图中发生变化的边数为100,研究当需要维护的层数
图8
图8
删边情况下维护全部层的效率
Fig.8
The algorithm efficiency of maintaining full layers when removing edges
5.3 变化边数可扩展性
研究时态图中发生变化的边的数目对自顶向下的时态图
5.3.1 自顶向下的时态图
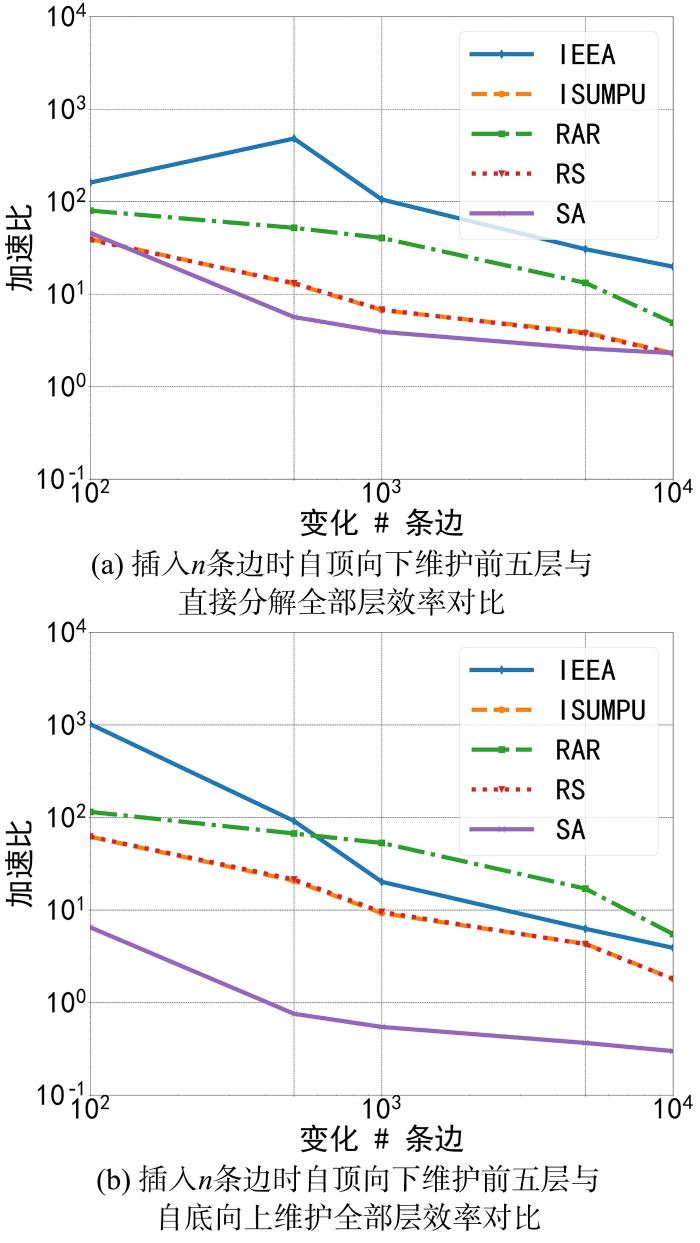
图9a展示了新插入边数不同时自顶向下维护前五层
图9
图9
加边情况下维护前五层的效率
Fig.9
The algorithm efficiency of maintaining the first five layers layers when inserting edges
图9b展示了插入边数不同时自顶向下维护前五层与自底向上维护全部层的效率对比.实验显示,加速比随着插入边数的增多整体呈降低趋势,但加速比始终大于1,意味着当插入边数不超过10000时,自顶向下维护前五层的效率始终比自底向上维护全部层高.此外,对比图9a和图9b,可以发现对于图IEEA和图SA,和直接重新进行
5.3.2 自顶向下的时态图
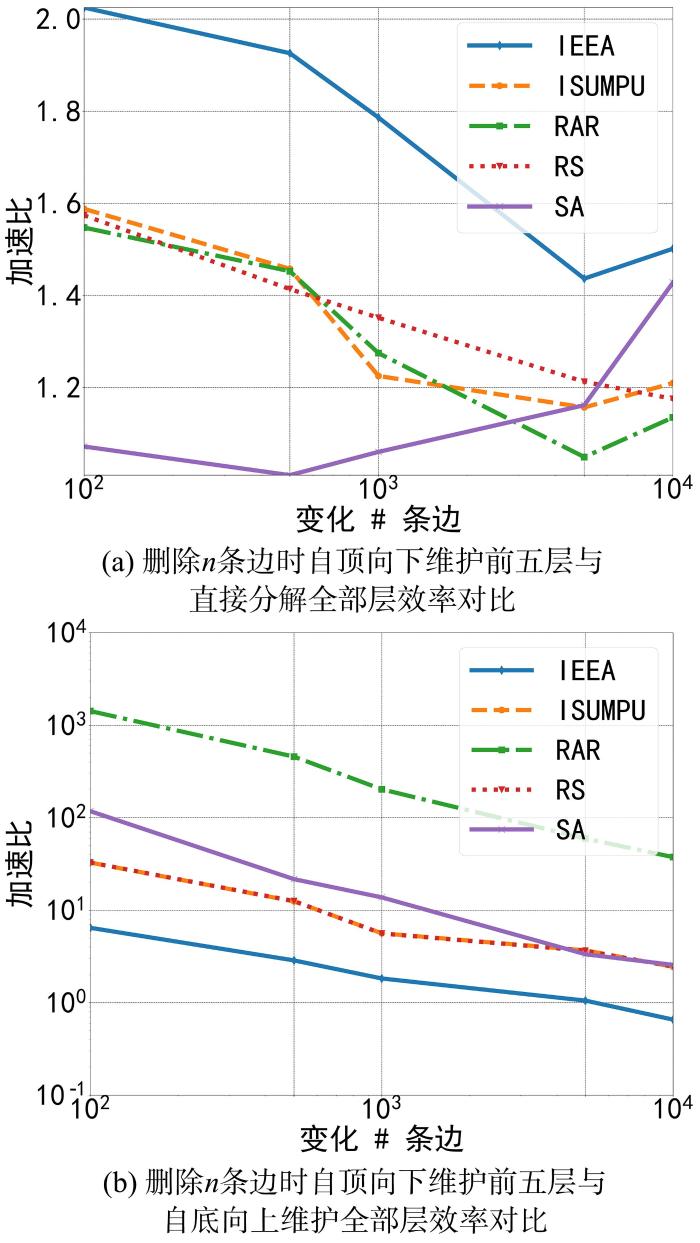
接下来讨论删除边数目对自顶向下的时态图
图10
图10
删边情况下维护前五层的效率
Fig.10
The algorithm efficiency of maintaining the first five layers layers when removing edges
图10b中,自顶向下的时态图
6 结论
本文对时态图中的紧密子图维护问题进行研究,提出一种自顶向下的时态图
参考文献
Core decomposition in large temporal graphs
∥
I/O efficient core graph decomposition:Application to degeneracy ordering
Querying k⁃truss community in large and dynamic graphs
∥
Finding the maximum clique in massive graphs
New heuristic approaches for maximum balanced biclique problem
Mining stable quasi⁃cliques on temporal networks
An ellipsoidal bounding scheme for the quasi⁃clique number of a graph
Adapted k⁃core decomposition and visualization for functional magnetic resonance imaging connectivity networks
∥
Accelerating community detection by using k⁃core subgraphs
Influential community search in large networks
基于k⁃核过滤的社交网络影响最大化算法
k⁃core filtered influence maximization algorithms in social networks
一种基于k⁃核的社会网络影响最大化算法
A k⁃core based algorithm for influence maximization in social networks
Using the k⁃core decomposition to analyze the static structure of large⁃scale software systems
Analyzing the structure of earthquake network by k⁃core decomposition
K⁃core based temporal graph convolutional network for dynamic graphs
Efficient temporal core maintenance of massive graphs
Clique relaxations in social network analysis:The maximum K⁃plex problem
An O(m) algorithm for cores decomposition of networks
Efficient core decomposition in massive networks
∥
I/O efficient Core Graph Decomposition at web scale
∥
Distributed k⁃core decomposition
Efficient core maintenance in large dynamic graphs
Streaming algorithms for k⁃core decomposition