锂电池二阶RC等效电路模型参数辨识

doi:10.13232/j.cnki.jnju.2020.05.015

锂电池二阶RC等效电路模型参数辨识

吴小慧, 张兴敢^,

南京大学电子科学与工程学院，南京，210023

Parameters identification of second order RC equivalent circuit model for lithium batteries

Wu Xiaohui, Zhang Xinggan^,

School of Electronic Science and Engineering, Nanjing University, Nanjing, 210023, China

通讯作者: E⁃mail：zhxg@nju.edu.cn

收稿日期: 2020-02-06 网络出版日期: 2020-09-27

Received: 2020-02-06 Online: 2020-09-27

摘要

以锂电池二阶RC等效电路模型为研究对象，将电池模型RC参数的辨识问题归结为非线性最优化问题，建立非线性最小二乘优化模型，采用Levenberg⁃Marquard（LM）算法对其进行求解.该优化问题不仅是非线性的，而且非凸，因此需要对优化算法中的初始值进行选取，同时放电电流大小的变化也会影响参数求解结果的稳健性.为解决这两个问题，首次提出一种简单有效的RC参数初始值的选取方法和调整最优化模型中的目标函数的方法，保证该算法在不同放电电流情况下均能得到正确的解.仿真结果表明：在选定合适的初始值的情况下，该算法能够快速准确求解模型中的RC参数值.

关键词： 锂电池 ; 二阶RC等效电路模型 ; 参数辨识 ; 最优化 ; 参数初始值

Abstract

The establishment of an accurate battery model is critical for the estimation of SOC (state of charge) and SOH (state of health).The accuracy of model mainly depends on two aspects: the determination of the model kind and the identification of model parameters. The research shows that the second⁃order dynamic lithium⁃ion battery model can effectively simulate charging and discharging process. So this paper mainly focus on the second⁃order model of lithium battery. The problem of parameters identification of the model can be reduced to a nonlinear optimization problem. Firstly,a corresponding nonlinear least squares optimization model is established. Then the optimal identification results of the parameters are obtained by the Levenberg⁃Marquard algorithm. However the optimization problem is not only non⁃linear,but also non⁃convex. So the selection of the initial value of RC parameters is important to the outcome of the algorithm. At the same time,the variation of the discharge current will also affect the identification results. In order to solve these two problems,this paper first proposes a simple and effective method for selecting the initial value of RC parameters and a method for adjusting the objective function in the optimization model to ensure the algorithm can obtain correct solutions under different discharge current conditions. Parameters under different soc are identified by this method. The simulation results show that the algorithm can quickly and accurately obtain the RC parameter values in the model when a suitable initial value is selected.

Keywords： lithium battery ; second⁃order RC equivalent circuit model ; parameter identification ; optimization ; initial parameter value

PDF (1382KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

吴小慧, 张兴敢. 锂电池二阶RC等效电路模型参数辨识. 南京大学学报（自然科学）[J], 2020, 56(5): 754-761 doi:10.13232/j.cnki.jnju.2020.05.015

Wu Xiaohui, Zhang Xinggan. Parameters identification of second order RC equivalent circuit model for lithium batteries. Journal of nanjing University[J], 2020, 56(5): 754-761 doi:10.13232/j.cnki.jnju.2020.05.015

锂离子电池（简称锂电池）由于具有能量密度高、循环寿命长、无记忆效应、绿色环保等优点，迅速发展成为新一代储能电源^［1-3］.为保证电池储能系统安全、可靠运行，必须基于精确的电池模型建立完善的电池管理系统，对电池状态进行估计和预测^［1］.

目前常用的等效电路模型有Thevenin模型、PNGV模型和多阶RC模型^［3-6］.研究表明，二阶RC网络模型能够较准确地模拟锂电池的各种特性，且将计算量控制在合理的范围内^［1］.对于特定等效电路模型，模型参数辨识方法的好坏直接决定了模型中参数的可靠性和精确度.最小二乘拟合法计算简单，但误差较大^［7-8］；卡尔曼滤波法能得到状态变量的最优估计，但系统噪声的取值会直接影响到辨识的准确性^［9］；遗传算法对全局有较好的辨识精度，但局部搜索能力较差^［10-11］.针对上述问题，本文基于电池二阶模型RC参数关系^［12］建立非线性最小二乘优化模型，采用LM算法^［13-14］求解不同SOC对应的RC参数^［10］.在选定合适的参数初始值的情况下，该方法能够快速且准确地求出模型参数值.

本文首先概述锂电池二阶RC等效电路模型及参数辨识过程，然后基于理想二阶RC电路的恒流放电仿真实验建立相应的最优化模型并求解，最后将完善的参数求解方法应用到实际电池组的参数辨识中，通过仿真验证参数辨识方法的有效性和准确性.

1 锂电池二阶RC模型

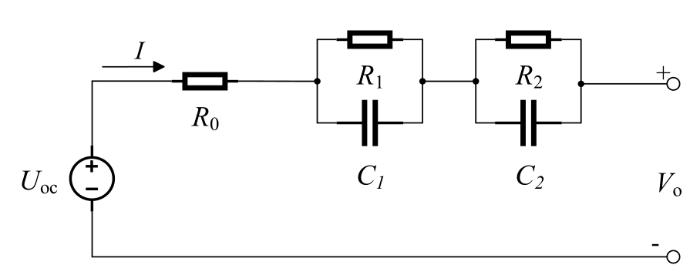
锂电池二阶RC等效电路模型如图1所示，由两个RC网络结构和一个电阻串联构成.图1中，U_OC表示电池的开路电压，R₀表示电池欧姆电阻；R₁和R₂表示电池的极化内阻，C₁和C₂表示电池的极化电容；I表示负载电流；V_O表示可直接测量的电池的端口电压.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 锂电池二阶RC等效电路模型

Fig.1 Second⁃order RC equivalent circuit model of lithium battery

该模型的数学表达式如下所示：

\{\begin{matrix} V_{O} = U_{O C} - U_{1} - U_{2} - I R_{0} \\ I = \frac{U_{1}}{R_{1}} + C_{1} \frac{d U_{1}}{d t} \\ I = \frac{U_{2}}{R_{2}} + C_{2} \frac{d U_{2}}{d t} \end{matrix}

（1）

模型参数辨识问题即依据实验中采集的电流电压数据求解模型中R₀，R₁，R₂，C₁，C₂五个参数值的问题.可从理想二阶RC电路入手，基于电路仿真数据寻找参数的辨识方法，然后将辨识方法用于实际电池的测量数据中，实现对锂电池二阶RC等效电路模型的参数辨识.

2 理想二阶RC电路参数辨识

设定理想二阶RC电路内部参数，进行恒流放电仿真实验，根据仿真数据对RC参数进行辨识，最后将辨识结果与电路设定的参数值进行对比，验证参数辨识方法的可行性.

理想二阶RC电路模型和图1相似，其中U_OC为恒压源E，且R，C的值保持恒定不变.当电路进行恒流放电时有式（2）：

\begin{array}{l} V_{O} (t) = E - I R_{0} - \\ I R_{1} (1 - e^{- \frac{t}{R_{1} C_{1}}}) - I R_{2} (1 - e^{- \frac{t}{R_{2} C_{2}}}) \end{array}

（2）

V_O（0-）~V_O（0+）的变化主要由欧姆电阻R₀上的压降造成，可得式（3）：

R_{0} = (E - V_{O} (1)) / I

（3）

2.1 非线性最小二乘优化模型

基于电路的非线性特性，将R₁，R₂，C₁，C₂的辨识问题转化为非线性最优化问题.由式（2）可知，对于任意的 $X = [R_{1}, R_{2}, C_{1}, C_{2}]$ 参数，任意时刻t都有唯一确定的U_O（t）与之对应，如式（4）所示：

\begin{array}{l} U_{O} (t) = E - I R_{0} - I X (1) (1 - e^{- \frac{t}{X (1) X (3)}}) - \\ I X (2) (1 - e^{- \frac{t}{X (2) X (4)}}) \end{array}

（4）

V_O（t）为电路本身真实的输出电压，可构造如下非线性最小二乘优化模型，如式（5）：

\{\begin{array}{l} m i n F (X) = |U_{O} (t) - V_{O} (t)| \\ s . t . X (1) > 0, X (2) > 0, X (3) > 0, X (4) > 0, t \geq 0 \end{array}

（5）

求解该非线性最小二乘优化模型的全局最优解X，即实现理想二阶RC电路的参数辨识.

2.2 LM优化算法初始值的选取

Levenberg⁃Marquard算法是最优化算法^［15-16］中的一种，通常用于求解非线性最小二乘问题.LM算法求解RC参数的基本思想是根据设定的RC初始值不断迭代寻找出最优的X向量使得F（X）的平方和最小.

该非线性最小二乘问题具有非凸性，LM算法中RC初始值的选取与解的准确性密切相关，不合适的初始值往往收敛较慢，或收敛到非全局最优的局部极小值点.本文提出一种简单快速的初始值选取方法，保证算法求解参数的准确性和高效性.

当电路放电至一定时间，两个电容充满电荷，V_O收敛于一稳定值，如式（6）：

V_{O} (\infty) = E - I (R_{0} + R_{1} + R_{2})

（6）

由式（6）可得R₁、R₂满足的关系式（7）：

R_{1} + R_{2} = R

（7）

其中，

R = (E - V o (\infty)) / I - R_{0}

（8）

对式（2）中的指数项进行泰勒展开，并忽略二阶及以上的项，可得式（9）：

V_{O} (t) \approx E - I R_{0} - I t / C_{1} - I t / C_{2}

（9）

由式（9）可得C₁，C₂及t的关系式（10）：

t / C_{1} + t / C_{2} = C

（10）

其中，

C = (E - I R_{0} - V_{O} (t)) / I

（11）

结合式（7）和式（10），可令R₁=R₂，C₁=C₂，设定LM算法的初始值为：

X_{0} = [R / 2, R / 2,2 t / C, 2 t / C]

（12）

2.3 恒流放电仿真数据

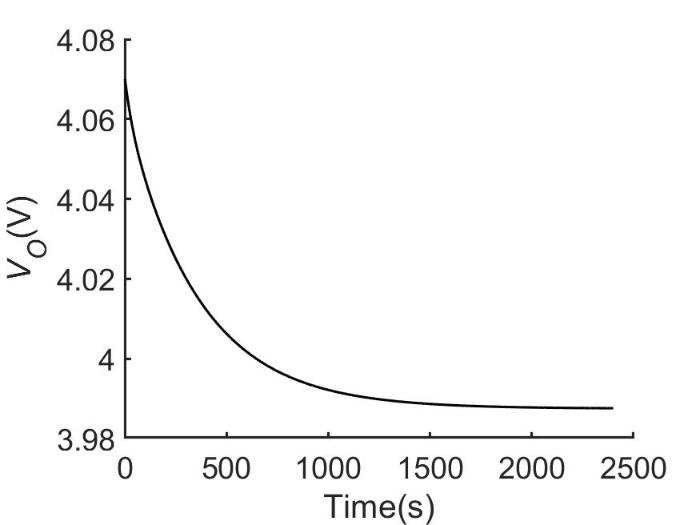
为了获得理想情况下恒流放电的仿真数据，参考单体电池实验数据可对理想二阶电路参数设定如表1所示.输出电压变化过程如图2所示.

表1 理想二阶电路模型参数设定

Table 1 Parameter setting of ideal second⁃order circuit model

电路参数	E(V)	I(A)	R₀(Ω)	R₁(Ω)	R₂(Ω)	C₁(F)	C₂(F)
设定值	4.12	5	0.01	0.015	0.0015	2400	2400

新窗口打开| 下载CSV

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 理想二阶RC电路输出电压仿真数据

Fig.2 Simulation data of ideal second⁃order RC circuit output voltage

根据式（7）、式（10）和式（12），并选定t=10 s（t值可任意），可设定此电路RC参数求解算法中的初始值为：

X_{0} = [0.00825,0.00825,2857.14,2857.14]

（13）

根据上述参数辨识过程在MATLAB中编写实现算法，辨识结果如表2所示.

表2 RC辨识结果

Table 2 RC identification results

参数	R₀(Ω)	R₁(Ω)	R₂(Ω)	C₁(F)	C₂(F)
设定值	0.01	0.015	0.0015	2400	2400
辨识结果	0.01	0.015	0.0015	2400	2400

新窗口打开| 下载CSV

仿真结果表明，RC参数辨识结果与参数设定值完全一致.

2.4 辨识方法验证实验及模型优化

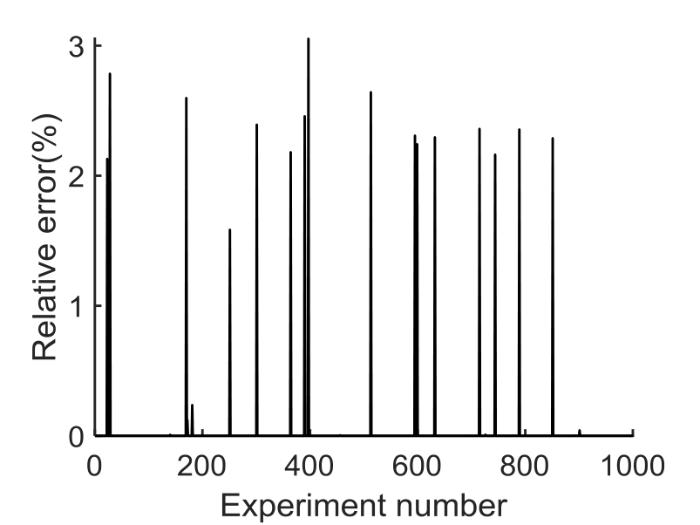
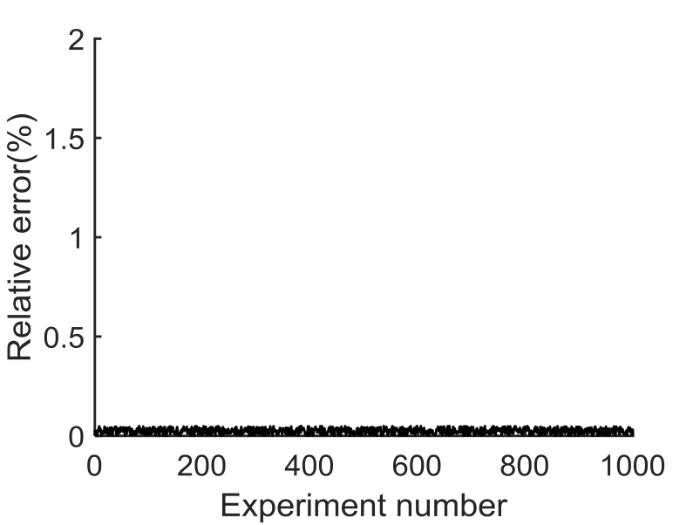
为验证初始值选取方法及辨识方法对于理想二阶RC电路参数求解的通用性和有效性，采用蒙特卡洛方法模拟1000组RC参数辨识仿真实验，在参数设定符合电池实际情况的前提下，随机设定二阶RC电路模型的电源电压值、放电电流值以及电路的RC参数值进行恒流放电仿真实验.不同情况下参照2.2节参数初始值的选取方法确定RC初始值，通过算法对电路模型中的RC参数进行求解，计算每组实验的参数辨识结果和电路参数设定值的相对误差，实验结果如图3所示，横轴为实验序号，纵轴表示参数辨识结果的相对误差之和.

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 随机实验参数辨识结果

Fig.3 Identification results of random experimental parameters

分析实验结果发现对于RC参数估算结果误差百分比较大的情况，电路放电电流值都比较小.进行随机小电流恒流放电实验（图4）.

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 随机实验参数辨识结果

Fig.4 Identification results of random experimental parameters

仿真结果证明放电电流较小时RC参数求解结果的误差普遍较大.计算目标函数F（X）的雅可比矩阵发现，F（X）的大小和放电电流值成正比，当I较小时算法将提前达到终止条件，无法得到RC参数的全局最优解.针对该问题，对最优化模型中的目标函数F进行如下调整，如式（14）：

m i n F (X) = |(U_{O} (t) - V_{O} (t)) / I|

（14）

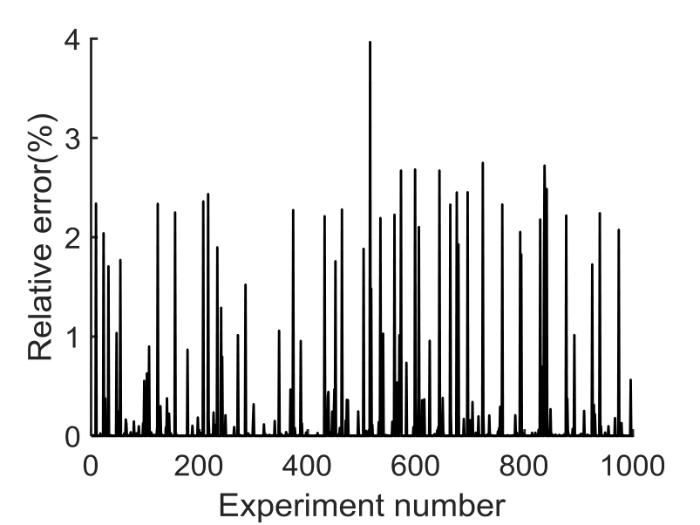
改进后的最优化模型与原模型同解，目标函数的雅克比矩阵中不再含有电流项，可避免小电流对梯度的影响.同样再次进行1000次蒙特卡洛实验（图5）.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 随机实验参数辨识结果

Fig.5 Identification results of random experimental parameters

实验结果显示较大的误差项全部消失，每次实验都得到了最优解，证明了新模型的稳定性.

3 实测数据验证

本文实验对象为LF55K电池组，该电池组由16节相同的单体电池先串联后并联组成，电池组标称容量为55 AH，实验环境温度为恒温25 ℃.在不考虑电池组内部单体电池相互影响的情况下，可将电池组看成一个大的单体锂电池，同样可选用二阶RC等效电路模型模拟电池组特性.锂电池二阶RC等效电路与理想二阶电路的电路特性有所不同，需对电池特性进行分析后才能合理使用上述参数辨识方法.

3.1 特性测试实验

3.1.1 SOC⁃U_OC标定实验

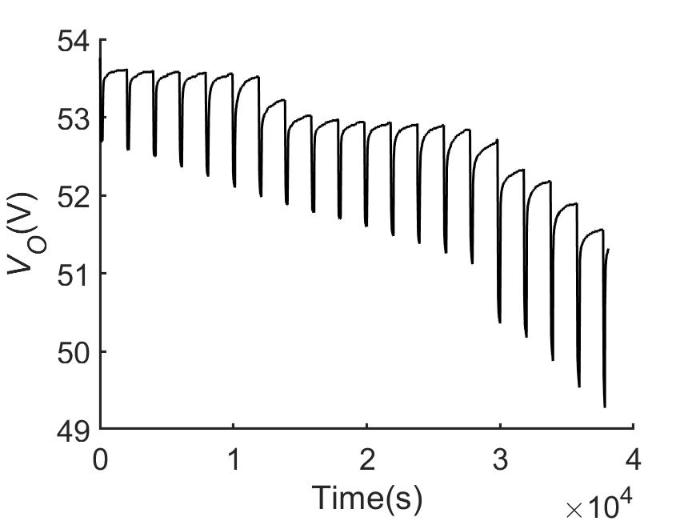
锂电池的内部参数时刻变化，不同SOC下RC参数的辨识需要对应的开路电压值.为得到SOC和U_OC之间的关系，对电池进行脉冲放电实验：在电池充满电荷的情况下，以55 A电流脉冲放电，每放电5%SOC后停止放电，将电池静置至平衡状态（图6）.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 锂电池组脉冲放电实验

Fig.6 Pulse discharge experiment of lithium battery pack

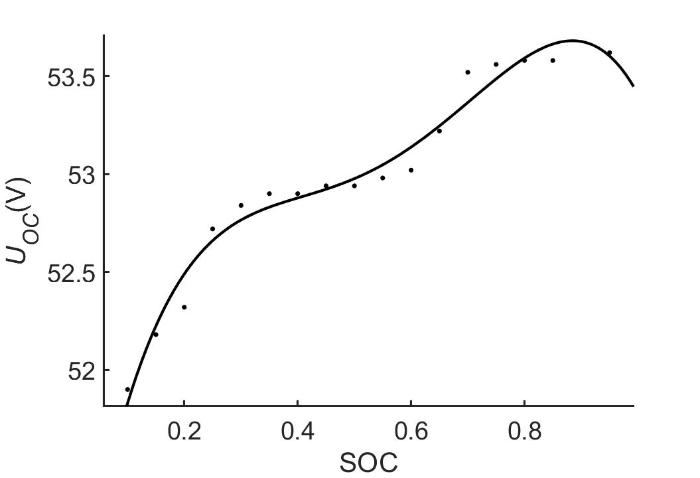
电池静置后测量的端电压值即当前SOC对应的U_OC值，对数据进行最小二乘法拟合，可得SOC与U_OC的关系曲线（图7）.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 SOC⁃U_OC关系曲线

Fig.7 SOC⁃U_OCrelationship curve

3.1.2 回弹特性

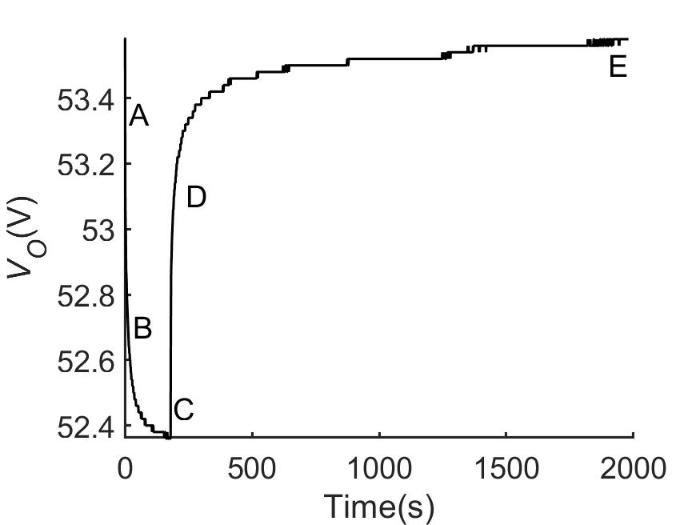
充放电结束后化学反应不会立刻停止，对外表现为端电压迅速上升后逐渐趋于一个稳定值，即电池的“回弹特性”.图8为脉冲放电实验中某单个脉冲放电全过程V_O的变化曲线.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 电池端电压变化曲线

Fig.8 Battery terminal voltage change curve

A点为电池开始放电时刻，C点为放电结束时刻，整个过程可分为以下四个阶段.

AB段：电路开始放电，端口电压迅速下降，这主要是受欧姆电阻R₀的影响.

BC段：由于电池内部的极化特性的影响，端口电压缓慢下降，该段可近似为零状态响应，Vo如式（15）.

\begin{array}{l} V_{O} (t) = U_{O C} (s o c) - I R_{0} (s o c) - \\ I R_{1} (s o c) (1 - e^{- \frac{t}{R_{1} (s o c) C_{1} (s o c)}}) - \\ I R_{2} (s o c) (1 - e^{- \frac{t}{R_{2} (s o c) C_{2} (s o c)}}) \end{array}

（15）

CD段：AB段的一个逆过程，D点为电池放电结束的下一时刻，D点电压如式（16）.

V_{O} (t_{D}) = U_{O C} (s o c) - I R_{1} (s o c) - I R_{2} (s o c)

（16）

DE段：该段表示电池的“回弹特性”，E点表示电池已静置至稳定状态.该过程可近似为电路的零输入响应，V_O如式（17）.

\begin{array}{l} V_{O} (t) = U_{O C} (s o c) - I R_{1} (s o c) e^{- \frac{t}{R_{1} (s o c) C_{1} (s o c)}} - \\ I R_{2} (s o c) e e^{- \frac{t}{R_{2} (s o c) C_{2} (s o c)}} \end{array}

（17）

3.2 内部参数辨识

通过3.1中的特性分析，可根据AB段和CD段求解R₀，如式（18）：

\begin{array}{l} R_{0} (s o c) = (V_{O} (t_{A}) - V_{O} (t_{B})) / I = \\ (V_{O} (t_{D}) - V_{O} (t_{C})) / I \end{array}

（18）

根据回弹阶段（DE段）电压、电流数据建立非线性最小二乘优化模型，目标函数如（14）式所示，对当前SOC对应的R₁，R₂，C₁，C₂参数进行辨识.根据式（16）和式（17）可得R，C的关系（式（19）和式（20））：

R_{1} (s o c) + R_{2} (s o c) = \frac{U_{O C} (s o c) - V_{O} (t_{D})}{I}

（19）

\begin{array}{l} \frac{1}{C_{1} (s o c)} + \frac{1}{C_{2} (s o c)} \approx \\ \frac{V_{O} (t) - (U_{O C} (s o c) - I (R_{1} (s o c) + R_{2} (s o c)))}{I t} \end{array}

（20）

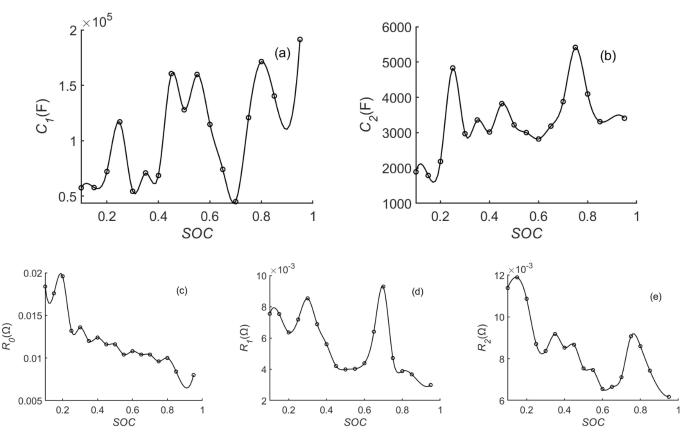
结合实验中实测数据，利用R，C满足的关系式确定不同SOC下参数求解算法的初始值，可离线辨识得到不同SOC对应的RC参数值，通过三次样条插值，可分别得到R，C关于SOC的变化曲线（图9）.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 不同SOC下RC辨识结果

Fig.9 Model parameters of battery under different SOC

3.3 辨识结果正确性验证

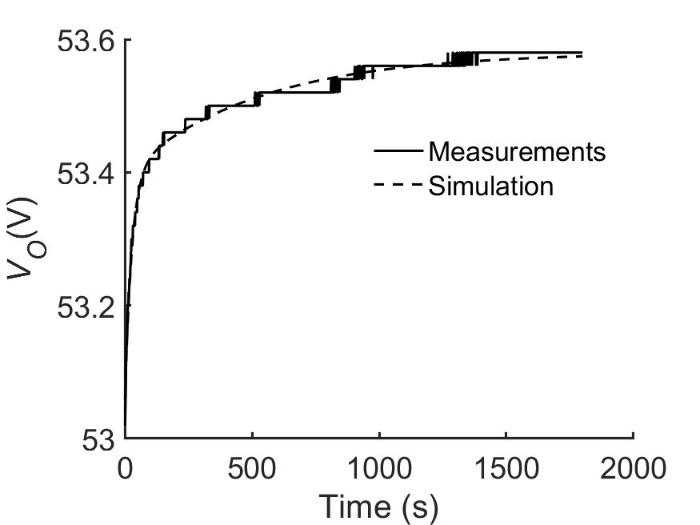
为验证参数辨识结果的正确性，可将辨识结果代入电路模型中进行仿真实验，在同等条件下，将端口电压仿真值和实测值进行比较.回弹特性阶段验证结果如图10所示.

图10

新窗口打开| 下载原图ZIP| 生成PPT

图10 回弹特性曲线

Fig.10 Rebound characteristic curve

根据仿真结果计算可得，该锂电池组电压回弹过程中，仿真值和实测值的绝对误差最大值为0.039 V，平均误差为0.008 V，相对误差不超过0.074%.

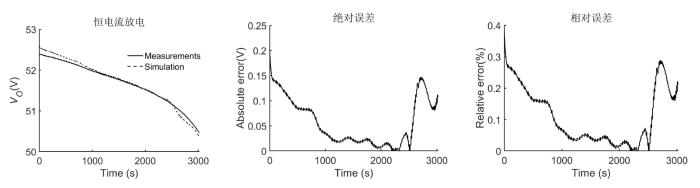
为验证所有辨识结果，对电池组进行恒流放电验证实验：将动力电池组充满电，静置电池组至稳定状态，以55 A电流放电3000 s，记录端口电压值.基于3.2中求得的R，C关于SOC的曲线关系，当系统运行时根据实时的SOC值更新模型对应的RC参数，实时计算端口电压的仿真值，整个过程仿真值和实测值的对比见图11.

图11

新窗口打开| 下载原图ZIP| 生成PPT

图11 仿真值和实测值对比

Fig.11 Comparison of simulated and measured values

仿真结果显示，整个放电过程仿真值和实测值的最大绝对误差为0.203 V，平均误差为0.057 V，平均相对误差为0.111%.

综合以上分析可知，在选定合适的参数初始值的情况下，基于非线性最小二乘优化模型的RC参数求解方法能够快速精确地辨识出电池组中的RC参数.

4 结论

本文针对锂电池二阶RC等效电路模型建立非线性最小二乘优化模型，采用LM算法对RC参数进行求解，着重研究了求解算法参数初始值的选取方法及解关于放电电流变化的稳定性问题，提出初始值选取时需要满足的两个关系式，并对优化模型中的目标函数进行调整，保证了解的正确性和稳健性.通过该方法可简单快速且精确地辨识实际电池不同SOC状态下的RC参数值.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

李玲慧

电池管理系统的研究与设计

硕士学论文.天津:天津大学,2014. (Li L H Research and Design of Battery Management System. Master' Dissertation. Tianjin: Tianjin University,2014

[本文引用: 3]

[2]

张东华，马燕，陈思琪等.

锂电池模型参数估计与荷电状态估算研究

武汉理工大学学报(信息与管理工程版)，2015，37（2）：179-182.

Zhang

D H

,Ma

,Chen

S Qet al

Parameter analysis method for lithium-ion battery circuit model and state of charge estimatio

Journal of Wuhan University of Technology(Information & Management Engineering),2015,37(2): 179-182.

[3]

,Cheng

X M

A comparative study on RC models of lithium⁃ion battery

∥2014 IEEE Conference and Expo Transportation Electrification Asia⁃Pacific (ITEC Asia⁃Pacific). Beijing,China: IEEE,2014:1-4.

[本文引用: 2]

[4]

Cheng

,Zhou

Y M

,Song

Z B

,et al.

Modeling and SOC estimation of LiFePO4 battery

∥2016 IEEE International Conference on Robotics and Biomimetics (ROBIO). Qingdao,China: IEEE,2016:2140-2144

[5]

Birkel

C R

,Howey

D A

Model identification and parameter estimation for LiFePO₄ batteries

∥IET Hybrid and Electric Vehicles Conference 2013 (HEVC 2013). London,UK: IET Press,2013:1-6.

[6]

李哲

纯电动汽车磷酸铁锂电池性能研究

.博士学论文.北京:清华大学,2011.