Journal of Nanjing University(Natural Sciences) >

2021 , Vol. 57 >Issue 6: 1075 - 1082

DOI: https://doi.org/10.13232/j.cnki.jnju.2021.06.016

A FPGA⁃based convolutional neural network training accelerator

  • Hao Meng 1, 2 ,
  • Qiang Liu , 1, 2
Expand
  • 1. School of Microelectronics，Tianjin University, Tianjin，300072，China
  • 2. Tianjin Key Laboratory of Imaging and Sensing Microelectronics Technology，Tianjin，300072，China

Received date: 2021-05-31

  Online published: 2021-12-03

Fold

Highlights

In recent years，convolutional neural networks have been widely used in image classification and image segmentation tasks. Convolutional neural network training accelerator based on FPGA (Field Programmable Gate Array) has the problems of low weight gradient calculation efficiency and high resource occupation of the adder. A high⁃performance convolutional neural network training accelerator is designed in this paper. Firstly，we propose a convolutional single⁃engine architecture which adds an additional self⁃accumulation unit based on the inference accelerator. The accelerator supports the forward propagation and back propagation (error back propagation and weight gradient calculation) of the convolutional layer to improve the reusability and the efficiency of weight gradient calculation at the same time. Then we design a novel adder tree which supports the kernel adder tree and self⁃accumulation units. Finally，the proposed training accelerator is implemented on the Xilinx Zynq xc7z045 platform to train VGG⁃like (Visual Geometry Group) network model on the CIFAR⁃10 dataset. Experimental results show that at a clock frequency of 200 MHz，the 8⁃bit fixed⁃point training accelerator achieves an average performance of 64.6 GOPS (Giga Operations per Second). Its average performance is 9.36 times higher than that of Intel Xeon E5⁃2630 v4 CPU (Central Processing Unit) training platform，and its energy efficiency is 17.96 times higher than that of NVIDIA Tesla K40C GPU (Graphics Processing Unit) training platform.Compared with several existing FPGA accelerators，the proposed accelerator has advantages in performance and storage resource usage.

Cite this article

Hao Meng , Qiang Liu . A FPGA⁃based convolutional neural network training accelerator[J]. Journal of Nanjing University(Natural Sciences), 2021 , 57(6) : 1075 -1082 . DOI: 10.13232/j.cnki.jnju.2021.06.016

卷积神经网络（Convolutional Neural Network，CNN）是深度学习的代表算法之一，在目标检测［1］、物体识别［2］和语音识别［3］等领域广泛应用.在现有应用方案中，CNN模型主要在云端完成训练，在终端执行推理.为了适应具体的应用场景，终端需要向云端上传海量数据来对模型进行重新训练以及时更新参数，这会带来巨大的网络传输带宽压力及数据隐私泄露的问题，解决上述问题的一个有效方案是实现在边缘计算设备端的在线学习.现有的训练平台主要有中央处理器（Central Processing Unit，CPU）、图形处理单元（Graphics Processing Unit，GPU）、专用集成电路（Application Specific Integrated Circuit，ASIC）和现场可编程门阵列（Field Programmable Gate Array，FPGA）.其中CPU采用流程控制模式，计算效率低；GPU拥有大量计算核心，但是存在功耗过大的问题；ASIC是一种完全定制化硬件，性能最好，但设计和制造周期长.FPGA作为一种高速半定制化硬件，具有能效高和硬件架构设计灵活的优势，成为在能源有限的边缘计算端实现训练加速器的理想平台.
现有的基于FPGA的深度神经网络加速器主要用于网络模型的推理［4-9］.低位宽量化［10-13］、剪枝［14-15］技术可用来降低深度神经网络的计算和空间复杂度，但是推理加速器无法直接用于高效的深度神经网络训练.这是由于：（1）训练过程更复杂，计算量是推理的五倍以上［16］；（2）训练过程包含与推理操作不同的反向传播操作，如超大核卷积、矩阵转置、函数求导等.因此，需要根据训练算法的特点，设计一个高效的训练加速器.同时，为了适应边缘端的资源限制，加速器应能同时支持推理和训练.现有的FPGA训练加速器从计算单元结构、访存方式等多个方面提出CNN训练硬件加速方案，但是要么难以满足应用的算力需求，要么所需存储空间过大.Zhao et al［17］提出F⁃CNN可配置训练框架，在运行时通过重新配置数据流路径，覆盖CNN的各层训练任务；Liu et al［18］采用统一的计算引擎和可扩展框架，设计了一种基于FPGA的训练加速器.上述两种硬件加速方案基于卷积计算架构均获得了不错的加速效果，但是都没有对卷积权重梯度计算涉及的超大核卷积进行优化，存在性能提升空间.Fox et al［19］和Luo et al［20］将网络每一层的卷积操作转变为通用矩阵乘操作，可以适应不同尺寸的卷积运算，但是这种方案需要引入一个预处理操作，将输入数据重组为矩阵列，存在所需片上存储过大或者存储带宽需求过大的问题.此外，训练过程中，卷积神经网络正向传播和反向传播需要不同类型的累加操作，分别设计相应累加器的方案虽然简单，但是需要大量的加法器，在计算并行度大的情况下会耗费较多的计算资源.
针对上述问题，采用可重构的设计方法，本文使用软硬件协同的工作模式对卷积神经网络训练进行加速.基于卷积计算架构的设计思路，本文提出一种卷积神经网络训练加速器，不仅可以支持卷积层的正向传播和反向传播，还实现了权重梯度计算的优化.同时，提出一种可配置的新型加法树设计，兼容卷积核内加法树和自累加单元，减少加速器的资源消耗.提出的设计方法为在低功耗边缘设备端实现在线学习提供了解决方案.

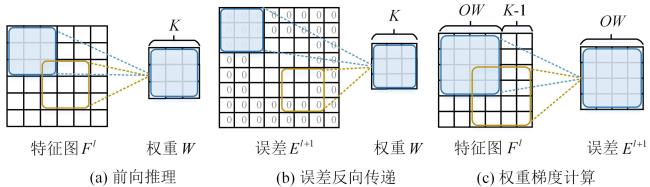
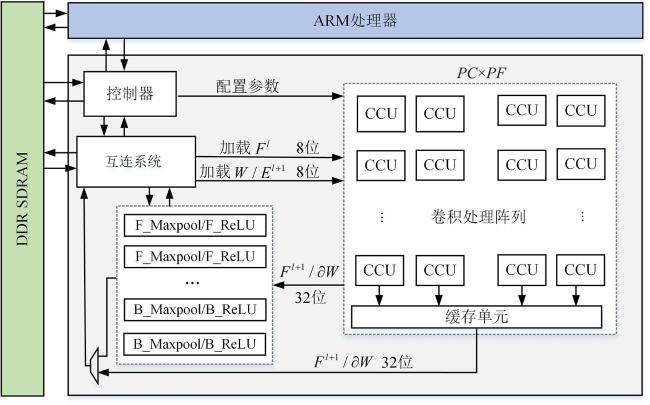
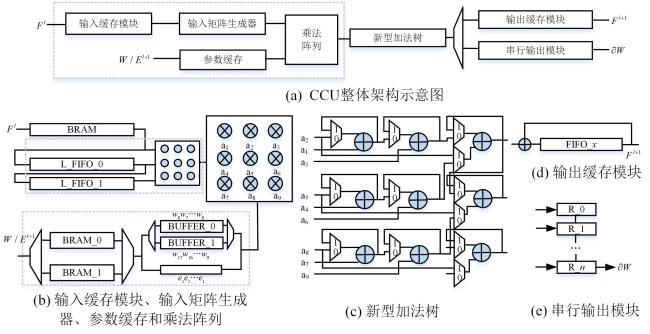
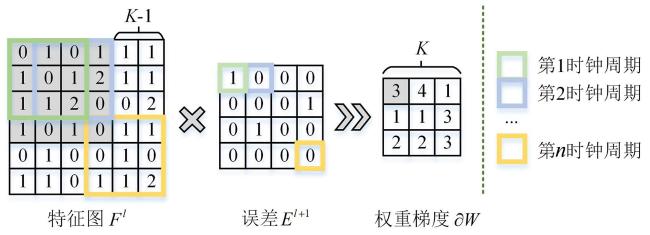
1 卷积神经网络训练算法

卷积神经网络训练包括四个步骤：前向推理、误差反向传递、权重梯度计算以及权重更新.在线训练需要实现这四个步骤的多次迭代，以找到模型的本地个性化最佳的权重梯度.
在CNN中，卷积层是整个网络结构的核心，也是计算量最大、最耗时的部分.其前向推理过程将输入特征图Fl与权重W进行卷积计算，生成下一层的输入特征图Fl+ 1，如式（1）所示：
F i l + 1 = ∑ j = 1 N c F j l ⊗ W i j
式中， ⊗代表卷积操作，N c代表特征图Fl的通道数.误差反向传递使用损失函数计算误差，然后将误差El +1与权重W进行卷积计算，将误差传递到上一层，获得误差El，如式（2）所示：
E j l = ∑ i = 1 N f E i l + 1 ⊗ W i j R
式中，N f代表误差El +1（特征图Fl+ 1）的通道数，R代表转置操作.权重梯度计算将特征图Fl和误差El +1进行卷积计算，完成权重梯度 ∂ W的计算，获取所有权重梯度，如式（3）所示：
∂ W i j = F j l ⊗ E i l + 1
权重更新根据学习率η和权重梯度对权重进行修正，如式（4）所示：
W = W - η ⋅ ∂ W
图1展示了卷积层的前向推理、误差反向传递和权重梯度计算的卷积具体操作，其中前向推理和误差反向传递的卷积尺寸均为K（K一般为3）；但是误差反向传递计算中，额外增加了对误差El +1的零填充（Zero Padding）操作以及对权重的转置操作R.在权重梯度计算中，由于每层的误差El +1的尺寸不完全一致，导致其卷积尺寸（OW）不固定，给整体训练架构的硬件实现带来了一定的难度.因此，对权重梯度计算进行优化，设计一款灵活高效的可配置卷积计算单元是设计高效训练架构的关键.
图1 正向传播和反向传播过程中的卷积操作

Fig.1 Convolution operation during forward propagation and back propagation

除卷积层外，卷积神经网络还包含全连接层、批归一化层、池化层和非线性层等.其中，全连接层的正向传播和反向传播与卷积层类似，不同之处在于其采用点乘操作代替卷积操作.批归一化层的正向传播是对输入特征图Fl进行归一化处理，再通过尺度变化因子γ及偏移项β对标准化后的数据进行线性变换.反向传播需要对输入特征图、尺度变化因子γ及偏移项β进行求导，较复杂，一般在软件上执行.池化层的正向传播是将同一特征图的相邻神经元汇总输出，进行特征降维.非线性层的正向传播是使用线性修正单元（Rectified Linear Unit，ReLU）等函数将像素值限制在合理的范围内.池化层和非线性层的反向传播仅需对输入特征图求导.

2 加速器设计及优化

2.1　卷积单引擎架构设计

为了能最大限度地提高硬件资源利用率，进一步提高加速器的通用性，本文采用软硬件协同的工作模式，利用处理器对卷积计算引擎进行实时配置，提出一款可兼容卷积的正向传播和反向传播的加速器架构.基于Zynq系列FPGA平台的加速器整体架构如图2所示.该架构中，ARM处理器（Advanced RISC Machine，ARM）作为整个系统的控制端，发出指令控制整体数据流的计算方式，通过互连系统配置卷积计算引擎的工作模式、输入尺寸、特征图通道数等.此外，ARM处理器还负责完成量化及数据预处理等对计算性能要求不高的操作，例如将特征图Fl、权重W以及误差El +1量化至定点8位.卷积计算引擎通过配置可实现前向推理、误差反向传递和权重梯度计算三种不同的功能，包含PC×PF个卷积计算单元（Convolution Calculation Unit，CCU），PC代表卷积核通道方向并行度，PF代表卷积核个数方向并行度.此外，卷积计算引擎还包含池化正反向（F/B_Maxpool）、非线性单元正反向（F/B_ReLU）等模块.卷积计算处理后，输出数据位宽为32位，通过互连系统传回至双倍速率同步动态随机存储器（Double Data Rate SDRAM， DDR SDRAM）中.
图2 加速器的整体架构

Fig.2 The overall architecture of the accelerator

该软硬件协同设计的训练加速器可以通过多次配置卷积计算引擎匹配不同卷积层的正反向传播操作，实现对多种CNN网络模型的训练.下文主要介绍卷积计算引擎中的CCU卷积计算单元的设计优化.

2.2　权重梯度计算优化

本文提出的CCU卷积计算单元不仅可以支持前向推理和误差反向传递中的标准卷积，还可以支持权重梯度计算的超大核卷积，并且对超大核卷积操作进行了优化.CCU卷积计算单元整体架构如图3a所示，图3b至图3e为CCU中具体模块的示意图，主要包括输入缓存器、输入矩阵生成器、参数缓存（权重W和误差El+ 1）、乘法单元、新型加法树（同时支持卷积核内加法树和自累加单元）、输出缓存器和串行输出模块.
图3 卷积计算单元的具体模块

Fig.3 Specific modules of CCU

为了提高权重梯度计算效率，在推理架构的基础上对参数缓存模块进行改进，采用两个片上存储器（BRAM_0，BRAM_1）和两个缓存器（BUFFER_0，BUFFER_1）接收片外传输的权重W和误差El+ 1数据，并将其拼接成不同训练操作所需的形式.如图3b所示，在前向推理和误差反向传递中，需要将权重W拼接成 K × K的权重矩阵（如 w 8 w 7 … w 0和 w 17 w 16 … w 9）；在权重梯度计算中，需要将每周期读取的误差El+ 1复制成 K × K的误差矩阵（如 e 1 e 1 … e 1）.两个片上存储器和两个缓存器用于节约缓冲区的空间及提高数据的传输效率.传入一部分权重W或者误差El+ 1后，利用输入缓存器和输入矩阵生成器将数据拼接成 K × K的输入矩阵.之后根据不同的模式需求，通过乘法阵列和新型加法树（图3c）对权重矩阵/误差矩阵和输入矩阵做乘累加运算，将累加的结果分别传送至输出缓存模块（图3d）或者串行输出模块（图3e），完成前向推理、误差反向传递或者权重梯度计算.其中，输出缓存模块在前向推理和误差反向传递中用于缓存计算的中间结果；串行输出模块将权重梯度并行计算后的结果转换为低位宽进行输出.在前向推理和误差反向传递中，权重拼接的时间与乘累加运算的时间可以重叠计算；在权重梯度计算中，乘累加运算的时间和梯度传出的时间可以重叠计算.
在权重梯度计算中，卷积尺寸的大小由误差El+ 1的尺寸决定，误差El+ 1的尺寸大小与每层的输出特征图相同.由于池化层的存在，所有层的输出特征图尺寸并不一致，这成为高效硬件训练加速器设计的主要挑战之一.本文提出的CCU卷积计算单元中，通过一个 K × K的滑动窗口将特征图Fl分为若干个小区域，将每个周期滑动窗口内的所有数据同时与对应的误差El+ 1的数据做乘法.如图4所示，第一时钟周期，特征图Fl中第一个 K × K的窗口与误差El+ 1的第一个数据同时做乘法；第二时钟周期，特征图Fl中第二个 K × K的窗口与误差El+ 1的第二个数据同时做乘法；以此类推，将所有时钟周期获得的乘法结果进行对应位置的累加，同时获取 K × K个权重梯度.其中，特征图Fl与误差El+ 1存在固定尺寸差 K - 1.这种硬件架构设计不仅将权重梯度计算中不固定的卷积尺寸转化为固定的卷积尺寸 K × K，还额外实现了 K × K P K倍的并行度.
图4 权重梯度计算及其优化

Fig.4 Calculation and optimization of weight gradient

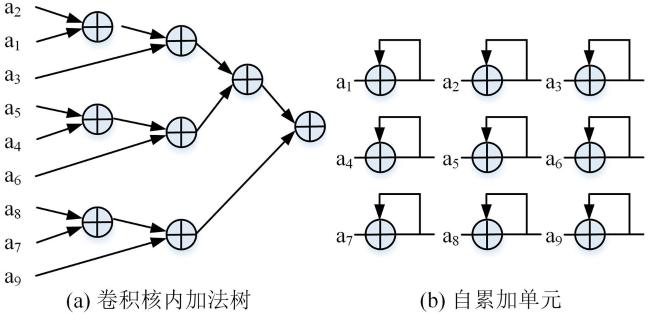
2.3　新型加法树优化

目前大部分加速器设计主要针对乘法单元进行优化，对加法器单元优化的研究较少.2.2中为了适配CCU卷积计算单元的不同工作模式，需要设计不同类型的累加形式.在前向推理和误差反向传递模式下，需要实现卷积窗口内数据的累加（卷积核内加法树）.如图5a所示，该累加形式由八个加法器构成一个四级加法树，对九个乘法器的输出进行累加.在权重梯度计算模式下，需要实现本周期数据与上一周期数据的累加（自累加单元）.如图5b所示，该累加形式由九个加法器构成.两者的输入位宽均为16位（乘法阵列的输出位宽），累加输出位宽为32位.分别设计两种累加形式的方案虽然简单，但是在并行度大时需要使用大量的加法器，耗费加法器的资源.针对上述弊端，本文设计了如图3c所示的可配置的新型加法树，兼容两种累加形式，在加法器资源上进行复用，进一步节约了加法器所耗费的计算资源.这种设计下，以单个卷积核窗口大小为例，优化前共需要17个加法器，优化后仅需九个加法器.
图5 新型加法树的累加形式

Fig.5 The accumulation mode of new adder tree

3 实验结果及分析

实验平台采用Xilinx Zynq xc7z045 FPGA，包含处理系统（Processing System，PS）和可编程逻辑（Programmable Logic，PL）两部分.本文主要在硬件上实现了卷积层（全连接层）、池化层和非线性层的正反向传播.所有实验结果都是布局布线后的实验结果.

3.1　实验模型

本文比较了FPGA平台上各类低精度训练技术的优缺点，综合训练精度、面积和功耗的考虑，参考Banner et al［12］的量化方案对卷积神经网络进行压缩训练，同时将误差El +1量化至8位参与权重梯度计算.选择VGG⁃like网络模型和CIFAR⁃10数据集对训练加速器进行实验评估与分析，网络不同层的参数如表1所示，通过重复配置卷积计算引擎完成整个网络的训练.在定点8位量化方案下，其训练精度与单精度浮点训练方案相比仅下降0.56%.
表1 VGG⁃like网络模型结构

Table 1 The structure of VGG⁃like network model

层 通道数 卷积核数 输出高宽 卷积核
卷积1 3 128 32×32 3×3
卷积2 128 128 32×32 3×3
池化 128 128 16×16 2×2
卷积3 128 256 16×16 3×3
卷积4 256 256 16×16 3×3
池化 256 256 8×8 2×2
卷积5 256 512 8×8 3×3
卷积6 512 512 8×8 3×3
池化 512 512 4×4 2×2
全连接 8192 1024 - -
全连接 1024 10 - -

3.2　资源使用情况

选择FPGA嵌入式数字信号处理（Digital Signal Processing，DSP）单元实现乘法器，采用可编程逻辑资源（查找表Look Up Table，LUT）、触发器（Flip⁃Flop，FF））实现加法器.本文提出的加速器共需 P C × P F × P K个DSP单元（一个乘法器对应一个DSP单元）.由于卷积神经网络中数据是在层与层之间进行传递的，上一层的输出方向并行度正是下一层的输入方向并行度.在设计中采用 P C = P F的并行方案可以减少数据排列转换的操作，更有利于硬件实现.由于片上共有900个DSP资源，选择 P C = 8， P F = 8 , P K = 9的并行方案实现加速器.加速器的资源使用情况如表2所示.训练加速器共消耗25.03%的LUT资源、17.03%的FF资源、24.68%的块存储器（Block RAM，BRAM）资源及68.33%的DSP资源.BRAM的大小为36 kb.本文硬件设计在200 MHz的时钟频率下进行评估.
表2 加速器资源使用情况

Table 2 Resource usage of accelerators

LUT FF BRAM DSP
总资源数 218600 437200 545 900
占用资源数 54725 74458 134.5 615
使用率 25.03% 17.03% 24.68% 68.33%

3.3　加法树资源使用对比

为了评估提出的加法树设计方法，本文对 P C = 1， P F = 1和 P C = 8， P F = 8两种条件下消耗的加法器资源进行实现对比.实验结果如表3所示，优化后的加法树在 P C = 1， P F = 1时消耗的LUT资源减少到原来的82.3%，消耗的FF资源减少到原来的45.3%；在 P C = 8， P F = 8时（额外包含通道方向并行度的累加），消耗的LUT资源减少到原来的81.8%，消耗的FF资源减少到原来的46.7%.
表3 加法树资源使用对比

Table 3 Resource usage of addition trees

L U T , F F 优化前 优化后 优化比例
卷积核内加法树 自累加单元 合计
P C = 1 , P F = 1 257,388 480,680 737,1068 607,484 82.3 % , 45.3 %
P C = 8 , P F = 8 18264,26648 30720,43520 48984,70168 40064,32792 81.8 % , 46.7 %

3.4　与CPU和GPU平台的对比

本实验采用的CPU和GPU实验平台如表4所示，采用单精度浮点进行训练.对比分别在三个平台上使用单张图片训练VGG⁃like网络的性能（迭代次数为1，批大小为1），结果如表4所示.由于本文的硬件设计主要针对卷积层、池化层、非线性层及全连接层，因此在三个平台上进行性能评估时仅包含上述各层操作，其中FPGA的功耗为Vivado布局布线后的功耗分析结果.由表可见，本文提出的加速器性能是Intel Xeon E5⁃2630 v4 CPU训练平台的9.36倍，能效是NVIDIA Tesla K40C GPU训练平台的17.96倍.
表4 CPU，GPU和FPGA的性能比较

Table 4 Performance of CPU,GPU and FPGA

参数 CPU GPU FPGA
平台 Intel Xeon E5⁃2630 v4

NVIDIA

Tesla K40C

 Xilinx Zynq xc7z045
工艺(nm) 14 28 28
频率(GHz) 2.2 0.745 0.2
精度 32位浮点 32位浮点 8位定点
每批训练时长(ms) 539.97 13.62 57.60
功耗(W) 85 245 3.21
操作性能(GOPS) 6.9 273.3 64.6
能效(GOPS·W-1) 0.08 1.12 20.12

3.5　与现有FPGA加速器的对比

表5展示了本文提出的加速器与现有的FPGA加速器在资源、功耗和操作性能等方面的对比，表中黑体字表示指标最优.由表可见，由于网络模型不同，不同训练加速器呈现不同的性能.为了便于对比，评价指标采用资源使用效率（DSP使用效率GOPS/DSP，BRAM使用效率GOPS/BRAM）和能效（GOPS·W-1）.Zhao et al［17］，Liu et al［18］与本文均采用卷积计算架构对卷积神经网络训练进行加速设计.Zhao et al［17］采用八张Altera Stratix V板卡对AlexNet性能进行评估，本文的DSP使用效率是其3.75倍.与Liu et al［18］相比，本文的DSP使用效率是其8.75倍，BRAM效率是其4.8倍，能效是其15.9倍.Fox et al［19］和Luo et al［20］将卷积计算转换为矩阵乘法，利用高级综合生成相应的矩阵乘法单元.与Fox et al［19］相比，其DSP使用效率是本文的1.8倍，但是本文的BRAM使用效率是其2.4倍.由于使用更先进的FPGA器件，Luo et al［20］的DSP使用效率和能效在几个加速器中都是最高的，但是本文的BRAM使用效率是其1.6倍.
表5 不同FPGA训练加速器性能对比

Table 5 Performance of different FPGA training accelerators

加速器 平台

模型

数据集

数据

类型

DSP/LUTs/

FFs/BRAM

功耗

(W)

操作性能

(GOPS)

DSP使用效率

(GOPS/DSP)

 BRAM使用效率(GOPS/BRAM)

能效

(GOPS·W-1)
Zhao et al[17]

Altera

Stratix V

AlexNet

-

单精度

浮点

≈2214/-/

-/-

 - 62.06 0.028 - -
Liu et al[18]

Xilinx

ZU19EG

LeNet⁃5

CIFAR⁃10

单精度

浮点

1500/329.3 k/

466.0k/174

 14.24 17.96 0.012 0.10 1.26
Fox et al[19]

Zynq

ZCU111

VGG16

CIFAR⁃10

8位

定点

1037/73.1 k/

25.6 k/1045

 - 205 0.19 0.20 -
Luo et al[20]

UltraScale+

XCVU9P

VGG⁃like

CIFAR⁃10

8位

定点

4202/480 k/

-/≈4717

 13.5 1417 0.33 0.30 104.9
本文

ZC706

Xc7z045

VGG⁃like

CIFAR⁃10

8位

定点

615/54.7 k/

74.5 k/134.5

 3.21 64.6 0.105 0.48 20.1

≈：根据文献中数据转换为本文器件的相应资源.

与上述加速器的对比可以发现，本文提出的加速器实现了性能和资源使用效率的折中，为在资源受限的边缘设备端实现CNN训练提供了解决方案.

4 结 论

本文基于嵌入式FPGA设计了一款高性能卷积神经网络训练加速器，通过优化权重梯度计算和加法树设计实现性能和资源使用效率的折中.实验结果表明，提出的加速器性能是Intel Xeon E5⁃2630 v4 CPU训练平台的9.36倍，能效是NVIDIA Tesla K40C GPU训练平台的17.96倍，与现有的FPGA训练加速器相比在性能和存储资源方面有优势.这款训练加速器为在边缘设备端实现卷积神经网络训练提供了可行性方案.
目前本文的设计方案主要针对卷积核大小为3×3的卷积神经网络，后续考虑对现有结构做进一步优化，支持其他网络中可能出现的卷积核大小为1×1和5×5的情况，提高加速器的通用性和灵活性.此外，实验表明，批归一化在训练时间中的占比可达10.3%~14.1%，为进一步提升加速器性能，未来将对批归一化层进行硬件加速设计.

References

Publishing order | Descend order by publishing year | Descend order by cited within
1
Redmon J， Farhadi A. YOLO9000：Better，faster，stronger∥Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu，HI，USA：IEEE，2017：6517-6525.

2
Russakovsk O， Deng J， Su H，et al. ImageNet large scale visual recognition challenge. International Journal of Computer Vision，2015，115(3)：211-252.

3
Zhang Y， Chan W， Jaitly N. Very deep convolutional networks for end⁃to⁃end speech recognition∥Proceedings of the IEEE International Conference on Acoustics，Speech and Signal Processing. New Orleans，LA，USA：IEEE，2017：4845-4849.

4
Qiu J T， Wang J， Yao S，et al. Going deeper with embedded FPGA platform for convolutional neural network∥Proceedings of the 2016 ACM/SIGDA International Symposium on Field⁃Programmable Gate Arrays. New York：ACM Press，2016：26-35.

5
Zhao R Z， Niu X Y， Wu Y J，et al. Optimizing CNN⁃based object detection algorithms on embedded FPGA platforms∥13th International Symposium on Applied Reconfigurable Computing. Springer Berlin Heidelberg，2017：255-267.

6
仇越，马文涛，柴志雷. 一种基于FPGA的卷积神经网络加速器设计与实现. 微电子学与计算机，2018，35(8)：68-72，77.

Qiu Y， Ma W T， Chai Z L. Design and implementation of a convolutional neural network accelerator based on FPGA. Microelectronics & Computer，2018，35(8)：68-72，77.

7
陈辰，柴志雷，夏珺. 基于Zynq7000 FPGA异构平台的YOLOv2加速器设计与实现. 计算机科学与探索，2019，13(10)：1677-1693.

Chen C， Chai Z L， Xia J. Design and implementation of YOLOv2 acce⁃lerator based on Zynq7000 FPGA heterogeneous platform. Journal of Frontiers of Computer Science and Technology，2019，13(10)：1677-1693.

8
曾成龙，刘强. 面向嵌入式FPGA的高性能卷积神经网络加速器设计. 计算机辅助设计与图形学学报，2019，31(9)：1645-1652.

Zeng C L， Liu Q. Design of high performance convolutional neural network accelerator for embedded FPGA. Journal of Computer⁃Aided Design and Computer Graphics，2019，31(9)：1645-1652.

9
徐欣，刘强，王少军. 一种高度并行的卷积神经网络加速器设计方法. 哈尔滨工业大学学报，2020，52(4)：31-37.

Xu X， Liu Q， Wang S J. A highly parallel design method for convolutional neural networks accelerator. Journal of Harbin Institute of Technology，2020，52(4)：31-37.

10
Li F F， Zhang B， Liu B. Ternary weight networks. 2016，arXiv：1605.04711.

11
Zhou S C， Wu Y X， Ni Z K，et al. Dorefa⁃net：Training low bitwidth convolutional neural networks with low bitwidth gradients. 2018，arXiv：1606.06160.

12
Banner R， Hubara I， Hoffer E，et al. Scalable methods for 8⁃bit training of neural networks∥Proceedings of the 32nd International Conference on Neural Information Processing Systems. Montreal，Canada：NIPS，2018：5145-5153.

13
Das D， Mellempudi N， Mudigere D，et al. Mixed precision training of convolutional neural networks using integer operation. 2018，arXiv：1802.00930.

14
Deng L， Li G Q， Han S，et al. Model compression and hardware acceleration for neural networks：A comprehensive survey. Proceedings of the IEEE，2020，108(4)：485-532.

15
Lin Y J， Han S， Mao H Z，et al. Deep gradient compression：Reducing the communication bandwidth for distributed training. 2020，arXiv：1712.01887.

16
Han D， Lee J， Lee J，et al . A 141.4 mW low⁃power online deep neural network training processor for real⁃time object tracking in mobile devices∥2018 IEEE International Symposium on Circuits and Systems. Florence，Italy：IEEE，2018：1-5.

17
Zhao W L， Fu H H， Luk W，et al. F⁃CNN：An FPGA⁃based framework for training convolutional neural networks∥IEEE 27th International Conference on Application⁃specific Systems，Architectures and Processors. London，UK：IEEE，2016：107-114.

18
Liu Z Q， Dou Y， Jiang J F，et al. An FPGA⁃based processor for training convolutional neural networks∥2017 International Conference on Field Programmable Technology. Melbourne，Australia：IEEE，2017：207-210.

19
Fox S， Faraon J， Boland D，et al. Training deep neural networks in low⁃precision with high accuracy using FPGAs∥2019 International Conference on Field⁃Programmable Technology. Tianjin，China：IEEE，2019：1-9.

20
Luo C， Sit M K， Fan H X，et al. Towards efficient deep neural network training by FPGA⁃based batch⁃level parallelism. Journal of Semiconductors，2020，41(2)：022403.

Options
Outlines

/

〈 〉

Copyright © Journal of Nanjing University(Natural Sciences), All Rights Reserved.
Powered by Beijing Magtech Co. Ltd.